最近OpenAI太反常,消息一会一变,直让人摸不着头脑。
奥特曼最新宣布:5月13日开发布会,不是GPT-5,也不是盛传的GPT搜索引擎,改成对ChatGP和GPT-4的升级~

消息一出,大伙儿都蒙了。
之前大张旗鼓给SearchGPT搜索引擎造势,域名、前端界面都准备好了,甚至已经有用户收到灰度测试。
大有在谷歌I/O大会(5月14日)前狙击一把谷歌核心业务的架子,就像春节期间用Sora狙击了谷歌大模型Gemini 1.5一样。
再加上路透社啊、彭博社啊这些权威媒体也纷纷收到“消息人士”线报,结果刚把消息发出去,就被官方“打脸”了。

总之SearchGPT正把全球科技圈挠的心痒痒,然后突然没下文了??
事出反常必有妖。
知名OpenAI爆料者**@Flowers from the future**(花哥)透露,至少一位他和另一位爆料者**@Jimmy Apples**(苹果哥)的共同“线人”已经被开除了。

许多网友到这里才恍然大悟,用抓内鬼的视角来看,之前的种种离谱突然就合理了起来。
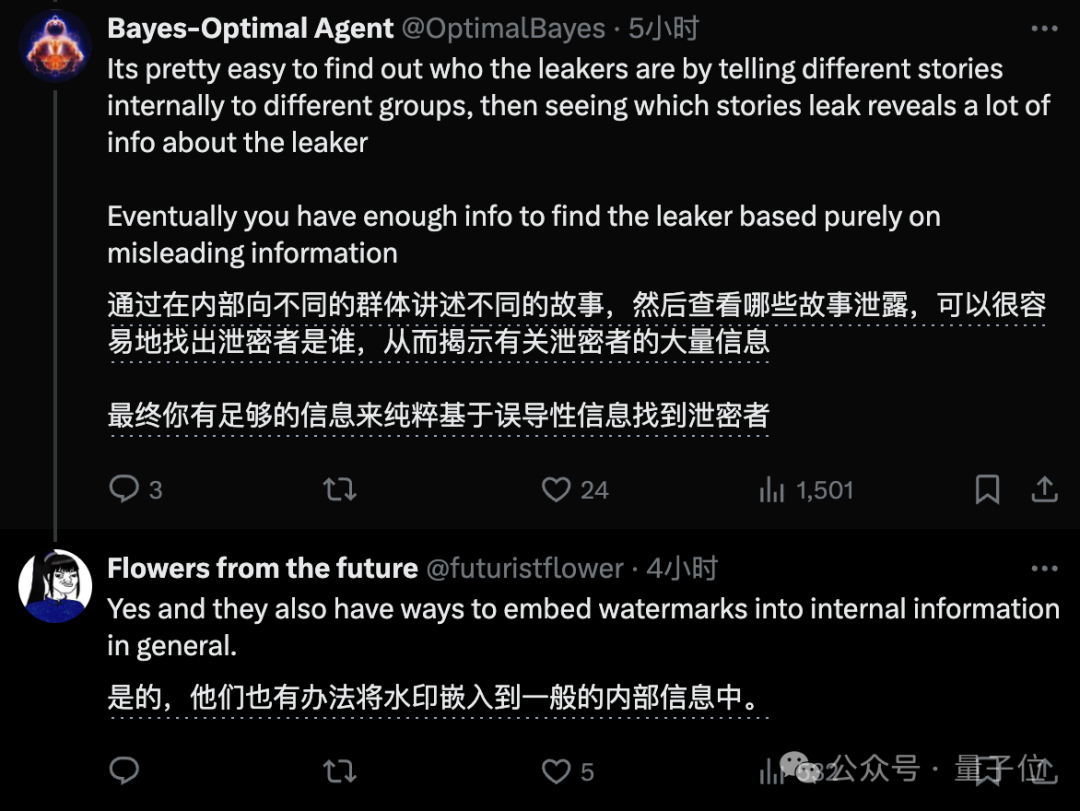
甚至有网友在10几天之前就猜出了这个套路,“就像在运行一个二分法搜索”。
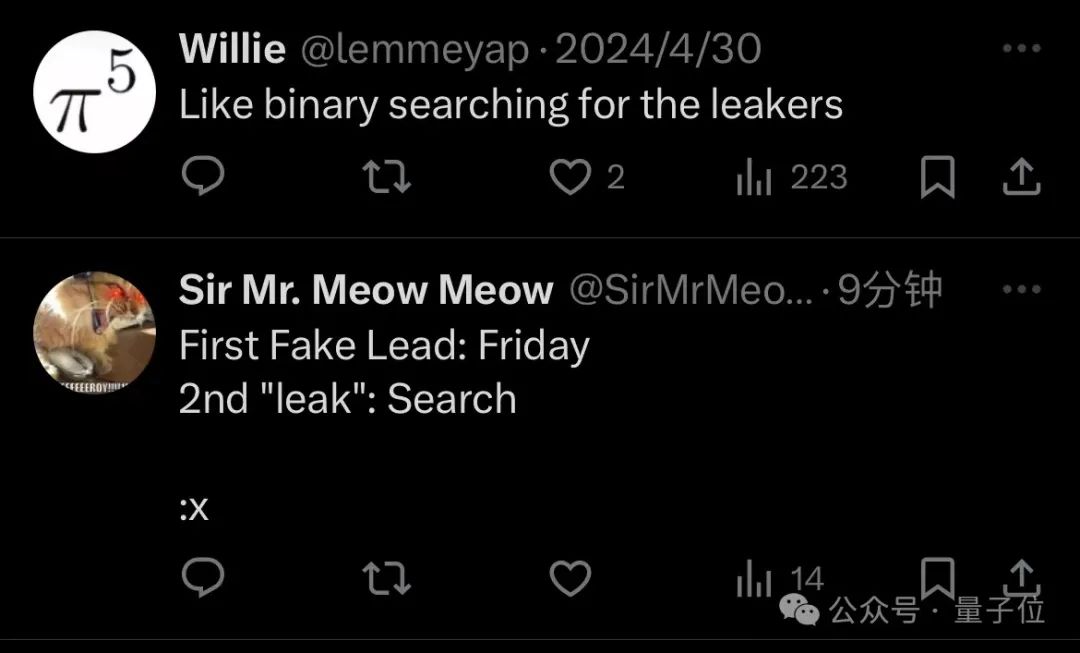
开除内鬼计划进行中
近期OpenAI人事变动很频繁,除了主动跳槽的,开除内鬼计划已经在进行中了。
除了花哥最新透露、还没有确切消息的这位,还有Ilya盟友、安全对齐研究员Leopold Aschenbrenner和Pavel Izmailov。
开除他们的理由正是泄密,可能与Q*相关。
其中Pavel Izmailov已经跳槽到马斯克旗下的xAI,明年也将成为纽约大学助理教授。

另一位Leopold的个人资料还未更新,目前动向不明。
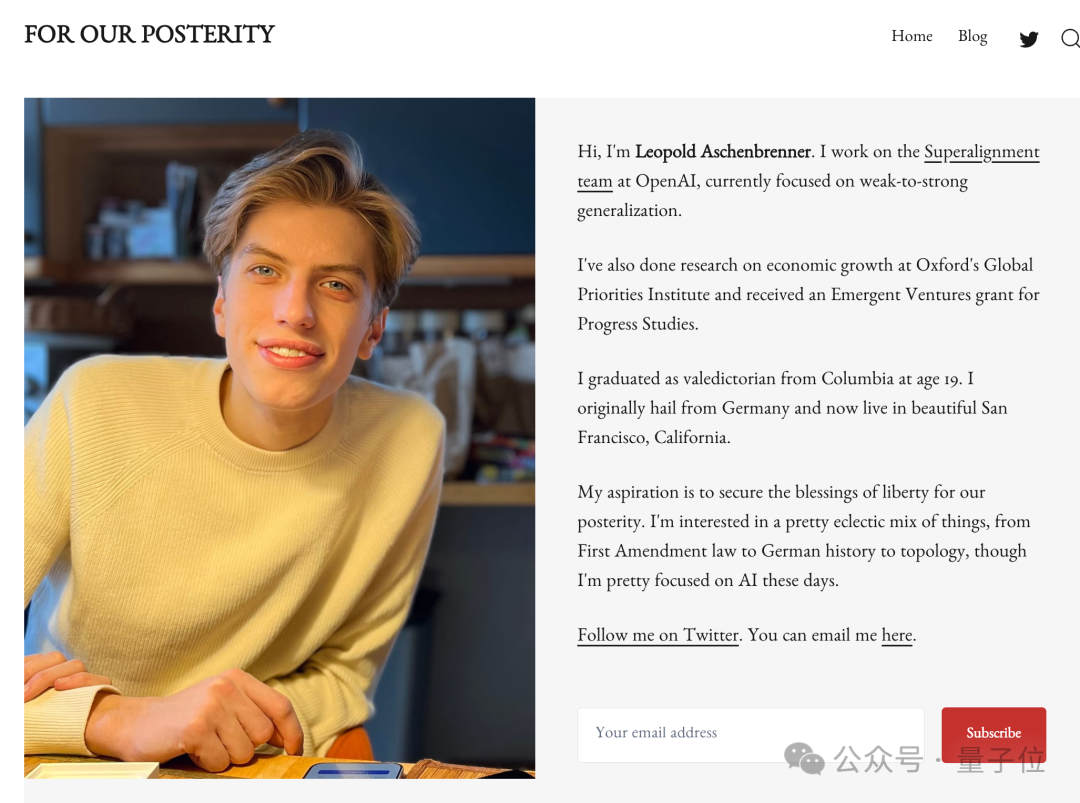
对于OpenAI安全对齐团队来说,最近半年人才流失严重,除了被开除的两位,也不乏主动离职的。
参与过GPT-4对抗性测试的Daniel Kokotajlo,Ilya领导的超级对齐团队的William Saunders,两人的离开都已获得证实。
其中Kokotajlo在Less Wrong论坛留下了自己的理由:
对OpenAI能否在AGI时代负责任的行动失去了信心。
按他的说法,当前的AI监管努力集中在“评估风险和采取缓解措施”的组合上,这种组合很容易被大型公司钻空子利用,最终导致“选择性暂停”。
也就是最需要被监管的前沿大型AI实验室反而没被监管到,对这种可能性的幻灭是他离开OpenAI的部分原因。
除此之外,近期OpenAI离职的还有人事副总裁Diane Yoon和非营利组织和战略计划负责人Chris Clark。
当然,OpenAI也在不断引进新鲜血液。
一位新加入的开发平台工程师表示,上班第一周就像一场旋风,一周内把模型部署到生产环境这个大流程就走了整整3次。
就直接一个好家伙,普通公司可能新手第一个月都在内部培训呢吧。

下周到底发什么?
不管抓内鬼是不是这一系列骚操作的原因之一,官方宣布直播线上发布会总不敢鸽掉(北京时间下周二凌晨1点)。
我们将演示ChatGPT和GPT4的一些升级。

从OpenAI员工们的反应来看,他们也正处在一个集体亢奋的状态,称新发布很酷,“比GPT-5还酷”


到底升级的是什么,说法可就五花八门喽,我们筛选了想读靠谱的几个说法供大家参考:
- 语音助手
根据科技媒体The Information消息,OpenAI正在开发一种新的AI语音助手。
与Siri或ChatGPT语音模式不同,新技术可以理解人类声音中的语气、比如提问时是否在讽刺。
除此之外还拥有更好的推理能力,在某些任务上甚至击败了GPT-4 Turbo。
这项技术让不少人想起电影《她》中的AI伴侣萨曼莎,事实上过去奥特曼也多次表示《她》是他本人最喜欢的AI主题电影。

- GPT-4轻量级版
有人从ChatGPT安卓版安装包1.2024.122版本中发现了三个新的模型名称。
gpt-4l,gpt-4l-auto,gpt-4-auto。
其中“l”很可能指“lite”,也就是轻量版,在SearchGPT前端代码中也有提到。
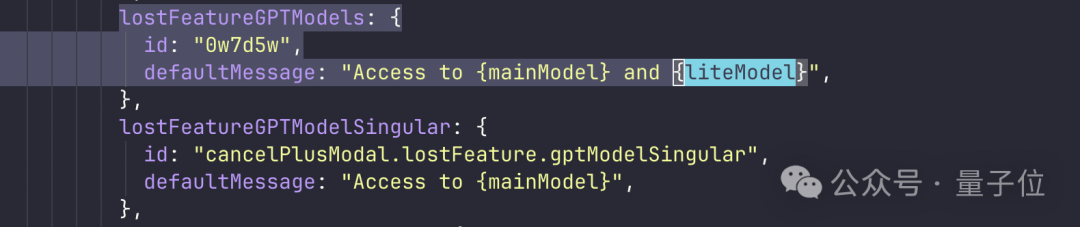
而auto则可能指动态选择,根据提示词难度自动为用户在更强的模型和更快的模型之间做平衡。

- 大量Agents应用
一种并没有直接消息来源,但也很流行的猜测是将发布大量Agents应用。
理由是奥特曼前不久在MIT的活动上称Agents将成为AI的杀手级功能。

- 与苹果合作
来自彭博社的消息指出,苹果接近与OpenAI达成合作协议,将以某种形式将ChatGPT引入iPhone手机。
不过正式消息更可能在6月份的苹果WWDC上宣布,也就是作为iOS 18的新特性。

总之,现在很多人的心情be like:

以及这个周末会感觉很漫长。
下周二凌晨,量子位将第一时间带来最新消息。
在等待的功夫,不妨在评论区留下你的看法,你认为OpenAI下周二会发布什么?
参考链接:
[1]https://x.com/sama/status/1788989777452408943
[2]https://www.businessinsider.com/openai-safety-researchers-quit-superalignment-sam-altman-chatgpt-2024-5
[3]https://x.com/btibor91/status/1788646471580934358










064:添加字符065:数组变换066:装箱问题](https://img-blog.csdnimg.cn/direct/6dc326485bb246f2bb9225f22ce39a23.png)