可能需要:MySQL下载–》更新版本–》迁移数据库到MySQL
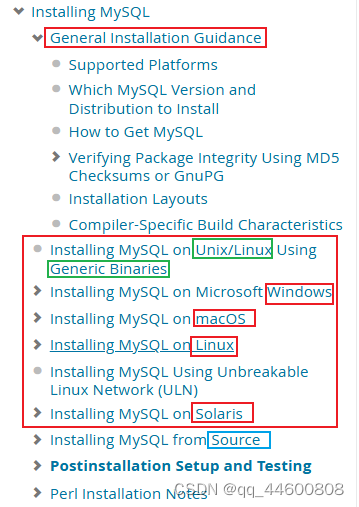
以下都不重要【只要确定好需要安装版本,找到对应的版本下载,安装,设置即可】
下载、安装:
- Determine whether MySQL runs and is supported on your platform.
支持的平台 - Choose which track to install.
- bugfix track
- innovation track
- Choose which track to install.
- Download the distribution that you want to install.【下载二进制版本、源代码版本】、【下载地址】
- Install the distribution.
- Perform any necessary postinstallation setup.
- If you want to run the MySQL benchmark scripts, Perl support for MySQL must be available. 【基准测试脚本–》Perl】
前3步都是在选择版本,4、5步在进行下载,6安装前配置