图搜索算法-最短路径算法-贝尔曼-福特算法

news2025/1/18 9:04:36

相关文章：
数据结构–图的概念
图搜索算法 - 深度优先搜索法（DFS）
图搜索算法 - 广度优先搜索法（BFS）
图搜索算法 - 拓扑排序
图搜索算法-最短路径算法-戴克斯特拉算法

贝尔曼-福特算法（Bellman-Ford）

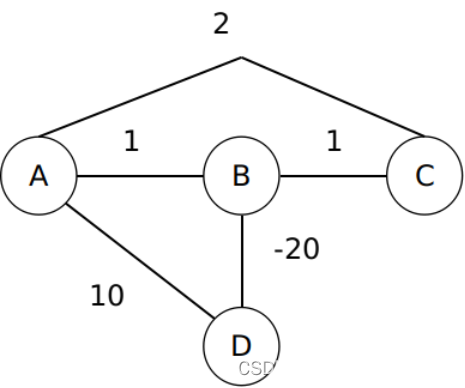
现在继续学习求解最短路径的第二种算法，首先回想戴克斯特拉算法的例子，每个边的权重都是正整数，若出现负权重，算法能不能正常运行呢？看以下例子，如图所示。
在这里插入图片描述

# 运行戴克斯特拉算法
g = DijkstraGraph(['A','B','C','D']) 
g.graph = [[0, 1, 2, 10], 
        [1, 0, 1, -20], 
        [2, 1, 0, 0], 
        [10, -20, 0, 0],
        ]; 
g.dijkstra(0)# A作为源结点
#-------------结果----------------
结点      距离源结点的距离
A        0
B        1
C        2
D        10

结果明显是错误的，大家清楚知道结点【B】到结点【A】最短距离不是1，它可以通过结点【D】到结点【A】，此时最短距离为-10，而且如果能够循环，每次循环距离还能不断缩小，变成一个死循环。既然戴克斯特拉算法没有办法计算负权重问题，那有什么算法可以呢？所以第二个算法正是能够处理此类问题，它叫贝尔曼-福特（Bellman–Ford）算法。

贝尔曼-福特算法最大特点是支持负权重的情况，它每次都会从源结点重新出发对每一个结点进行距离计算并更新最小距离，而戴克斯特拉算法是从源结点出发向外扩逐个处理相邻的结点，不会去重复处理结点，从这也可以知道戴克斯特拉算法相对更高效一点。现在通过一个简单例子，来观察贝尔曼-福特算法处理过程，例子如下图所示。
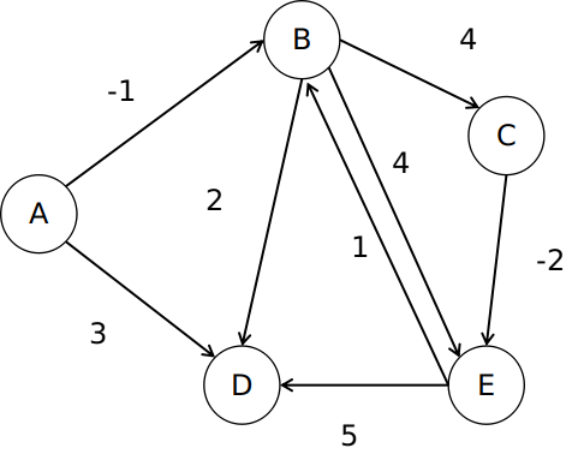
在这里插入图片描述
（1）这次要处理的是有权有向图，因此图的表示方式使用邻接列。首先初始化【distance】列表，结点【A】为源结点，它和自身的距离为0，其余结点到源结点的距离为无穷大（∞），那么【distance】值为【0,∞,∞,∞,∞】，如图所示。
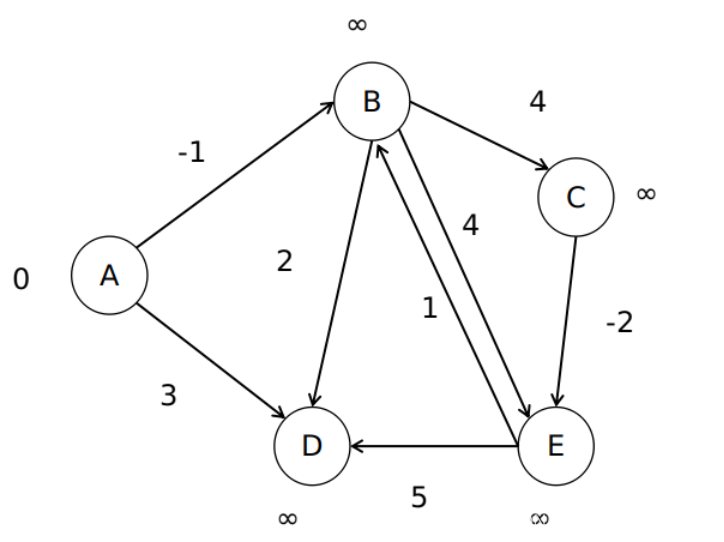
在这里插入图片描述
（2）每一轮要计算每一个结点到源结点的距离，一共要经过N-1轮边距离松弛（N为结点数），因为结点到源结点若连通，最多就是N-1条边就可以达到。第一轮计算结点【A】一条边能到达的结点，计算过程如表所示。
在这里插入图片描述
（3）根据上表得知，现在【distance】值为【0,-1,∞,3,∞】。然后到第二轮，计算结点【A】两条边能到达的结点，计算过程如表所示。

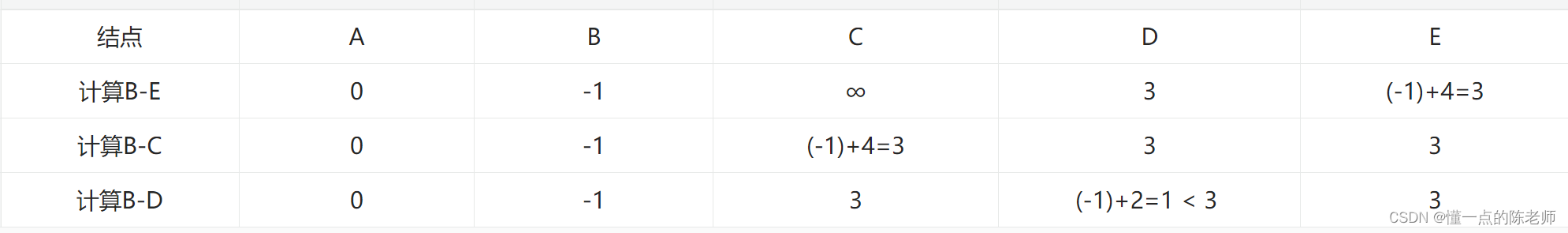
（4）根据上表得知，现在【distance】值为【0,-1,3,1,3】。然后到第三轮，计算结点【A】三条边能到达的结点，计算过程如表所示。
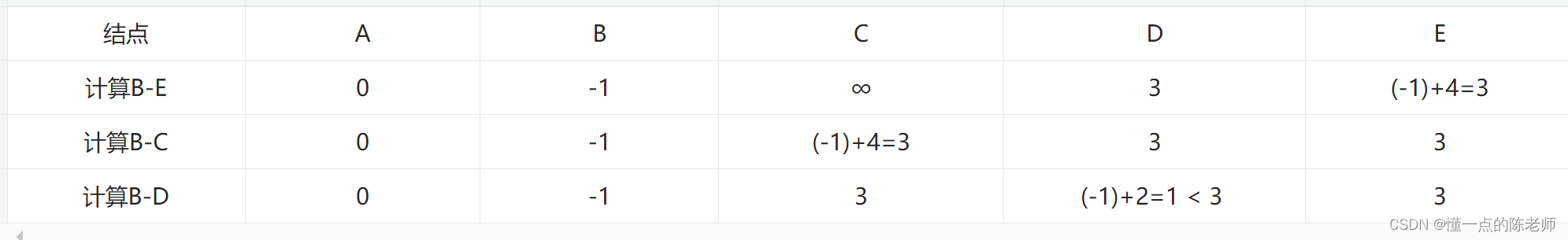
在这里插入图片描述
（5）根据上表得知，现在【distance】值为【0,-1,3,1,1】。然后到第四轮，由于结点数为5，因此这是最后一轮（5-1=4），计算结点【A】四条边能到达的结点，计算过程如表所示。

（6）根据上表得知，现在【distance】值为【0,-1,3,1,1】，最终结果如图所示。
在这里插入图片描述
从上面运算过程可知贝尔曼-福特算法要遍历每一个结点，每次要对所有边进行松弛操作，所以时间复杂度为O(N*E)，N为结点数，E为边数。在空间上只需要【distance】来记录结果，因此空间复杂度为O(N)。

现在要用代码来表现上面的过程，首先这是一个有权有向图，可以创建【GraphPower】类来表示。然后创建【GraphBellmanFord】继承【GraphPower】类可以录入邻接列表，bellman_ford()函数是算法的主程序，其中用一个列表【distance】记录每个结点到源结点的距离，print_result()函数格式化输出结果。

class GraphPower(): 
    """有权图类"""
    def __init__(self, points):
        self.amount = len(points) # 记录结点的总数
        self.points = points      # 记录结点位置和值的关系
        self.graph = []           #  初始化图的邻接列表
    def add_edge(self, u, v, w):
        if u in self.points and v in self.points:
            index_u = self.points.index(u)
            index_v = self.points.index(v)
            self.graph.append([index_u, index_v, w]) # 录入数据
        else:
            print("录入数据有误")

class GraphBellmanFord(GraphPower):
    """贝尔曼-福特（Bellman–Ford）算法"""
    def print_result(self, dist): 
        print("结点到源结点的距离：") 
        for i in range(self.amount): 
            print("{} \t {}".format(self.points[i], dist[i])) 
    def bellman_ford(self, source):
        """主程序贝尔曼福特算法求每个结点到源结点最短路径，并且检查是否有负循环"""
        # 第一步：初始化参数，所有结点到源结点的距离为正无穷大 
        distance= [float("Inf")]*self.amount # float("Inf")为正无穷大
        distance[source] = 0  # 源结点本身距离为0
        # 第二步: 进行N-1次的边松弛，找结点到源结点的最短距离
        for i in range(self.amount - 1):
            for u, v, w in self.graph:
                # distance(a) +weight(ab)) < distance(b) 说明存在有更短路径从a到b。
                if distance[u] != float("Inf") and distance[u] + w < distance[v]: 
                        distance[v] = distance[u] + w # 更新最短路径
        # 第三步: 检查是否存在负循环,在完成这么N-1次松弛后如果还是可以松弛（找到更短路径）的话说明存在负循环
        for u, v, w in self.graph:
            if distance[u] != float("Inf") and distance[u] + w < distance[v]: 
                    print("图包含负循环")
                    return
        self.print_result(distance) # 打印结果

以例子为输入，来测试程序。

g = GraphBellmanFord(['A','B','C','D','E']) # 初始化图，记录结点值
g.add_edge('A','B', -1) # 添加边
g.add_edge('A','D', 3) 
g.add_edge('B','D', 2)
g.add_edge('B','C', 4)
g.add_edge('B','E', 4)
g.add_edge('C','E', -2)
g.add_edge('E','B', 1)
g.add_edge('E','D', 5)
g.bellman_ford(0) # 按结点A为源结点计算结点的最短距离
#-------------------结果------------------------
结点到源结点的距离：
A        0
B        -1
C        3
D        1
E        1