在 C++ 中,std::complex 是一个模板类,用于表示和操作复数。这个类是标准模板库(STL)的一部分,包含在 头文件中。std::complex 提供了一套丰富的功能,包括基本的算术运算、比较运算、数学函数等,使得处理复数成为一件简单而直接的事情。
#include <iostream>
#include <complex>
int main() {
// 创建两个复数
std::complex<double> num1(2.0, 3.0); // 2 + 3i
std::complex<double> num2(3.0, 4.0); // 3 + 4i
// 复数的加法
std::complex<double> sum = num1 + num2;
std::cout << "Sum: " << sum << std::endl;
// 复数的乘法
std::complex<double> prod = num1 * num2;
std::cout << "Product: " << prod << std::endl;
// 复数的除法
std::complex<double> quotient = num1 / num2;
std::cout << "Quotient: " << quotient << std::endl;
// 复数的共轭
std::complex<double> conjugate = std::conj(num1);
std::cout << "Conjugate of num1: " << conjugate << std::endl;
// 获取复数的模(绝对值)
double absValue = std::abs(num1);
std::cout << "Absolute value of num1: " << absValue << std::endl;
// 获取复数的相位(角度)
double phase = std::arg(num1);
std::cout << "Phase of num1: " << phase << std::endl;
// 获取复数的实部和虚部
double realPart = num1.real();
double imagPart = num1.imag();
std::cout << "Real part: " << realPart << ", Imaginary part: " << imagPart << std::endl;
return 0;
}
主要函数和操作
- 构造函数:std::complex z(a, b); 其中 a 是实部,b 是虚部,T 可以是 float、double 或 long double。
- 算术运算符:支持 +, -, *, / 以及与实数的组合运算。
- 共轭:std::conj(z) 返回复数 z 的共轭。
- 绝对值/模:std::abs(z) 返回复数 z 的模。
- 相位/角度:std::arg(z) 返回复数 z 的相位(角度)。
- 实部和虚部:z.real() 和 z.imag() 分别获取复数的实部和虚部。
- 指数、对数、幂和平方根:函数如 std::exp,std::log, std::pow 和 std::sqrt 也可以用于复数。
std::complex求逆
在 C++ 中,使用 std::complex 类型时,求一个复数的逆(或倒数)并不直接提供为一个单独的函数。然而,可以通过使用已有的运算符和函数来计算一个复数的逆。
求复数逆的公式
复数 z=a+bi 的逆可以通过以下公式计算:
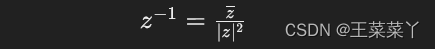
#include <iostream>
#include <complex>
int main() {
std::complex<double> z(2, 3); // 定义一个复数 2+3i
// 计算逆
std::complex<double> inverse_z = std::conj(z) / std::norm(z);
std::cout << "Complex number: " << z << std::endl;
std::cout << "Inverse of the complex number: " << inverse_z << std::endl;
return 0;
}
关键函数
std::conj(z):计算复数 z 的共轭。
std::norm(z):计算复数 z 的模的平方,等同于 ∣z∣2。
使用除法 / 运算符来除以模的平方,得到逆。
注意
上面的代码计算了复数的逆,这适用于非零复数。
如果尝试求零复数的逆,将会遇到除以零的错误。
在实际应用中,应当检查复数是否为零,避免运行时错误。
std::norm(z) 返回的是模的平方,而不是模本身。如果需要模本身,则可以使用 std::abs(z),但在这里直接使用模的平方是计算逆的一个更高效的方法,因为它避免了求平方根的开销。