题目描述

        一条直线上有 𝑛 个信使，将他们按照从左至右的顺序以 1 至 𝑛 编号。换句话说，设 𝑖 号信使的的坐标为 𝑑𝑖​，则对于 1≤𝑖<𝑛， 𝑑𝑖≤𝑑𝑖+1​。

    信使传递一条消息的方法如下：

• 在任意时刻（不一定是整数时刻），任一信使（无论是否已知消息）都可以自由选择向左移动或者向右移动或者原地不动。其移动的速度为每秒 1 单位长度。
• 当两个信使相距不超过一给定实数 𝑘 时，双方可以进行消息传递，也即如果两人中有一人已知该消息，则两人都知道了该消息。消息传递是瞬间发生的，不消耗时间。

现在 1 号信使得到了一条消息，请求出最小的让所有信使都得到该消息的用时。

分析

        题解区中的大佬貌似基本上用的都是二分，所以来写一篇（可能会被hack的）贪心

        首先考虑只有2个人的时候，显然是两个人同时往中间走，到距离为k的时候停下最优。                  当人数增加的时候，由于每个人相互之间不会影响，所以前面的人向前移动传递消息，就可以看做把整个系列向前移动，对后续传递是不会又影响的。

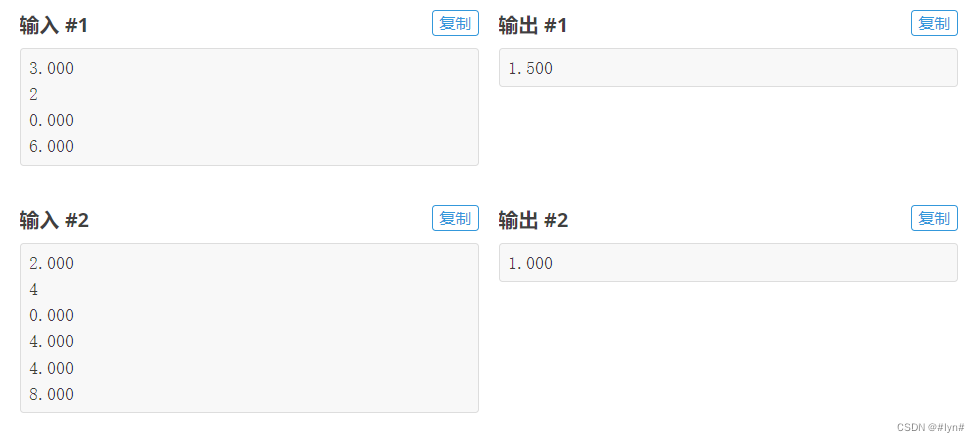
        但通过观察样例2，不难发现，存在前一个信使往前移动，且后一个不动的情况下依然可以满足距离小于k的情况。此时，后一个信使就可以在满足距离小于k的条件下向后移动，这样可以缩小该信使与他的下一个之间的距离，一定不会更劣。

        所以整个传递的过程就是一个线性，不断往后推的过程

                【能 HACK 掉的大佬请私我】

Code

        

#include<bits/stdc++.h>
using namespace std;
int n;
double k,x,t,d[100005];
int main()
{
 	scanf("%lf%d",&k,&n);
 	for(int i=1;i<=n;i++) scanf("%lf",d+i);
 	if(n==1) { cout<<0; return 0; }
 	t=max(0.0,(d[2]-d[1]-k)/2.0); d[2]-=t;
 	for(int i=3;i<=n;i++)
 	{
 		if(d[i-1]+k>=d[i]) { d[i]=min(d[i-1]+k,d[i]+t); continue; }
 		if(d[i-1]+k+t>=d[i]) { d[i]=d[i-1]+k; continue; }
 		d[i]-=t; x=(d[i]-d[i-1]-k)/2.0,d[i]-=x,t+=x;
	}
	printf("%.4lf",t);
	return 0;
}