一 、 贪心算法的解题套路实战一(最多的会议宣讲场次)
1.1 描述
一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。
给你每一个项目开始的时间和结束的时间
你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。
返回最多的宣讲场次。
1.2 分析 在绝对环境下选择最优解
贪心 先按会议结束时间排序,然后在在数组里面找,先以前开始时间为0,找第一个会议可以结束的时间更新会议下一个可以开始的时间为当前这个会议的结束时间,那么下一个会议可以开始的时间要大于前面那个结束的时间
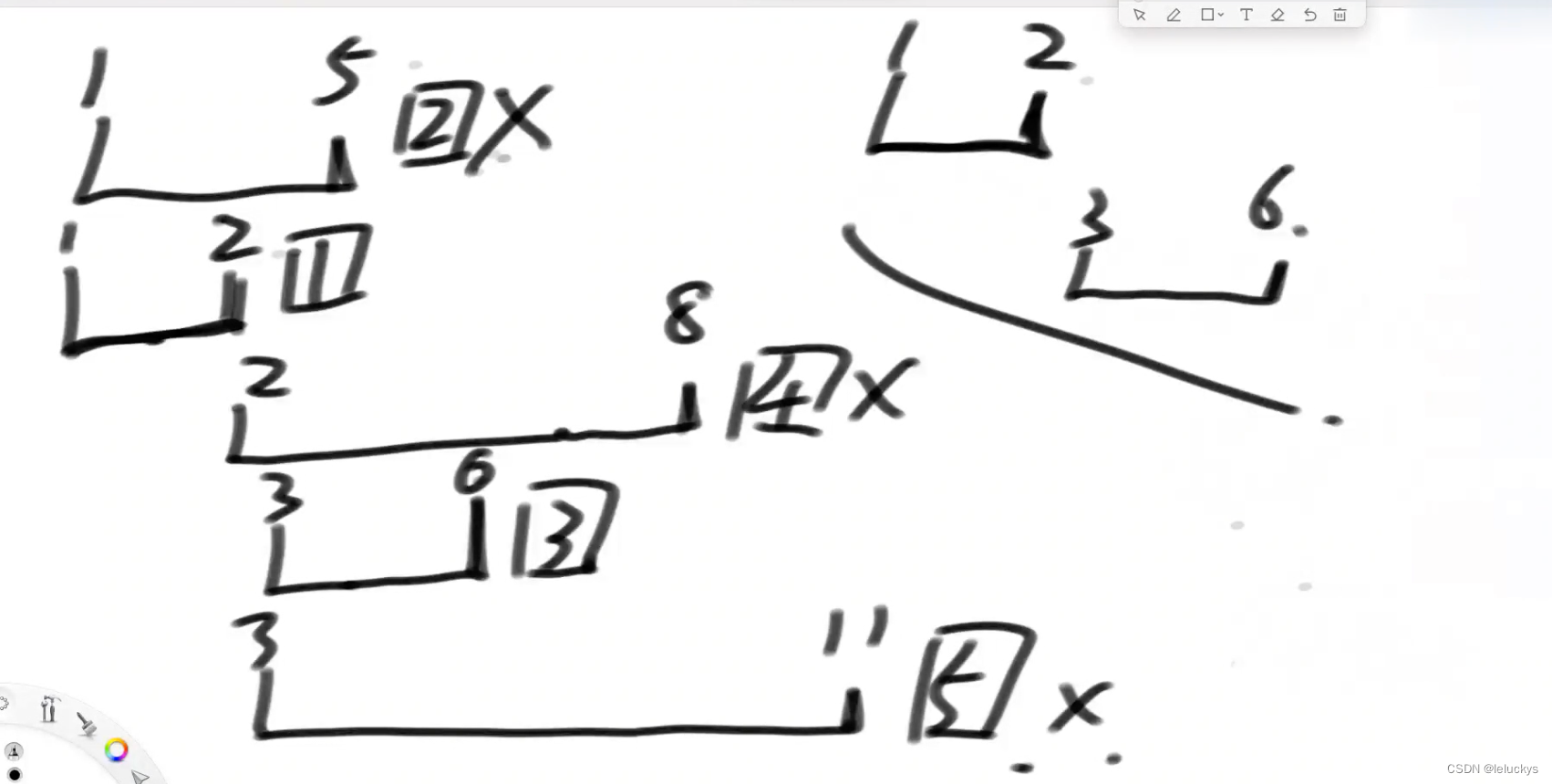
1.3 代码
// 会议的开始时间和结束时间,都是数值,不会 < 0
public static int bestArrange2(Program[] programs) {
Arrays.sort(programs, new ProgramComparator());
int timeLine = 0;//会议的默认结束时间
int result = 0;
// 依次遍历每一个会议,结束时间早的会议先遍历
//比如上一个会议的结束时间比下一个会议的开始时间小,那么下一个会议就可以在上一个会议结束的时候开始
for (int i = 0; i < programs.length; i++) {
if (timeLine <= programs[i].start) {
result++;
timeLine = programs[i].end;
}
}
return result;
}
//比较器
public static class ProgramComparator implements Comparator<Program> {
@Override
public int compare(Program o1, Program o2) {
return o1.end - o2.end;
}
}二 、 贪心算法的解题套路实战二(分割的最小代价)
2.1 描述
一块金条切成两半,是需要花费和长度数值一样的铜板的。
比如长度为20的金条,不管怎么切,都要花费20个铜板。 一群人想整分整块金条,怎么分最省铜板?
例如,给定数组{10,20,30},代表一共三个人,整块金条长度为60,金条要分成10,20,30三个部分。
如果先把长度60的金条分成10和50,花费60;
再把长度50的金条分成20和30,花费50;
一共花费110铜板。
但如果先把长度60的金条分成30和30,花费60;再把长度30金条分成10和20, 花费30;一共花费90铜板。
输入一个数组,返回分割的最小代价。
2.2 分析
贪心算法解决输入一个数组返回金条分割的最小代价既哈夫曼树
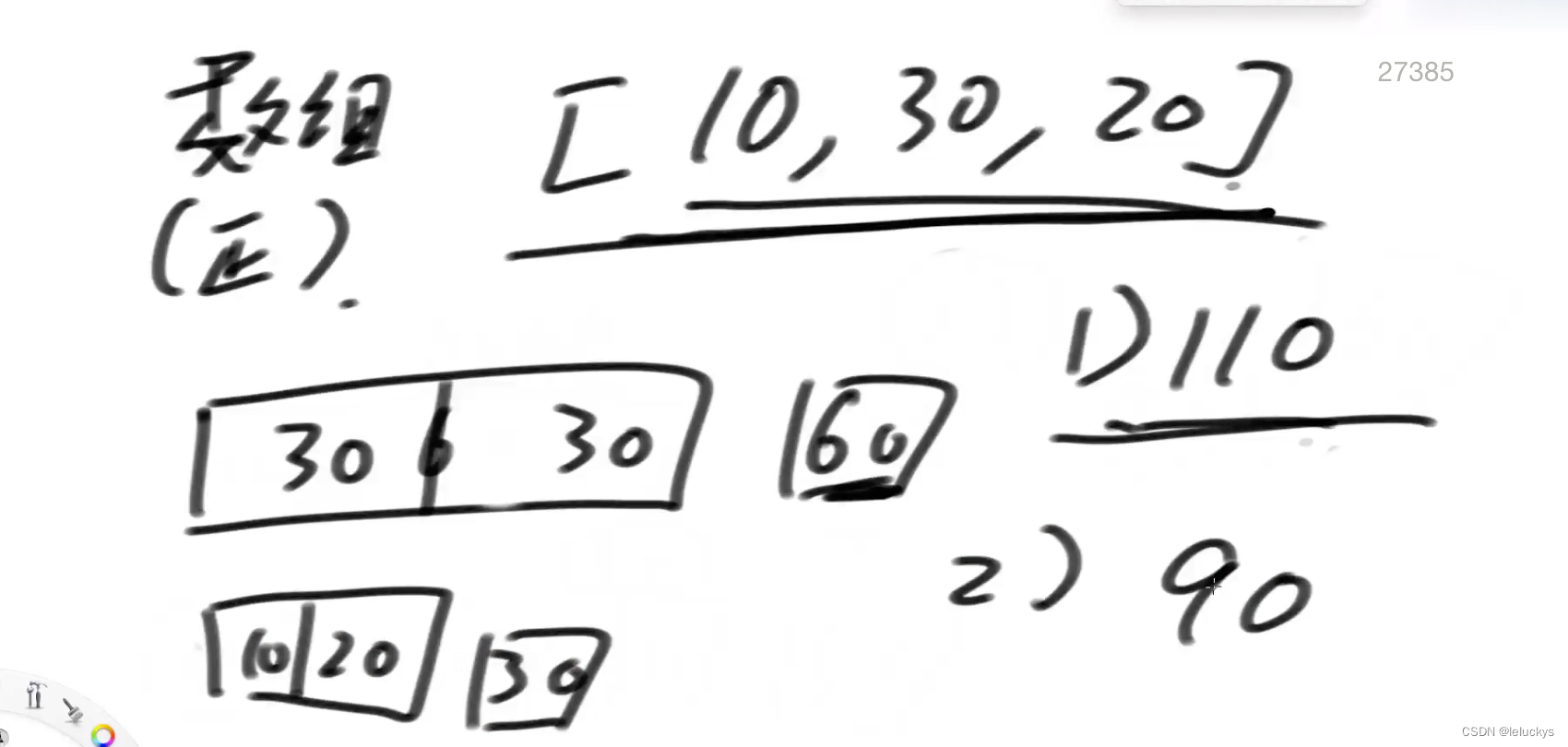
分析
根据上面的列子可以看出,切的时候尽可能的向平均靠近,之后的切的代价就越小
流程 使用小跟堆,每次从堆里面弹出两个树合完放入小根堆,等堆排好序后又弹出两个树,当小跟堆里面只剩一个树的时候停止,形成如下的树的方案就是最优方案,代价就是圈里面的值加起来-这就是在创建一棵哈夫曼树!
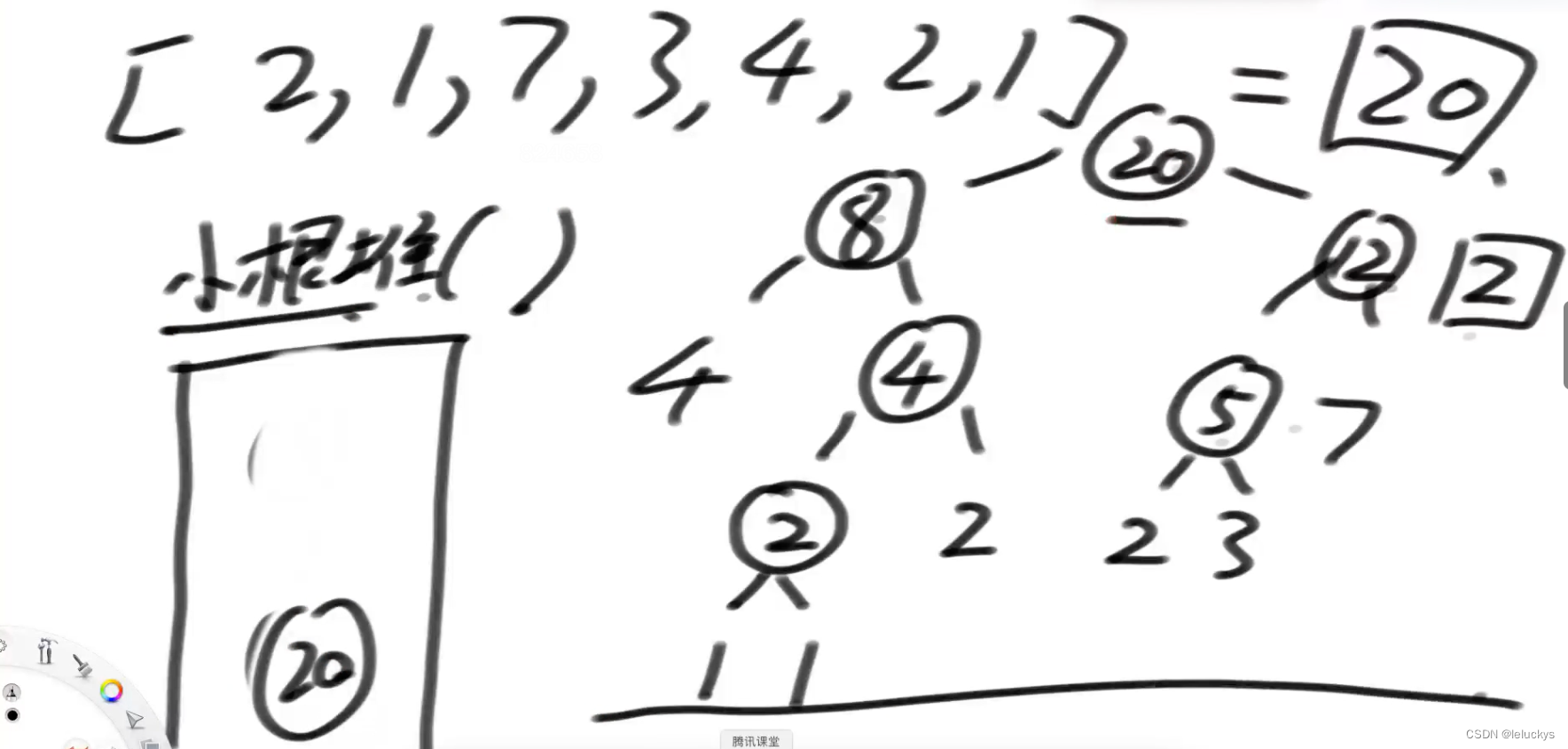
2.3 代码
public static int lessMoney2(int[] arr) {
PriorityQueue<Integer> pQ = new PriorityQueue<>();
for (int i = 0; i < arr.length; i++) {
pQ.add(arr[i]);
}
int sum = 0;
int cur = 0;
while (pQ.size() > 1) {
cur = pQ.poll() + pQ.poll();
sum += cur;
pQ.add(cur);
}
return sum;
}三 贪心算法的解题套路三 (根据下面的描述你最后获得的最大钱数)
3.1 描述
输入: 正数数组costs、正数数组profits、正数K、正数M
costs[i]表示i号项目的花费
profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润)
K表示你只能串行的最多做k个项目
M表示你初始的资金
说明: 每做完一个项目,马上获得的收益,可以支持你去做下一个项目。只能窜行的做项目,不能并行的做项目。
输出:你最后获得的最大钱数。
3.2 分析
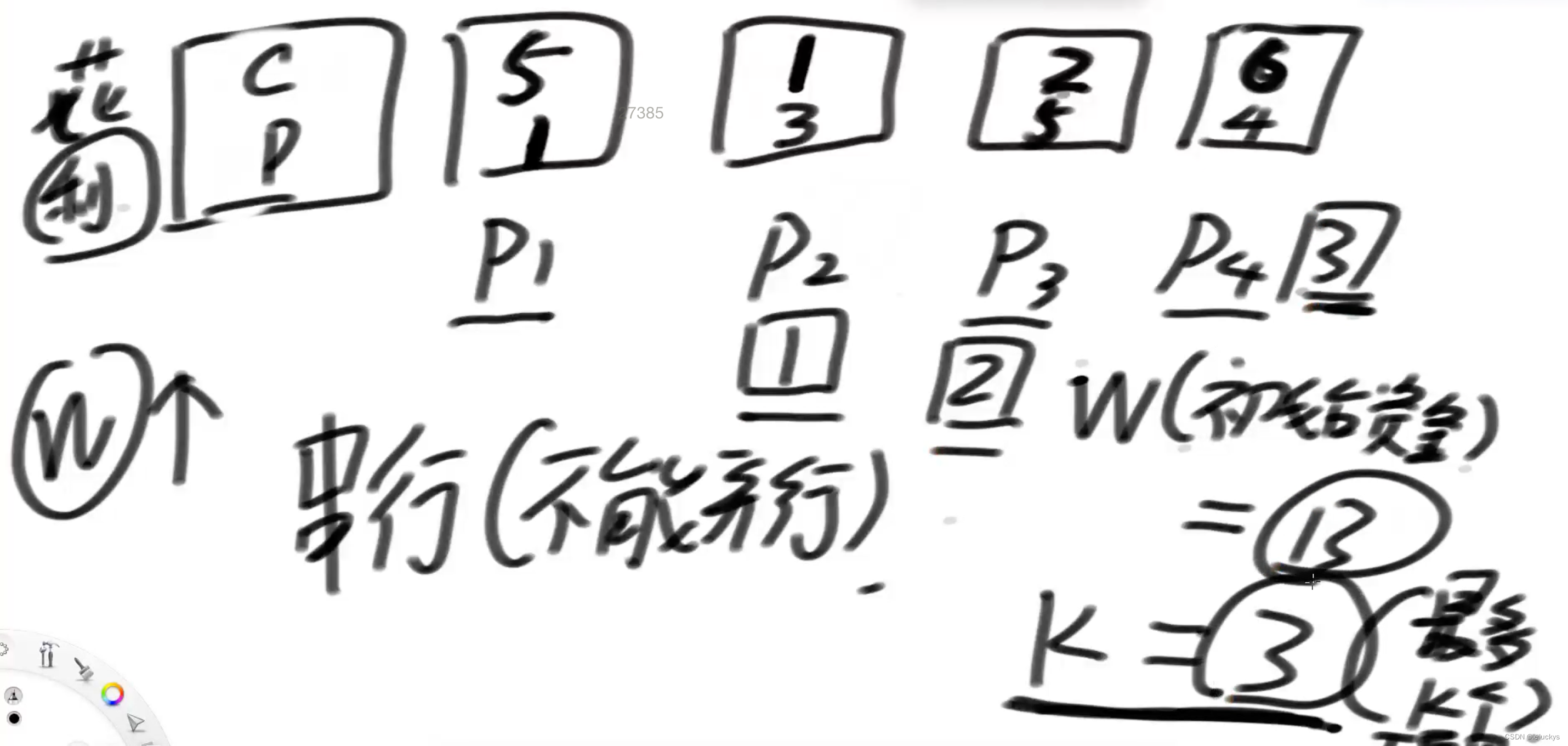
第一步 第一轮
分析先把所有数据按照花费放到小根堆里面,然后再来一个大根堆,按照利润来组织;假如我的钱是2元,小根堆里面所有能做的项目弹出来进大根堆;(1,3)(2,5)弹出进大根堆在大根堆里面是(2,5)(1,3)这个时候做要做的项目就是大根堆的堆顶;这个时候的利润就是2(本金)+5(利润)=7,
第二轮来了,接着第一轮的过程,从小根堆里面弹出7元能做的项目到大根堆里面;
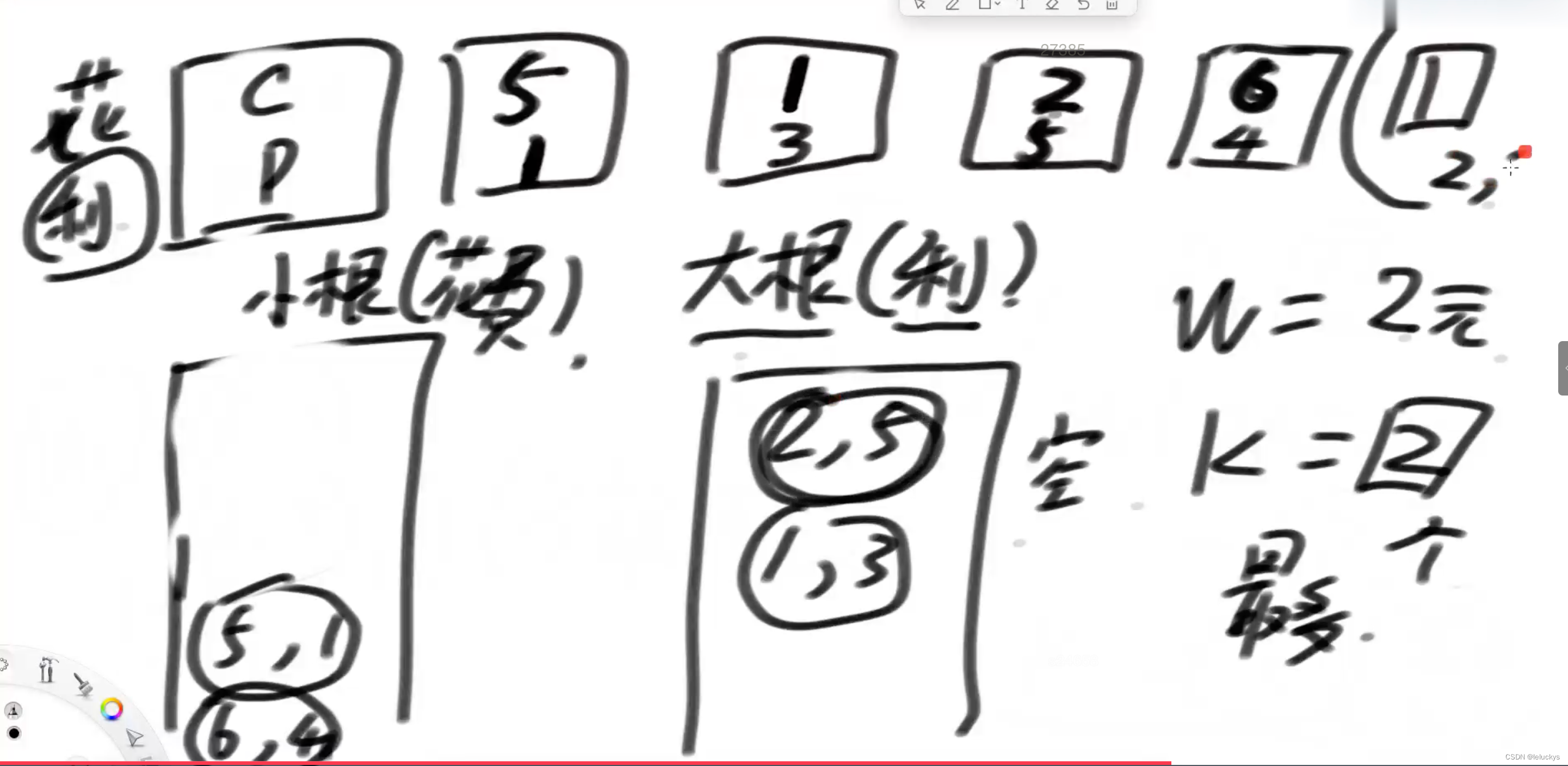
第二轮
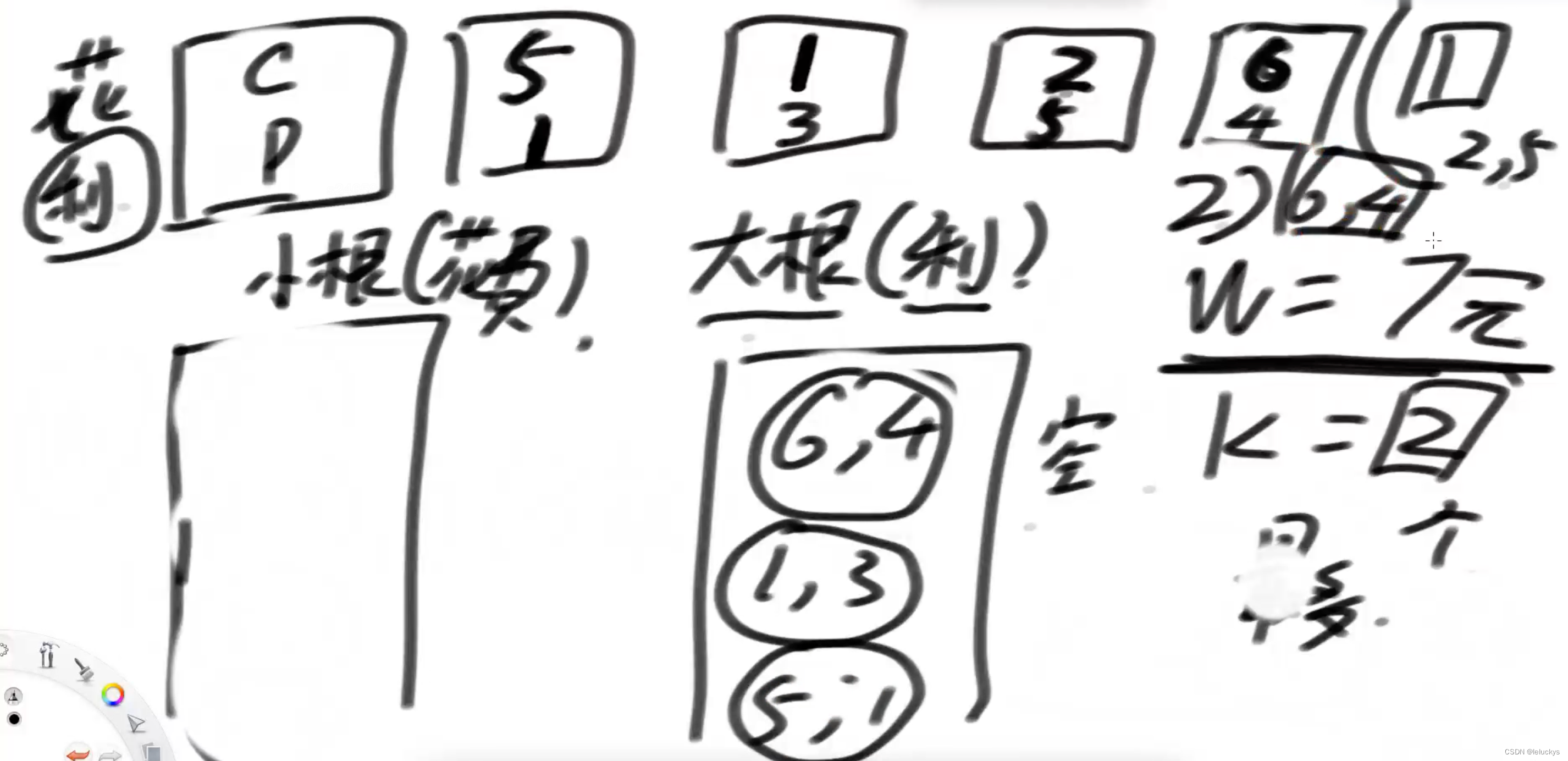
根据钱数去解锁小根堆,到大根堆做堆顶的树,一直循环

3.3 代码
package class14;
import java.util.Comparator;
import java.util.PriorityQueue;
public class Code04_IPO {
// 最多K个项目
// W是初始资金
// Profits[] Capital[] 一定等长
// 返回最终最大的资金
public static int findMaximizedCapital(int K, int W, int[] Profits, int[] Capital) {
PriorityQueue<Program> minCostQ = new PriorityQueue<>(new MinCostComparator());
PriorityQueue<Program> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
for (int i = 0; i < Profits.length; i++) {
minCostQ.add(new Program(Profits[i], Capital[i]));
}
for (int i = 0; i < K; i++) {
while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {
maxProfitQ.add(minCostQ.poll());
}
if (maxProfitQ.isEmpty()) {
return W;
}
W += maxProfitQ.poll().p;
}
return W;
}
public static class Program {
public int p;
public int c;
public Program(int p, int c) {
this.p = p;
this.c = c;
}
}
public static class MinCostComparator implements Comparator<Program> {
@Override
public int compare(Program o1, Program o2) {
return o1.c - o2.c;
}
}
public static class MaxProfitComparator implements Comparator<Program> {
@Override
public int compare(Program o1, Program o2) {
return o2.p - o1.p;
}
}
}
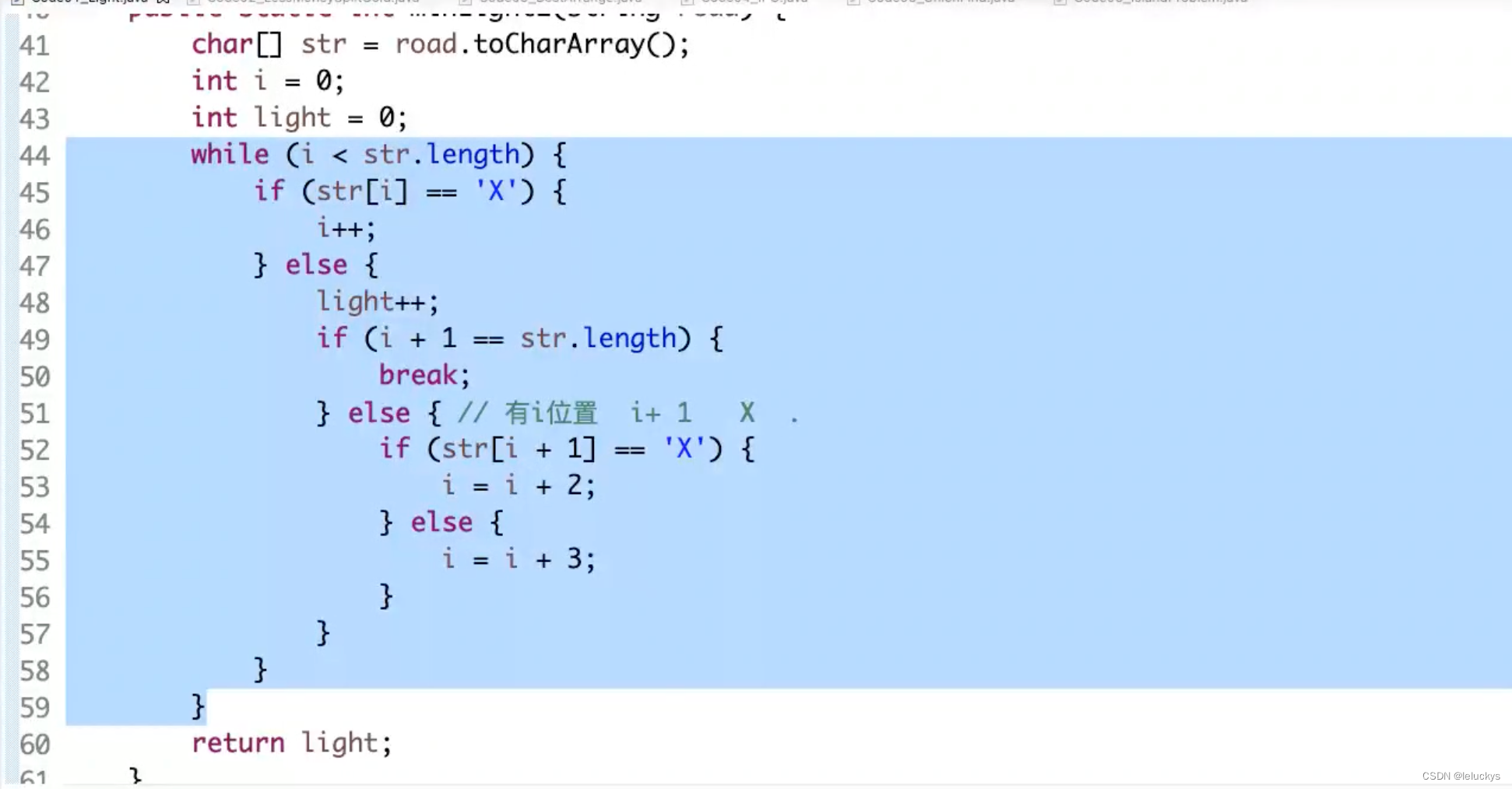
四 墙 路问题,需要多少灯
4.1 描述
给定一个字符串str,只由‘X’和‘.’两种字符构成。
‘X’表示墙,不能放灯,也不需要点亮
‘.’表示居民点,可以放灯,需要点亮
如果灯放在i位置,可以让i-1,i和i+1三个位置被点亮
返回如果点亮str中所有需要点亮的位置,至少需要几盏灯

4.1 分析

4.2 代码