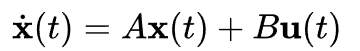
若在阅读过程中有些知识点存在盲区,可以回到如何优雅的谈论大模型重新阅读。另外斯坦福2024人工智能报告解读为通识性读物。若对于如果构建生成级别的AI架构则可以关注AI架构设计。技术宅麻烦死磕LLM背后的基础模型。
Mamba自从出道就一直被拿来和Transformer对比,文章巨多,带着标题的爆炸性字样“颠覆Transfomer”,“全面包围”等等。文章深浅不一,小编认为其背后的设计思路以及演化过程更加重要。为此本专题将从山上有座庙开始,沿着RNN、SSM、S4、HIPPO一路走来。期间抛弃冗杂的文辞,以更接地气的模式协助读者打开新的逻辑思维。

1分钟读完本文
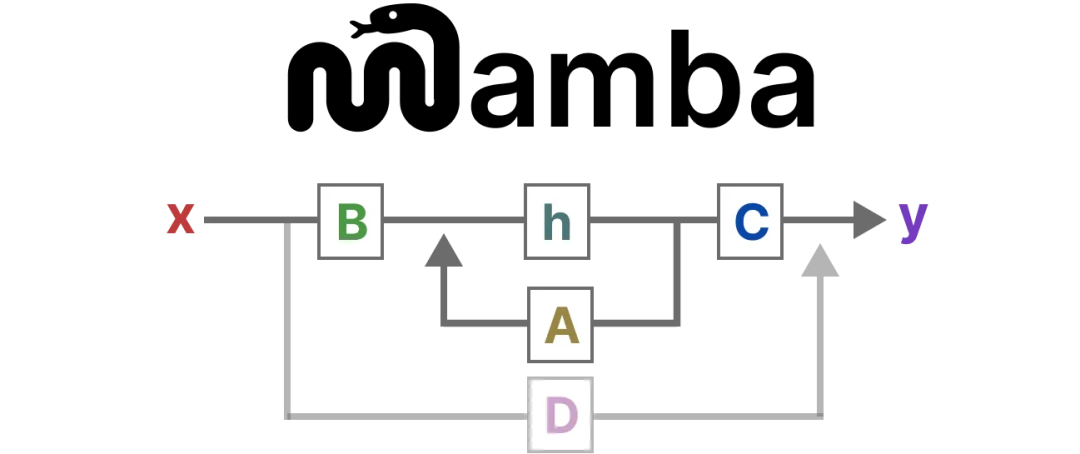
接着Mamab3的话题,带领着读者们梳理一下前情回顾。SSM接受一组连续的信号,然后吐出对应的输出信号。中间的黑盒子基于输入信号和上一时刻的状态进行某种变换而得到新的状态。

这里需要提及S4,它可以认为是SSM的升级版本。其主要贡献不是HiPPO的魔幻矩阵,而是在拥有HiPPO矩阵的前提下,进行高效的计算。HiPPO是在《HiPPO: Recurrent Memory with Optimal Polynomial Projections. NeurIPS 2020》中定义的。
S4究竟依靠着魔法矩阵A来记住序列的所有历史,因此擅长对长序列建模,核心技术就是在线函数逼近。
-
将输入序列视为时间的连续函数
-
用一组预定义的简单函数的线性组合来近似模拟出输入函数
-
只存储(线性组合的)系数作为状态
-
系数可以通过求解线性常微分方程而(ODE)获得,其中方程参数就是魔幻矩阵A(全场MVP)
-
值得一提的是当将连续时间转换为离散时间,线性ODE就成为了RNN,函数逼近的系数成为该RNN的隐藏状态
-
重建信号也是十分简单,使用给定的隐藏状态(系数)来线性组合多项式基,从而重建所有输入的近似值
HiPPO的论文就是一本行走的数学书,鉴于大部分读者的数学基础,本文不展开具体的推导。中间摘取部分内容主要还是围绕着:在选定度量(或者衰减模式)和基函数的前提下,系数是如何求解出来的,以及魔幻矩阵A是从哪来的。本章温馨提醒:意会即可,不可深究,否则夜不成寐。

HiPPO
HiPPO起源于函数逼近,就是用一系列更简单的函数来逼近一个复杂的函数。相信读者都知道的就是傅里叶变换,它用简单的不同频率的正弦曲线的线性组合来逼近复杂函数。
在原始的HiPPO论文中,研究人员用了多项式作为基函数。函数逼近理论基于泛函分析(一门学科)。 怎么理解呢,可以将它看成是定义在函数空间(而不是向量空间)上的线性代数(高端)版本。
下面的例子可以带给读者一些直观的印象,例如存在三个基向量,每个基向量乘上各自的系数a1,a2,a3进行线性组合就可以得到新的向量。同样的道理可以将A1,A2,A3替换成一组函数。

在泛函分析中将函数f(t)视为无穷维度的向量,也是可以表示为基函数的线性组合。注意这里ei是函数。在实践中当然不可能使用无穷多的基函数,因此一般的做法就是采用有限数量的N个基函数近视模拟。按照常识N越大,近似误差就越小。

S4中使用缩放勒让德多项式(Scaled Legendre Measure),后面会提及的多种优点。下图就采用8个基函数配合不同的系数,拟合出红色的曲线。


魔幻矩阵A
在真实的场景中输入信号是持续进来的,因此模拟和逼近也是时刻进行。

其中f<t定义为目标函数f在时间t之前的逼近和拟合。在时间t1时刻只能观察函数f(黑线)到t1,可以得到如下的组合。
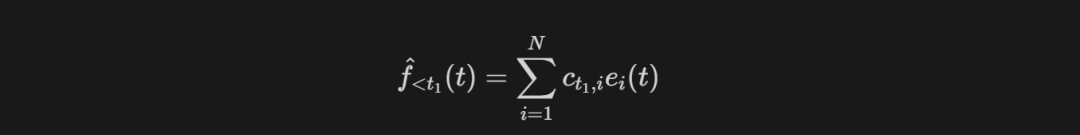
同理当时间窗口来到t4的时候,又得到新的组合。在不同的时间,系统存储的是系数向量,也就是C

那么现在的问题就来到了如何计算系数。解决的办法和线性代数类似,采用计算内积的方式将目标函数f投影到基函数ei。看到这儿不用慌,在泛函分析中,函数和函数之间基于μ的内积的定义公式如下:

μ可以先忽略,这个积分可以看成中学学过的普通积分。对所有系数ci按照上面的公式进行微分并经过(大量)的数学推理将得到一个ODE(微分方程)。在HiPPO的原文中就是这样的,

然后将这个式子整理整理,用向量化来表示就得到公式29。
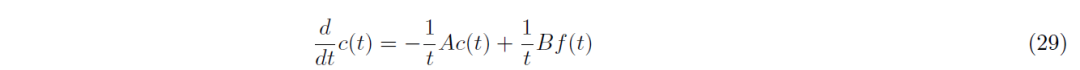
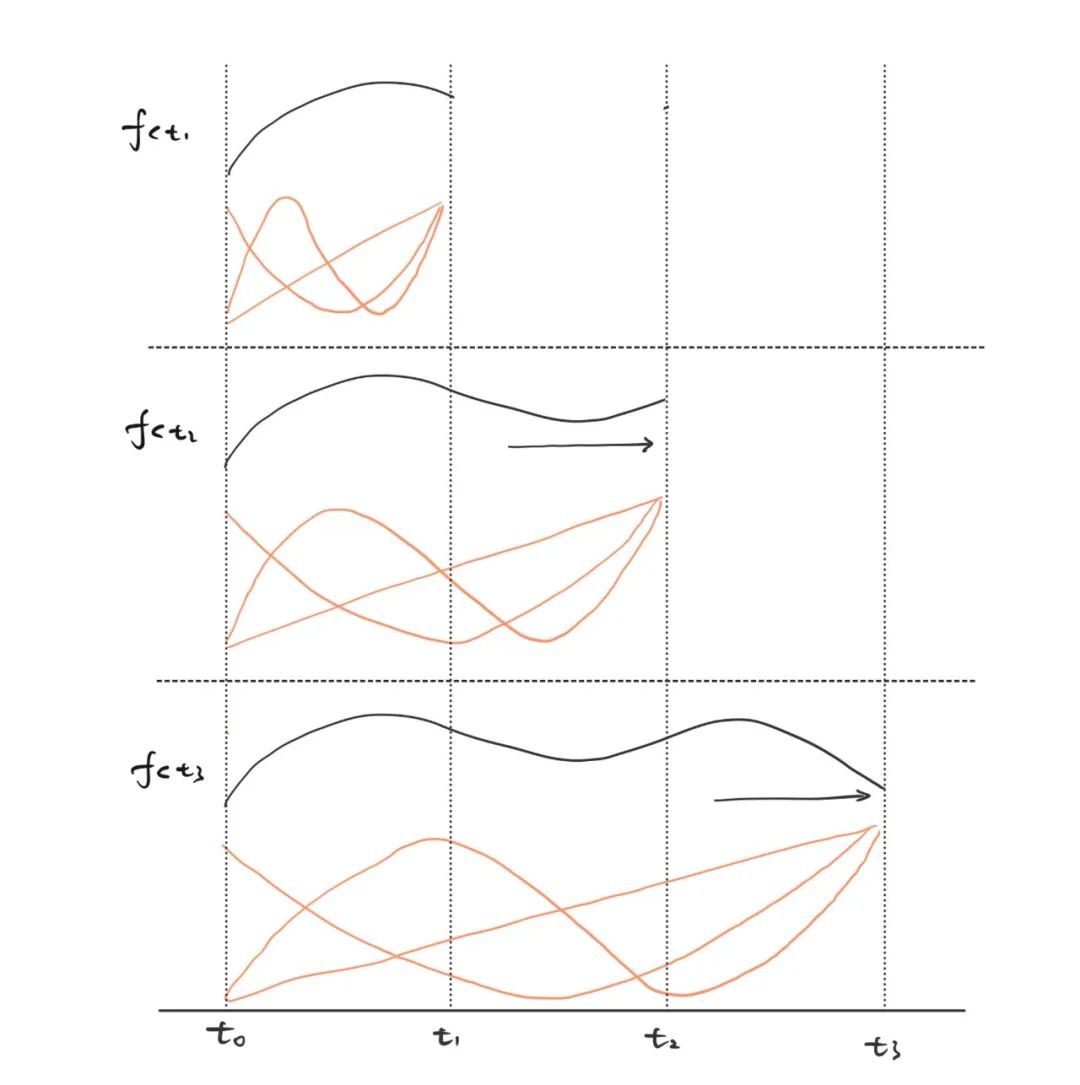
紧接着再仔细观察下公式29,再结合下面连续SSM的公式,是不是很相似。上面的c(t)和下面x(t)一个含义,f(t)和u(t)一个含义。
|
|
|
那么魔幻矩阵A就是这么被推导出来。
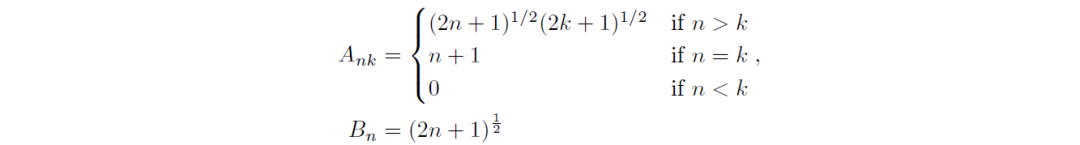

HiPPO框架
刚才提到了度量μ,抛开繁杂的数学公式,可以来这么理解:当用一组函数的线性组合去拟合输入信号的时候,需要有个评估的标准。也就是怎么证明是最优的,或者能够按照期望的模式去拟合。(比如指数衰减还是平均衰减),不同的度量会对应着不同的魔幻矩阵A。因此这里就郑重的提出了HiPPO框架,一般工作流程如下:
-
定义一个度量μ(t)(例如缩放的勒让德度量)或者权重函数ω(t,x)。
-
确定基函数集Pn(t,x)

-
对度量或者权重函数,以及基函数集求导


-
按照02小节进行基于内积与ODE的魔幻矩阵A推导
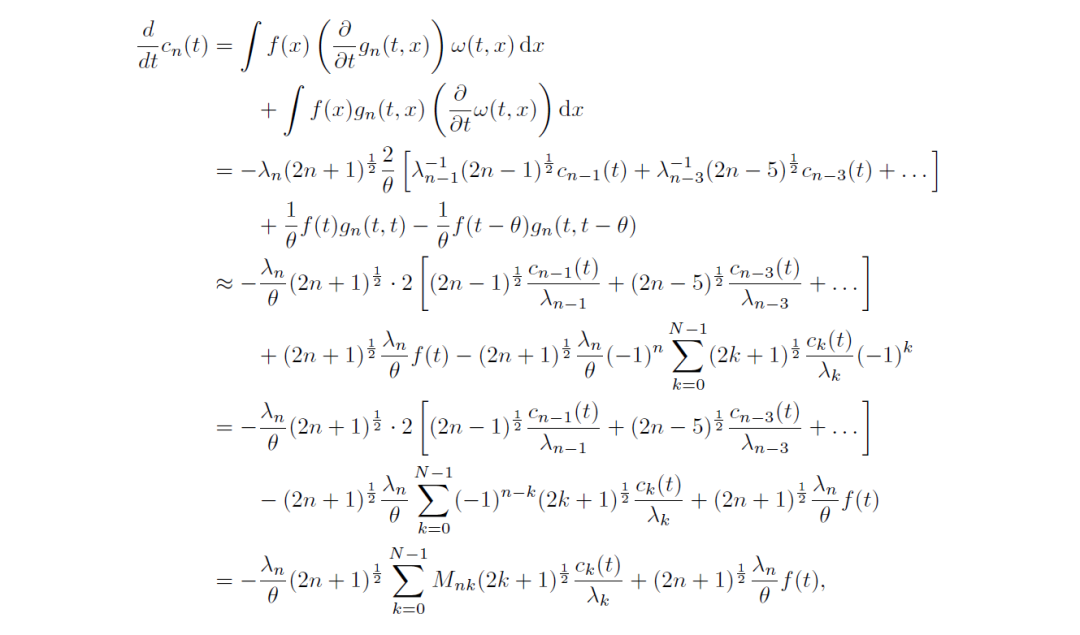
进而得到结果:


动态扩展的勒让德多项式
另外其实随着时间的流动会存在输入信号大于基函数,在HiPPO的论文中研究人员做了一些改进,提出了可以缩放的基多项式。
|
|
|
本文讨论了S4和魔幻矩阵A背后的一些数学原理,核心技术就是在线函数逼近。魔幻矩阵A是为了求解ODE而推导出来,通过求解ODE可以得到这一时刻的线性组合的系数。将连续ODE离散化为离散序列,可以得到RNN。通过改良的RNN能够记住过往的历史,然而计算效率不高。下文将开展S4剩余的部分进行讲解。