Python 求高斯误差函数 erf 和 erfc

news2024/11/27 16:24:33

文章目录

Part.I Introduction
Part.II 概念定义
- Chap.I 误差函数 erf
- Chap.II 误差函数补 erfc
Part.II 求值与绘图
- Chap.I 求取方式
- Chap.II 绘图
Reference

Part.I Introduction

本文将对误差函数（ERror Function, ERF）进行简单的介绍，并探索如何用 Python 来求误差函数。

在这里插入图片描述

更多与之相关的理论知识可以参看关于高斯函数 / 高斯分布 / 高斯误差函数的探讨

Part.II 概念定义

Chap.I 误差函数 erf

误差函数（ERror Function, ERF）的定义式如下
$\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x} e^{-t^2}dt$

Chap.II 误差函数补 erfc

有的地方叫做『误差补函数』或『互补误差函数』，这里我随意取成了误差函数补（ERror Function Complement, ERFC）。一是参考了『舒尔补』这一名字，二是和字母顺序保持一致。

误差函数补（ERror Function Complement, ERFC）的定义式如下

$\operatorname{erfc}(x)=1-\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{x}^{\infty} e^{-t^2}dt$

PS： $\frac{2}{\sqrt{\pi}}\int_{0}^{\infty} e^{-t^2}dt=1$

Part.II 求值与绘图

Chap.I 求取方式

其实很简单

import math

math.erf(x)
math.erfc(x)

比如

>>> import math
>>> math.erf(1)
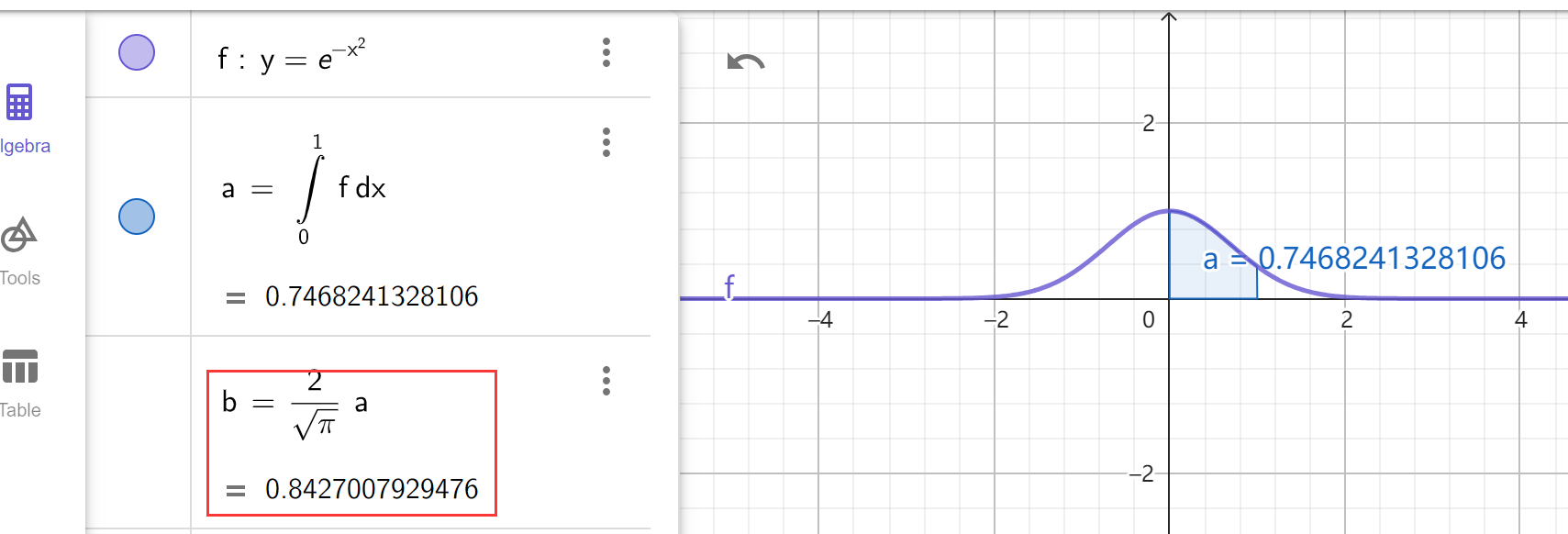
0.8427007929497149
>>> math.erfc(1)
0.1572992070502851
>>> 1-math.erf(1)
0.1572992070502851

GeoGebra 验证如下：

在这里插入图片描述

Chap.II 绘图

使用下面的代码可以绘制处误差函数和误差函数补的图像

import math
import matplotlib.pyplot as plt

def plot_erf():
    x=list(range(0,200))
    x=[i*0.02 for i in x]
    y1=[math.erf(i) for i in x]
    y2=[math.erfc(i) for i in x]
    plt.plot(x,y1)
    plt.plot(x,y2)
    plt.legend(["erf","erfc"])
    plt.show()

plot_erf()