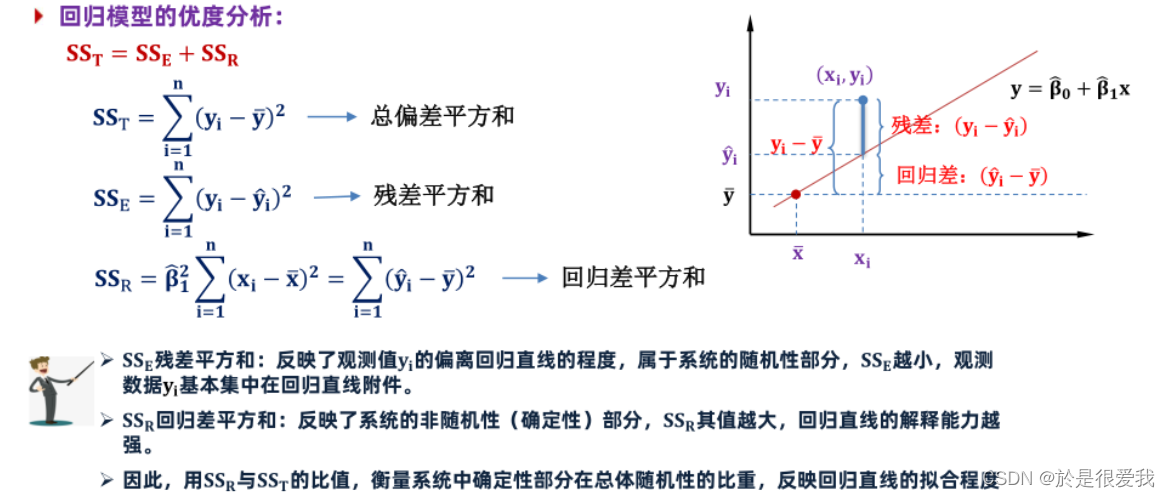
一文让你彻底搞懂最小二乘法（超详细推导）

在进行一元线性回归分析时，使用最小二乘法进行解题，关于最小二乘法具体看上述文章。

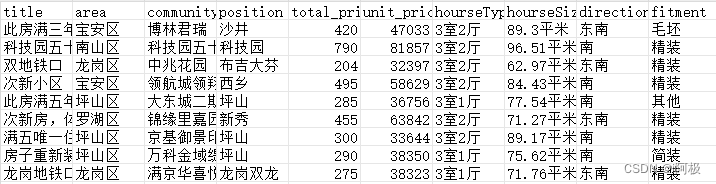
数据文件在文章顶部可见，将第一列数据作为自变量x，第二列数据作为应变量y。建立y与x的关系为线性关系，即y=beta0 + beta1*x。求出：beta0、beta1、回归方程的拟合优度、回归方程的残差平方和。

clc;clear;
% 读取文件中的信息
data = xlsread('OriginalData.xls');

% 提取x和y数据
x = data(:,1);
y = data(:,2);

plot(x,y,'k.','MarkerSize',15);
title('原始数据散点图');
xlabel('x');
ylabel('y');

% 采用最小二乘法
Lxx = sum((x-mean(x)).^2) % 方差
Lxy = sum((x-mean(x)).*(y-mean(y))) % 协方差
beta1 = Lxy/Lxx %斜率
beta0 = mean(y)-beta1*mean(x) %截距

% 计算拟合直线
yhat = @(t) beta0 + beta1 * t;
hold on
plot(x,yhat(x),'LineWidth',2)

% 计算残差平方和
residuals = y - yhat(x); % 计算残差
SS_res = sum(residuals.^2); % 计算残差平方和

% 计算总平方和
SS_tot = sum((y - mean(y)).^2);

% 计算决定系数/拟合优度
R_squared = 1 - SS_res / SS_tot;

fprintf('拟合优度（决定系数）: %.4f\n', R_squared);
fprintf('残差平方和: %.4f\n', SS_res);