快排的简介
快速排序(Quick Sort)是一种高效的排序算法,采用分治法的策略,其基本思想是选择一个基准元素,通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
快速排序的基本步骤:
- 选择基准:从数组中挑选一个元素作为“基准”(pivot)。
- 分区操作(Partitioning):
- 将所有小于基准的元素放置在基准之前,所有大于基准的元素放置在基准之后。这个操作结束后,基准元素就处于数组的中间位置,此位置称为“分割点”。
- 分区操作完成后,基准元素就位于其最终排序后的位置。
- 递归排序:
- 对基准元素左边的子数组递归执行快速排序。
- 对基准元素右边的子数组递归执行快速排序。
快速排序的特点:
- 时间复杂度:
- 最好情况(每次划分都很均匀):O(n log n)。
- 平均情况:O(n log n)。
- 最坏情况(每次划分都将数组分成一个元素与剩余所有元素两部分,例如已排序或逆序数组):O(n^2)。但通过随机选取基准或使用三数取中法等技巧可大幅降低这种情况发生的概率。
- 空间复杂度:
- O(log n),主要来自于递归调用栈的深度。
- 稳定性:
- 快速排序不是稳定的排序算法,因为在交换过程中相等的元素可能会改变原有的相对顺序。
快排的Java代码实现如下所示:
/* 元素交换 */
void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
/* 哨兵划分 */
int partition(int[] nums, int left, int right) {
// 以 nums[left] 为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
swap(nums, i, j); // 交换这两个元素
}
swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}
/* 快速排序 */
void quickSort(int[] nums, int left, int right) {
// 子数组长度为 1 时终止递归
if (left >= right)
return;
// 哨兵划分
int pivot = partition(nums, left, right);
// 递归左子数组、右子数组
quickSort(nums, left, pivot - 1);
quickSort(nums, pivot + 1, right);
}快排流程图如下所示:
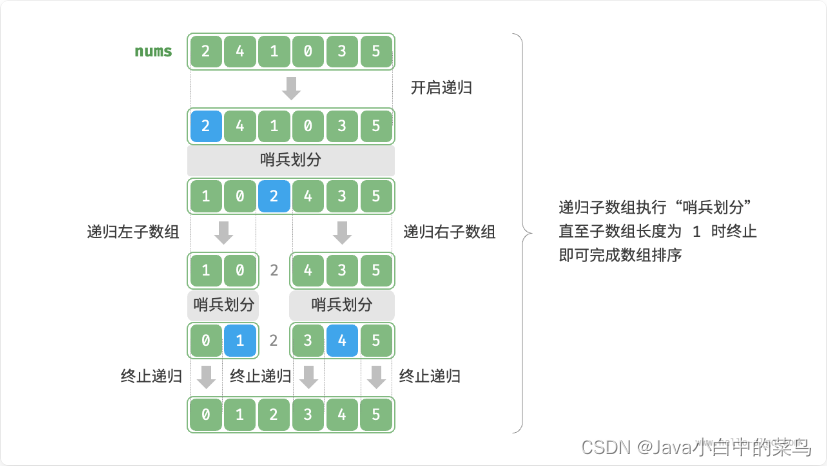
快排优化1:基数优化
快速排序在某些输入下的时间效率可能降低。举一个极端例子,假设输入数组是完全倒序的,由于我们选择最左端元素作为基准数,那么在哨兵划分完成后,基准数被交换至数组最右端,导致左子数组长度为 𝑛−1、右子数组长度为 0 。我们可以在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选元素的中位数作为基准数。这样一来,基准数“既不太小也不太大”的概率将大幅提升。
Java示例代码如下:
/* 选取三个候选元素的中位数 */
int medianThree(int[] nums, int left, int mid, int right) {
int l = nums[left], m = nums[mid], r = nums[right];
if ((l <= m && m <= r) || (r <= m && m <= l))
return mid; // m 在 l 和 r 之间
if ((m <= l && l <= r) || (r <= l && l <= m))
return left; // l 在 m 和 r 之间
return right;
}
/* 哨兵划分(三数取中值) */
int partition(int[] nums, int left, int right) {
// 选取三个候选元素的中位数
int med = medianThree(nums, left, (left + right) / 2, right);
// 将中位数交换至数组最左端
swap(nums, left, med);
// 以 nums[left] 为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
swap(nums, i, j); // 交换这两个元素
}
swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}快排优化2:尾递归优化
尾递归优化是编程中一种优化技术,旨在减少递归调用的开销,尤其是当递归调用是函数体中的最后一个操作时。在快速排序算法中,通常有两个递归调用,分别处理基准元素左侧和右侧的子数组。尾递归优化尝试减少这种递归调用的栈消耗,但需要注意的是,Java等许多现代编程语言默认并不自动执行尾递归优化。尽管如此,我们可以通过手动调整快速排序的递归结构来模拟尾递归的效果,减少递归深度。
在某些输入下,快速排序可能占用空间较多。以完全有序的输入数组为例,设递归中的子数组长度为 𝑚 ,每轮哨兵划分操作都将产生长度为 0 的左子数组和长度为 𝑚−1 的右子数组,这意味着每一层递归调用减少的问题规模非常小(只减少一个元素),递归树的高度会达到 𝑛−1 ,此时需要占用 𝑂(𝑛) 大小的栈帧空间。
为了防止栈帧空间的累积,我们可以在每轮哨兵排序完成后,比较两个子数组的长度,仅对较短的子数组进行递归。由于较短子数组的长度不会超过 𝑛/2 ,因此这种方法能确保递归深度不超过 log𝑛 ,从而将最差空间复杂度优化至 𝑂(log𝑛) 。
为了优化,我们可以使用循环而不是直接递归来控制递归过程,这样做的目的是尽量复用当前函数栈帧,避免每次递归调用都生成新的栈帧。代码如下所示:
/* 快速排序(尾递归优化) */
void quickSort(int[] nums, int left, int right) {
// 子数组长度为 1 时终止
while (left < right) {
// 哨兵划分操作
int pivot = partition(nums, left, right);
// 对两个子数组中较短的那个执行快速排序
if (pivot - left < right - pivot) {
quickSort(nums, left, pivot - 1); // 递归排序左子数组
left = pivot + 1; // 剩余未排序区间为 [pivot + 1, right]
} else {
quickSort(nums, pivot + 1, right); // 递归排序右子数组
right = pivot - 1; // 剩余未排序区间为 [left, pivot - 1]
}
}
}对两个子数组中较短的那个执行快速排序,可以这样理解其好处:
- 减少递归深度:因为处理完较短的子数组后,再次进入递归时,处理的子数组规模相对减小,有助于控制递归调用的总深度。
- 平衡负载:在某些情况下,比如数组已经部分排序,若总是先处理较短的子数组,可以在一定程度上避免递归树严重倾斜,使得递归调用更均匀地分布在左右两侧,从而更高效地利用递归栈空间。
这个策略是一种平衡快速排序递归深度的方法,尤其是在处理大数据集或递归深度受限的环境下尤为重要。通过这样的策略,可以提高算法在极端情况下的健壮性,减少潜在的栈溢出风险。