SPSS中主成分分析功能在【分析】--【降维】--【因子分析】中完成(在SPSS软件中,主成分分析与因子分析均在【因子分析】模块中完成)。
求解主成分通常从分析原始变量的协方差矩阵或相关矩阵着手。
(1)当变量取值的度量单位相同时,选择从协方差矩阵求解;
(2)当变量取值的度量单位不同时,为了消除不同量纲带来的不利影响,应先对数据进行标准化处理,即选择从相关矩阵求解(SPSS默认)。
数据标准化。数据标准化通过【分析】--【描述统计】--【描述】中,勾选“将标准化得分另存为变量”来实现,SPSS会自动将标准化后的数据存入数据表。
相关性检验。进行主成分分析的前提是变量之间存在较高程度的相关性,即信息冗余。可通过相关系数矩阵(大部分>0.3),KMO值(KMO值至少≥0.5,),Bartlett球形度检验(p<α)来完成变量相关性的检验。在SPSS中通过在【分析】--【降维】--【因子分析】--【描述】对话框中勾选相应选项来完成。
- 主成分的选取。原则:
- (1)方差累积贡献率达到80%或85%及以上;
- (2)选取特征值
对应的主成分;
- (3)碎石图。
主成分系数。SPSS输出结果中可以直接得到的是因子载荷矩阵,注意因子载荷矩阵不是主成分系数矩阵
。
,即将因子载荷矩阵第i列的元素除以
,可得对应的主成分系数表,该表中的第i列的元素即为主成分方程中第i个主成分
的系数。
主成分得分。求出主成分系数后,将原始变量Xi的标准化数值代入主成分方程,即可计算主成分得分(SPSS不会直接输出结果)。特别当主成分个数为2时,可在二维平面中绘制散点图(SPSS中通过【图形】--【旧对话框】--【散点/点状】实现),继而分析各样品的分布情况。
开始实战!
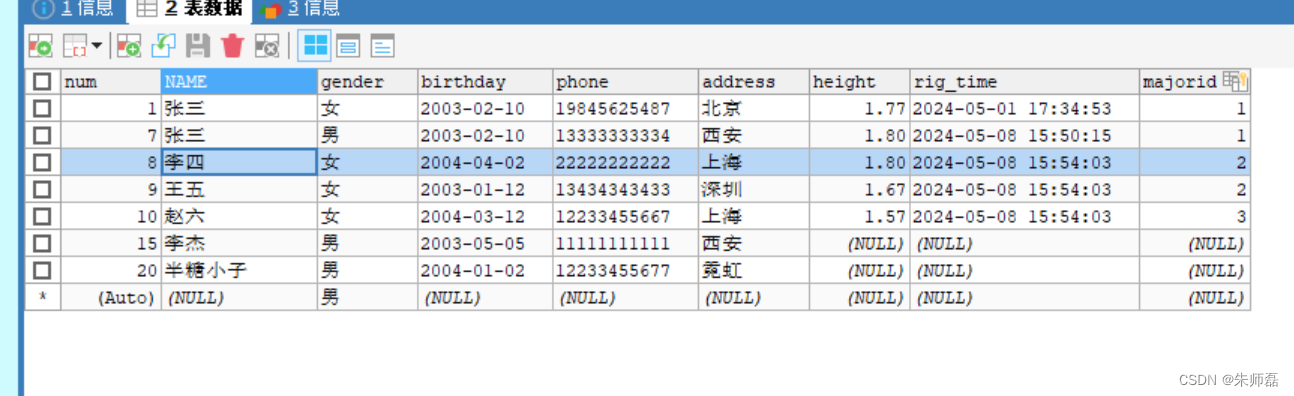
文件:大学生价值观.sav,给出了20名大学生关于价值观的6项测验结果,即样品数n=20,变量数p=6。应用主成分分析方法,分析对大学生价值观起主要作用的变量。
第一步先将数据标准化:[Analyze]→[Descriptive Statistics]→[Descriptives],将六个变量全部添加到“Variable”中,并勾选上“Save standardized values as variables”。
原数据与标准化后的数据对比:

- 主成分分析步骤:[Analyze]→[Dimension Reduction]→[Factor Analysis],将标准化后的六个变量全部添加到“Variables”中;
- 在【Descriptives】对话框中选中“Univariate descriptives”、“Initial solution”和“Coefficients”、“Significance levels”、“Inverse”、“KMO and Bartlett’s test of sphericity”;
- 在【Extraction】对话框中选择“Principal components”方法,输出选择“Unrotated factor solution”和“Scree plot”;
- 在【Rotation】对话框中选择“Varimax”方法,输出选择“Rotated solution”和“Loading plot”。
- 在【Factor Scores】对话框中勾选“Save as variables”保存为变量,并选择“Bartlett”方法,同时勾选“Display factor score coefficient matrix”输出因子得分系数矩阵。
主成分分析结果分析:
相关系数矩阵:将相关系数与0.3作比较,
得出结论:对发展机会的看法和对社会地位的看法的相关系数最高,为0.879;对发展机会的看法和对职位升迁的态度,相关系数为0.826;工作投入程度和对社会地位的看法呈负相关,相关系数为-0.853。
从sig矩阵可知适合做主成分分析。

KMO与Bartlett检验:KMO值与0.5作比较,KMO值为0.637>0.5;Bartlett球形度检验的统计量值,检验p值<0.05,sig<a,适合做主成分分析。

主成分分析的初始解:

特征值与方差贡献度:因为前 2 个主成分的累积方差贡献率达到了 84.115% ,且对应的分别是3.436、1.611,所有
>1,所以选取前 2个主成分。

碎石图:第 3 个特征值以后,变化的趋势开始趋于平稳,所以,取前 2 个主成分是合适的。

因子载荷矩阵:对发展机会的看法、对社会地位的看法、对职位升迁的态度、领导风格的偏好在第1个因子上有较高载荷,所以第1个因子可看成是这几个变量的综合变量。

主成分系数矩阵:

主成分方程:
主成分得分:

主成分二维简单散点图(若提取2个主成分):插入X轴和Y轴,标记样品号。落入第一、四象限的样品相对比较好,落入第二、三象限的样品相对比较差。
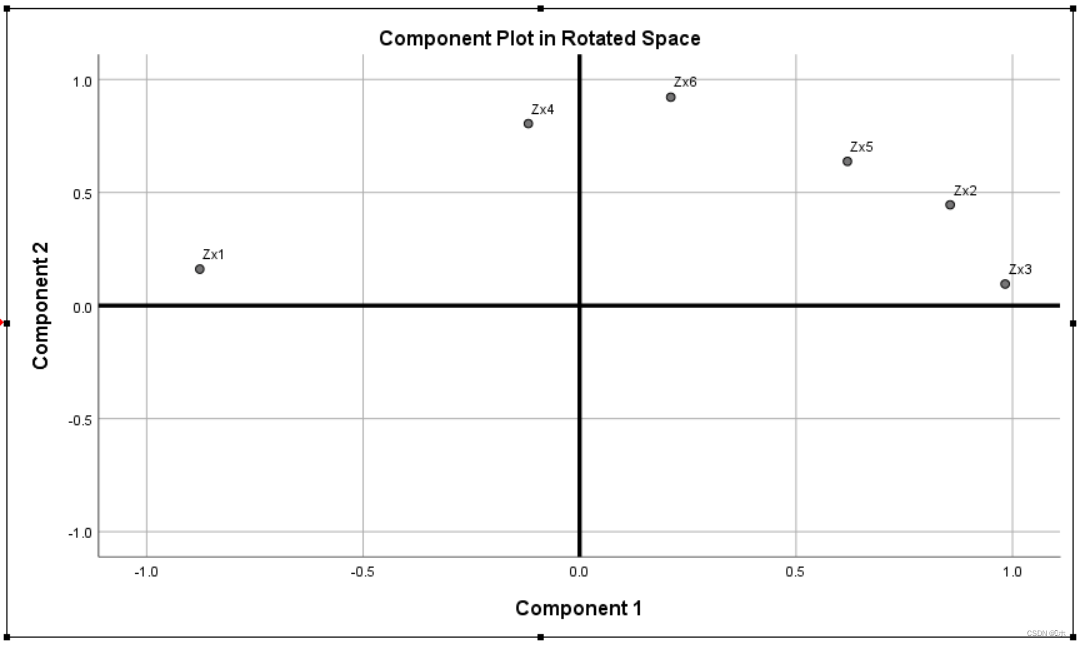
- 结论:
- 样品号1,4落入第一象限;无样品号落入第四象限,这两个象限内第一主成分所占比重最大,所以1,4较好。
- 样品号2,3,5,6落入第二象限,无样品号落入第三象限,这两个象限内第二主成分所占比重最大,所以2,3,5,6较差。