本来挺喜欢刷《剑指offer》的.......（第十一天）

news2024/11/27 2:23:58

跟着博主一起刷题
这里使用的是题库：
https://leetcode.cn/problem-list/xb9nqhhg/?page=1

剑指 Offer 66. 构建乘积数组

剑指 Offer 66. 构建乘积数组
这道题不可使用除法，我们可采用记录前缀积和后缀积的方法，利用两个数组，遍历a数组记录i下标的前缀积和后缀积，最终结果二者相乘即可。

class Solution {
    public int[] constructArr(int[] a) {
        int len=a.length;
        //前缀积和后缀积
        int[] prefix=new int[len];
        int[] suffix=new int[len];
        //初始化
        if(len!=0){
            prefix[0]=1;
            suffix[len-1]=1;
        }
        for(int i=0;i<len-1;i++){
            prefix[i+1]=prefix[i]*a[i];
            suffix[len-1-i-1]=suffix[len-i-1]*a[len-i-1];
        }
        for(int i=0;i<len;i++){
            suffix[i]=suffix[i]*prefix[i];
        }
        return suffix;
    }
}

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
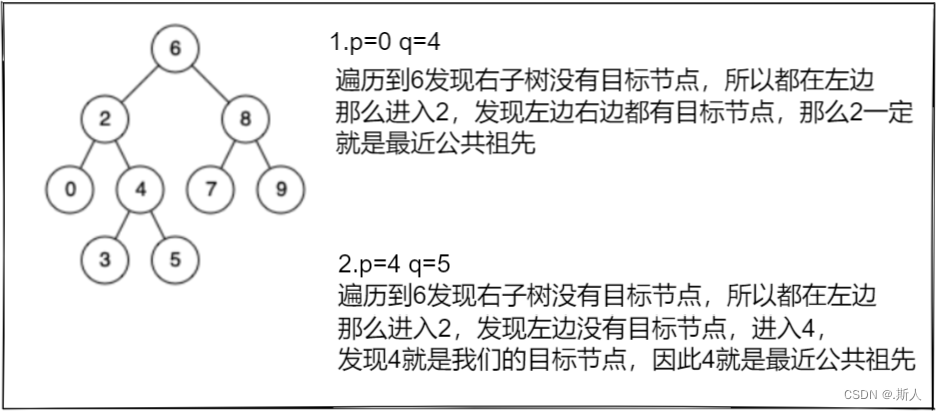
这道题主要在于列举出对于遍历的当前节点所有的可能性来求解：

从这两个例子我们可以提取出全部情况，对于当前节点：
1.1左子树没有目标节点，进入右子树
1.2右子树没有目标节点，进入左子树
2.1左右子树都有目标节点，该节点就是最近公共祖先
3.当前节点=p或q，当前节点为最近公共祖先

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null)return null;
        if(root==p||root==q){
            return root;
        }
        TreeNode left=lowestCommonAncestor(root.left,p,q);;
        TreeNode right=lowestCommonAncestor(root.right,p,q);;
        if(left!=null&&right!=null){
            return root;
        }else if(left==null){
            return right;
        }else{
            return left;
        }
    }
}

由于写完才方法这棵树是搜索树，我们还没有利用二叉搜索树的性质。这样的话就可以利用当前节点值的大小和p，q比较，来判断p和q在哪棵子树上。
1.cur.val>p.val&&cur.val<q.val或cur.val<p.val&&cur.val>q.val
代表cur为最近公共祖先
2.cur.val>p.val&&cur.val>q.val或cur.val<p.val&&cur.val<q.val
大于往右子树走，小于往左子树走
3.cur.valp.val或cur.valq.val
cur为最近公共祖先

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null)return null;
        if(root.val>=p.val&&root.val<=q.val||(root.val<=p.val&&root.val>=q.val)){
            return root;
        }else if(root.val>p.val&&root.val>q.val){
            return lowestCommonAncestor(root.left,p,q);
        }else{
            return lowestCommonAncestor(root.right,p,q);
        }
    }