并查集
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要查找一个元素在哪个集合中。 比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:

现在我们的 Union-Find 算法主要需要实现这两个 API:
class UF {
/* 将 p 和 q 连接 */
public void union(int p, int q);
/* 判断 p 和 q 是否连通 */
public boolean connected(int p, int q);
/* 返回图中有多少个连通分量 */
public int count();
}
比如上面这幅图,0~9 任意两个不同的点都不连通,调用connected都会返回 false,连通分量为 10 个。 如果现在调用union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。 再调用union(1, 2),这时 0,1,2 都被连通,调用connected(0, 2)也会返回 true,连通分量变为 8 个。
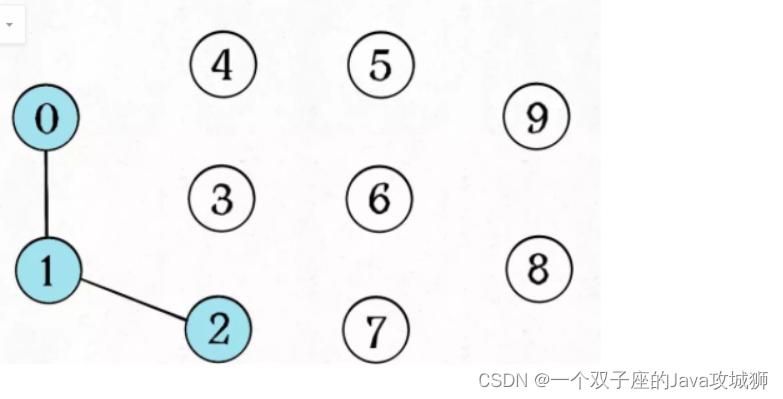
一开始的时候没有相互连通,就是这样:
class UF {
// 记录连通分量
private int count;
// 节点 x 的节点是 parent[x]
private int[] parent;
/* 构造函数,n 为图的节点总数 */
public UF(int n) {
// 一开始互不连通
this.count = n;
// 父节点指针初始指向自己
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
/* 其他函数 */
}
如果要连通两个点,那么则让其中的(任意)一个节点的根节点接到另一个节点的根节点上:
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也一样
count--; // 两个分量合二为一
}
/* 返回某个节点 x 的根节点 */
private int find(int x) {
// 根节点的 parent[x] == x
while (parent[x] != x)
x = parent[x];
return x;
}
/* 返回当前的连通分量个数 */
public int count() {
return count;
}
这样,如果节点p和q连通的话,它们一定拥有相同的根节点:
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
并查集的完整实现:
public class UnionFind {
private int count; //记录连通分量
private int[]parent; //节点x的根节点是parent[x]
public UnionFind(int n){
//一开始互不相通
this.count=n;
//一开始,每个节点是自己的父节点
parent=new int[n];
for (int i = 0; i <n ; i++) {
parent[i]=i;
}
}
/*
将p和q连接, 如果两个节点被连通,那么则让其中的一个根节点连接到另一个节点的根节点上
*/
public void union(int p,int q){
int rootP=find(p);
int rootQ=find(q);
if(rootP==rootQ){
return;
}
//将两颗树合并为一颗
parent[rootP]=rootQ; //parent[rootQ]=rootP 效果是一样的
count--; //两个分量合二为一
}
//返回某个节点x的根节点
private int find(int x){
//根节点的parent[x]==x
while (parent[x]!=x){
x=parent[x];
}
return x;
}
/*
判断p和q是否连通:如果两个节点是连通的,那么他们一定拥有相同的根节点
*/
public boolean connected(int p,int q){
int rootP=find(p);
int rootQ=find(q);
return rootP==rootQ;
}
/*
返回具体有多少个连通分量
*/
public int count(){
return count;
}
}
并查集练习1 冗余连接
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
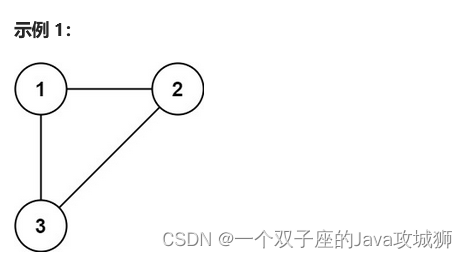
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]
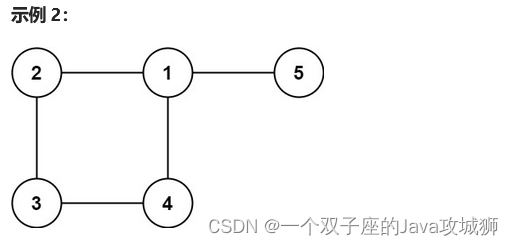
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
解题思路:
树是一个连通且无环的无向图,在树中多了一条附加的边之后就会出现环,因此附加的边即为导致环出现的边。
可以通过并查集寻找附加的边。初始时,每个节点都属于不同的连通分量。遍历每一条边,判断这条边连接的两个顶点是否属于相同的连通分量。
-
如果两个顶点属于不同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间不连通,因此当前的边不会导致环出现,合并这两个顶点的连通分量。
-
如果两个顶点属于相同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间已经连通,因此当前的边导致环出现,为附加的边,将当前的边作为答案返回。
class Solution {
public static int[] findRedundantConnection(int[][] edges) {
int len=edges.length;
UnionFind u=new UnionFind(len+1);
for (int i=0;i<len;i++){
if (u.isConnected(edges[i][0],edges[i][1])){
return new int[]{edges[i][0],edges[i][1]};
}else {
u.union(edges[i][0],edges[i][1]);
}
}
return new int[]{0};
}
}
class UnionFind{
private int count;
private int[] parent;
public UnionFind(int count){
this.count=count;
parent=new int[count];
for (int i=0;i<count;i++){
parent[i]=i;
}
}
public void union(int a,int b){
int parentA=find(a);
int parentB=find(b);
if (parentA==parentB) return;
parent[parentA]=parentB;
count--;
}
public boolean isConnected(int a,int b){
return find(a)==find(b);
}
public int find(int x){
if (x==parent[x]) {
return x;
}else {
parent[x]=find(parent[x]);
return parent[x];
}
}
public int getCount(){
return this.count;
}
}
并查集练习2 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。


解题思路
计算连通分量数的另一个方法是使用并查集。初始时,每个城市都属于不同的连通分量。遍历矩阵 isConnected,如果两个城市之间有相连关系,则它们属于同一个连通分量,对它们进行合并。
遍历矩阵 isConnected 的全部元素之后,计算连通分量的总数,即为省份的总数。
写法一:
class Solution {
public int findCircleNum(int[][] isConnected) {
int len= isConnected.length;
UnionFind u=new UnionFind(len+1);
for (int i=0;i<len;i++){
for (int j=0;j<len;j++){
if (isConnected[i][j]==1) u.union(i+1,j+1);
}
}
return u.getCount()-1;
}
}
class UnionFind{
private int count;
private int[] parent;
public UnionFind(int count){
this.count=count;
parent=new int[count];
for (int i=0;i<count;i++){
parent[i]=i;
}
}
public void union(int a,int b){
int parentA=find(a);
int parentB=find(b);
if (parentA==parentB) return;
parent[parentA]=parentB;
count--;
}
public boolean isConnected(int a,int b){
return find(a)==find(b);
}
public int find(int x){
if (x==parent[x]) {
return x;
}else {
parent[x]=find(parent[x]);
return parent[x];
}
}
public int getCount(){
return this.count;
}
}
写法2
class Solution {
int[] f;
public int findCircleNum(int[][] isConnected) {
int n=isConnected.length;
f=new int[n];
for(int i=0;i<n;i++) {
f[i]=i;
}
for(int i=0;i<isConnected.length;i++) {
for(int j=0;j<isConnected.length;j++) {
if(isConnected[i][j]==1) {
int fi=find(i);
int fj=find(j);
if(fi==fj) {
continue;
}
f[fi]=fj;
}
}
}
int ans=0;
for(int i=0;i<n;i++) {
if(f[i]==i) {
ans++;
}
}
return ans;
}
public int find(int x) {
while(f[x]!=x) {
x=f[x];
}
return x;
}
}
并查集练习3 相似的字符串
如果交换字符串 X 中的两个不同位置的字母,使得它和字符串 Y 相等,那么称 X 和 Y 两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。
例如,“tars” 和 “rats” 是相似的 (交换 0 与 2 的位置); “rats” 和 “arts” 也是相似的,但是 “star” 不与 “tars”,“rats”,或 “arts” 相似。
总之,它们通过相似性形成了两个关联组:{“tars”, “rats”, “arts”} 和 {“star”}。注意,“tars” 和 “arts” 是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。
给定一个字符串列表 strs。列表中的每个字符串都是 strs 中其它所有字符串的一个 字母异位词 。请问 strs 中有多少个相似字符串组?
字母异位词(anagram),一种把某个字符串的字母的位置(顺序)加以改换所形成的新词。
示例 1:
输入:strs = [“tars”,“rats”,“arts”,“star”]
输出:2
示例 2:
输入:strs = [“omv”,“ovm”]
输出:1
解题思路:
我们把每一个字符串看作点,字符串之间是否相似看作边,那么可以发现本题询问的是给定的图中有多少连通分量。于是可以想到使用并查集维护节点间的连通性。
我们枚举给定序列中的任意一对字符串,检查其是否具有相似性,如果相似,那么我们就将这对字符串相连。
在实际代码中,我们可以首先判断当前这对字符串是否已经连通,如果没有连通,我们再检查它们是否具有相似性,可以优化一定的时间复杂度的常数。
class Solution {
int[] f;
public int numSimilarGroups(String[] strs) {
int n=strs.length;
int m=strs[0].length();
f=new int[n];
for (int i = 0; i < n; i++) {
f[i]=i;
}
for (int i=0;i<n-1;i++){
for (int j=i+1;j<n;j++){
int fi=find(i);
int fj=find(j);
if (fi==fj) continue;
if (check(strs[i],strs[j],m)) f[fi]=fj;
}
}
int ans=0;
for (int i = 0; i < n; i++) {
if (f[i]==i) ans++;
}
return ans;
}
public int find(int x){
if (x==f[x]){
return x;
}else {
f[x]=find(f[x]);
return f[x];
}
}
public boolean check(String str1,String str2,int m){
int ans=0;
for (int i = 0; i < str1.length(); i++) {
if (str1.charAt(i)!=str2.charAt(i)){
ans++;
}
if (ans>2){
return false;
}
}
return true;
}
}











![[idekCTF 2023] Malbolge I Gluttony,Typop,Cleithrophobia,Megalophobia](https://img-blog.csdnimg.cn/img_convert/075d78485bd91437286c0636c2fd0896.png)