一、排序的概述

二、插入排序

1、直接插入排序

2、希尔排序

二、选择排序

1、直接选择排序

2、堆排序

三、交换排序

1、冒泡排序

2、快速排序

四、归并排序

五、计数排序

六、基数排序

七、桶排序

八、排序总结

一、排序的概述

排序就是将一组乱序的数据集合变得有序

排序可以分为：

内部排序：数据全部存放在内存中进行排序。

外部排序：数据太多而不能全部存放在内存，整个排序·过程需要在内外存之间多次交换数据才能进行。

根据排序的策略分为：插入排序、选择排序、交换排序和归并排序。

衡量排序的性能指标：

时间复杂度。
空间复杂度。
稳定性：就是排序前后两个相同元素的相对位置保持不变。一个稳定的算法可以变得不稳定，但是一个不稳定的算法不能变得稳定。

排序在我们日常生活中有很多的应用，例如在购物页面可以选择价格从低到高排序，导航时路程可以根据预测花费时间进行排序。

对于排序算法的时间性能测试，采用如下代码：

public static long testTime(int[] array){
        int[] nums = Arrays.copyOf(array, array.length);
        long begin=System.currentTimeMillis();
        sort(nums);//排序算法
        long end=System.currentTimeMillis();
        return end - begin;
    }

二、插入排序

1、直接插入排序

算法思想：就是将待排序的元逐个插入到已将排好序的序列的合适位置，该算法就像扑克牌游戏，每次拿到牌就将牌插入到已排好序的牌的合适位置。

动图演示：

代码实现：

public static void insertSort(int[] array){
        for(int i=1;i<array.length;i++){
            int temp=array[i];
            int j=i-1;
            for(;j>=0;j--){
                if(array[j]>temp){
                    array[j+1]=array[j];
                }else{
                    break;
                }
            }
            array[j+1]=temp;
        }
    }

性能分析：

时间复杂度：O(n^2)。
空间复杂度：O(1)。
稳定性：稳定，因为当待插入的元素小于排好序的序列中的元素时才会进行交换，如果相等就不会进行交换，那么连个相同元素的相对位置保持不变。

2、希尔排序

算法思想：按照下标的一定增量进行的分组，对每组使用直接插入排序，增量逐渐减少，当增量减少为1时，整体再进行一次直接插入排序。

过程演示：

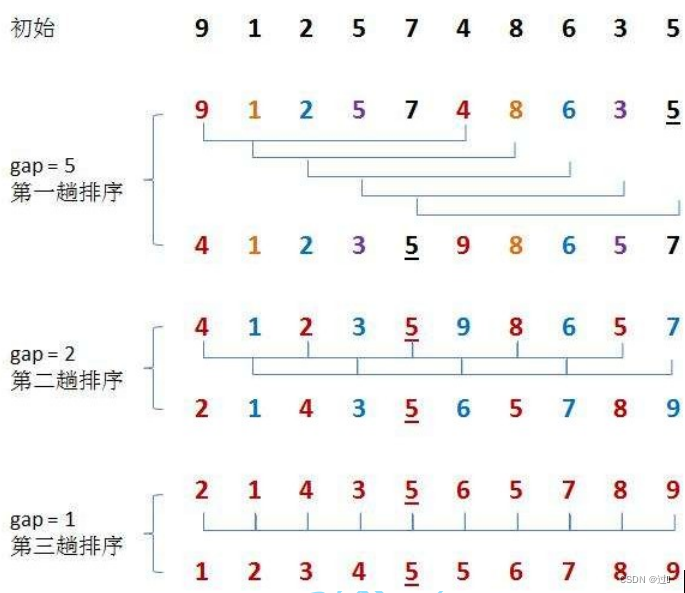
动图演示：

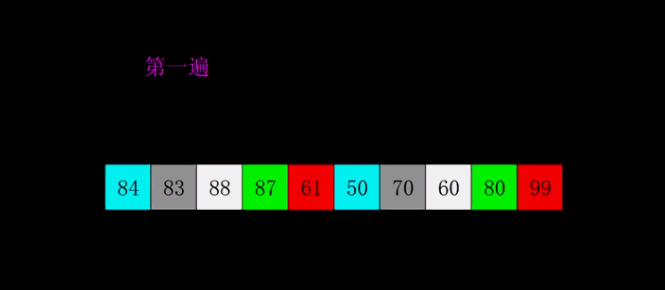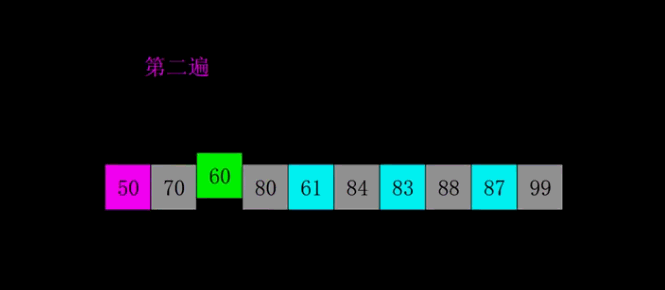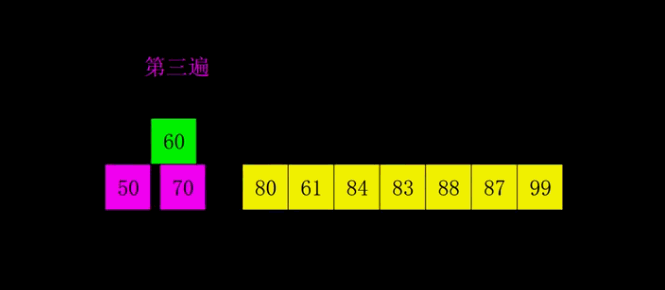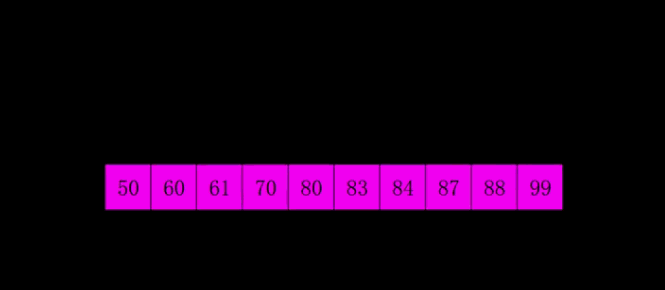
代码实现：

// 希尔排序
public static void shellSort(int[] array){
        int gap=array.length/3+1;
        while(gap>1){
            shell(array,gap);
            gap=gap/3+1;
        }
        shell(array,gap);

    }
private static void shell(int[] array,int gap){
        for(int i=gap;i<array.length;i++){
            int temp=array[i];
            int j=i-gap;
            for(;j>=0;j=j-gap){
                if(array[j]>temp){
                    array[j+gap] = array[j];
                }else{
                    break;
                }
            }
            array[j+gap]=temp;
        }
    }

性能分析：

时间复杂度：O(n^1.3)~O(n^1.5)。
空间复杂度：O(1)
稳定性：不稳定，因为是先分组排序，两个值相等的元素不在一组那么相对顺序就可能发生改变。

二、选择排序

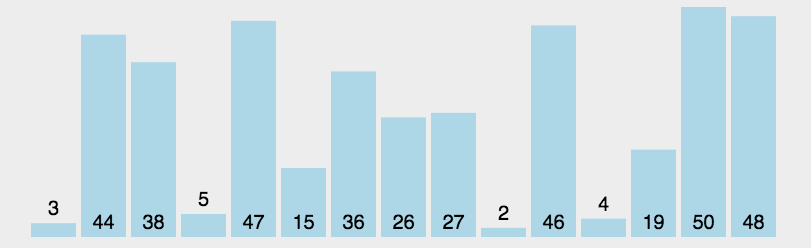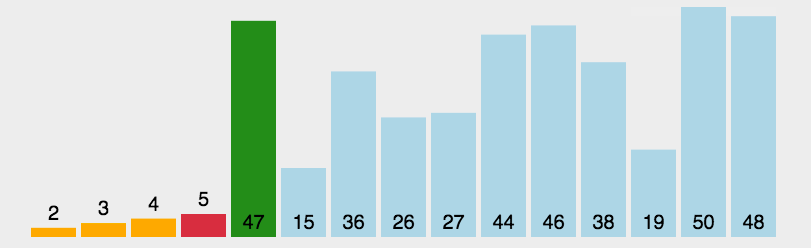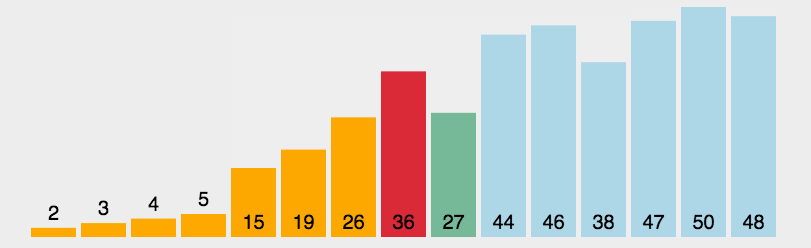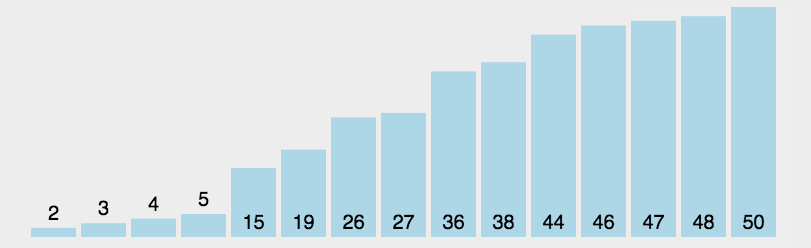
1、直接选择排序

算法思想：每次从待排序的序列中选出一个最小的元素与与序列的起始位置进行交换，直到全部元素排序完成。

动图演示：

代码实现：

public static void selectSort(int[] array){
        for(int i=0;i<array.length;i++){
            int minIndex=i;
            for(int j=i+1;j<array.length;j++){
                if(array[j]<array[minIndex]){
                    minIndex=j;
                }
            }
            int temp=array[i];
            array[i]=array[minIndex];
            array[minIndex]=temp;
        }
    }

性能分析 ：

时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：不稳定，因为选择排序会和序列的起始位置发生交换，就可能导致不稳定。

2、堆排序

算法思想：对数组内部进行排序，不能弹出堆顶元素来进行排序，所以如果要使元素从小到大进行排序就将堆顶元素与最后一个元素交换，每次交换完之后最后一个元素就不再改变，指向下调整堆之后，堆顶与上一个最后元素的前一个元素进行交换，依次类推，直到所有位置的元素都已确定。

动图演示：

代码实现：

// 堆排序
public static void heapSort(int[] array){
        createHeap(array);
        int end=array.length-1;
        for(int i=end;i>0;i--){
            int temp=array[i];
            array[i]=array[0];
            array[0]=temp;
            shiftDown(array,0,end);
            end--;
        }
    }
//创建堆
private static void createHeap(int[] array){
        for(int i=(array.length-1-1)/2;i>=0;i--){
            shiftDown(array,i,array.length);
        }
    }
//向下调整
private static void shiftDown(int[] array,int parent,int len){
        int child=2*parent+1;
        while (child < len){
            if(child+1 < len &&array[child+1] > array[child]){
                child++;
            }
            if(array[child]>array[parent]){
                int temp=array[child];
                array[child]=array[parent];
                array[parent]=temp;
                parent=child;
                child=2*parent+1;
            }else{
                break;
            }
        }
    }

性能分析：

时间复杂度：O(nlog2 n)。
空间复杂度：O（1）。
稳定性：不稳定。

三、交换排序

1、冒泡排序

算法思想：相邻元素两两进行比较，若发生逆序就进行交换，直至待排序的元素序列中没有逆序。

动图演示：

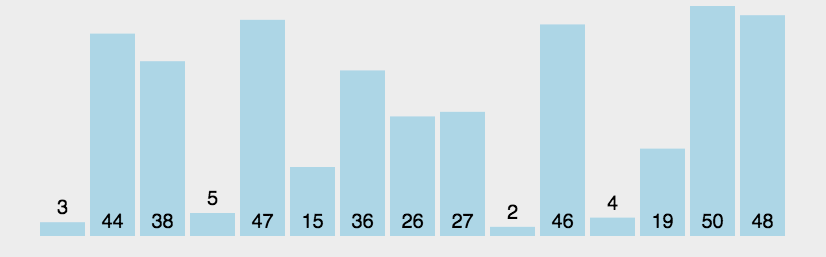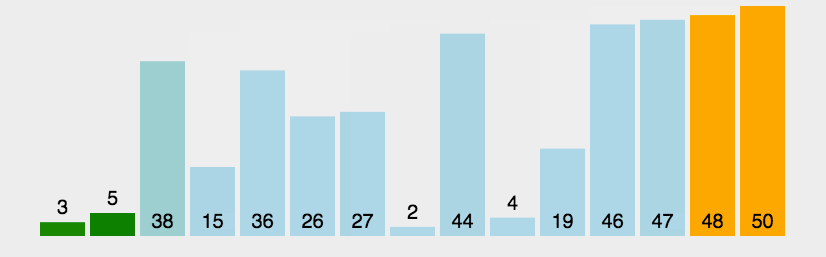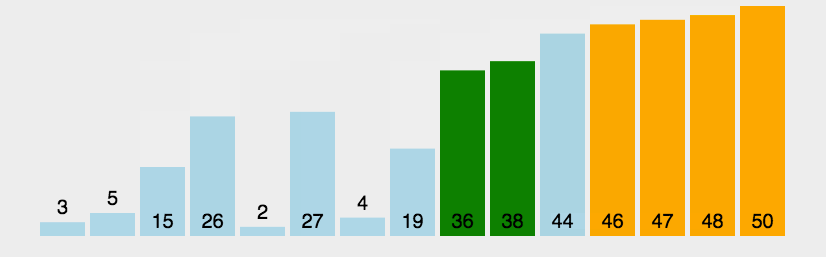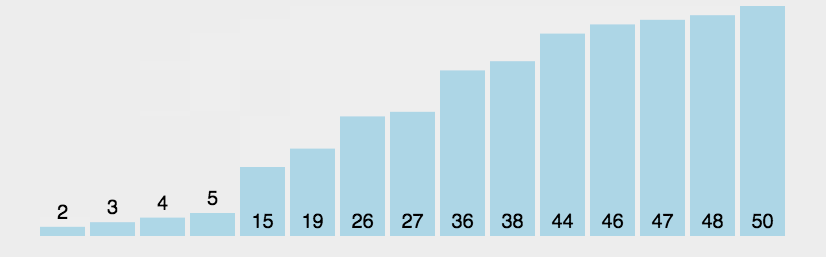
代码实现：

public static void bubbleSort(int[] array){
        for(int i=0;i<array.length;i++){
            boolean flag=true;
            for(int j=0;j<array.length-i-1;j++){
                if(array[j]>array[j+1]){
                    int temp=array[j];
                    array[j]=array[j+1];
                    array[j+1]=temp;
                    flag=false;
                }
            }
            if(flag){
                break;
            }
        }
    }

性能分析：

时间复杂度：O(n^2)。
空间复杂度：O(1)。
稳定性：稳定。

2、快速排序

算法思想：在待排序的序列中选择一个基准，按照基准将元素分成左右两个子序列，使得左边的子序列的元素都小于基准元素，使得右边的子序列都大于基准元素，对左右子序列继续重复上述步骤，使得每个子序列的长度为1为止。

动图演示：

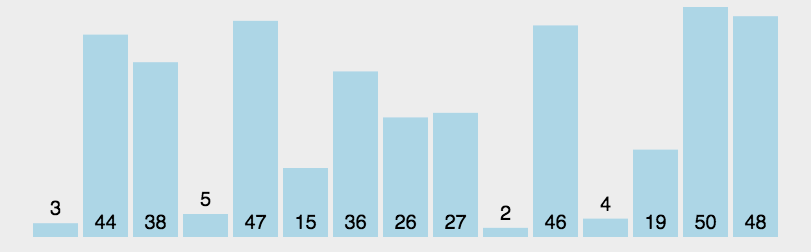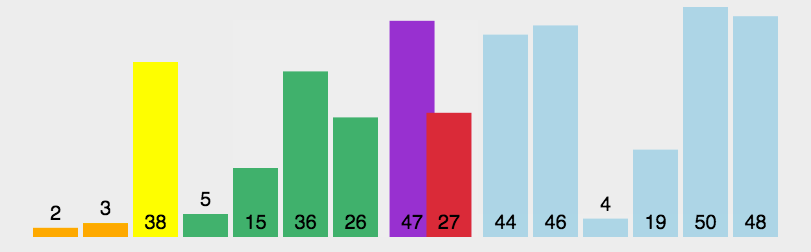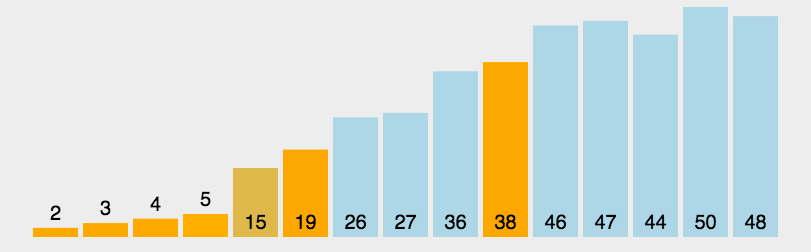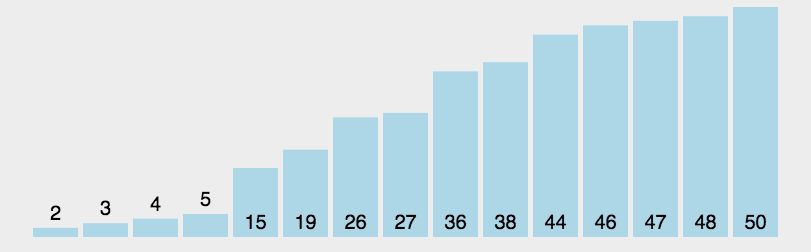
代码实现：

public static void quickSort(int[] array){
        
        quick(array,0,array.length - 1);
    }
    public static void quick(int[] array,int left,int right){
        if(left >= right){
            return;
        }
        int part = partition(array,left,right);
        quick(array,left,part -1);
        quick(array,part + 1,right);
    }
    public static int partition(int[] array,int start,int end){
        int temp=array[start];
        while(start < end){
            while(start < end && array[end] >= temp){
                end--;
            }
            array[start] = array[end];
            while (start < end && array[start] <= temp){
                start++;
            }
            array[end] = array[start];
        }
        array[start] = temp;
        return start;
    }

性能分析：

时间复杂度：O(nlog2 n)。
空间复杂度：O(log2 n)。
稳定性：稳定。

上述快速排序的时间复杂度是在最好情况下的，最坏情况下整个待排序元素是顺序或是逆序的，时间复杂度高达O(n^2),并且当数据量很大的时候，空间复杂度也是很大的，可能会出现栈溢出，所以需要进行优化：

每次选择基准元素时采用三数取中法，就是将right坐标、left坐标的值和mid中间值约束，以确保每次的基准元素不是最大值或最小值，还有当子序列长度不太大时，可以使用直接插入排序来提高效率。

public static void quickSort(int[] array){
        quick(array,0,array.length - 1);
    }
    public static void quick(int[] array,int left,int right){
        if(left >= right){
            return;
        }
        if(right-left <=15){
            insertSort(array,left,right);
            return;
        }
        int index = midThree(array,left,right);
        int temp = array[index];
        array[index] = array[left];
        array[left] = temp;
        int part = partition(array,left,right);
        quick(array,left,part -1);
        quick(array,part + 1,right);
    }
    public static int partition(int[] array,int start,int end){
        int temp=array[start];
        while(start < end){
            while(start < end && array[end] >= temp){
                end--;
            }
            array[start] = array[end];
            while (start < end && array[start] <= temp){
                start++;
            }
            array[end] = array[start];
        }
        array[start] = temp;
        return start;
    }
    public static void insertSort(int[] array,int left,int right){
        for(int i = left+1;i <= right;i++){
            int temp = array[i];
            int j = i-1;
            for(;j >=left;j--){
                if(array[j] > temp){
                    array[j+1] = array[j];
                }else{
                    break;
                }
            }
            array[j+1] = temp;
        }
    }
    public static  int midThree(int[] array,int left,int right){
        int mid=(left+right) / 2;
        if(array[left] < array[right]){
            if(array[mid] > array[left]){
                return mid;
            }else{
                return left;
            }
        }else{
            if(array[mid] > array[right]){
                return mid;
            }else{
                return right;
            }
        }
    }

快速排序也可以非递归实现：利用栈将每次划分的左右子序列的下标入栈，只要栈不为空，每次弹出两个元素，作为调整区间的下标。直到子序列只有一个元素的时候就停止入栈。

代码实现：

public static void quickSort2(int[] array){
        Deque<Integer> stack = new LinkedList<>();
        int left=0;
        int right=array.length-1;
        stack.push(left);
        stack.push(right);
        while (!stack.isEmpty()){
            right=stack.pop();
            left=stack.pop();
            int part=partition(array,left,right);
            if(part > left+1){
                stack.push(left);
                stack.push(part-1);
            }
            if(part < right-1){
                stack.push(part+1);
                stack.push(right);
            }

        }
    }

四、归并排序

算法思想：采用的是分治法的思想，先把待排序的序列分解成若干个子序列，先让子序列有序，然后将有序的子序列合并是整个待排序的序列。

动图演示：

代码实现：

public static void mergeSort(int[] array){
        divideMerge(array,0,array.length-1);
    }
    public static void divideMerge(int[] array,int left,int right){
        if(left >= right){
            return;
        }
        int mid=(left+right) / 2;
        divideMerge(array,left,mid);
        divideMerge(array,mid+1,right);
        merge(array,left,right,mid);
    }
    public static void merge(int[] array,int left,int right,int mid){
        int s1=left;
        int s2=mid+1;
        int[] nums=new int[right-left+1];
        int k=0;
        while(s1 <= mid && s2 <= right){
            if(array[s1]<array[s2]){
                nums[k++] = array[s1++];
            }else{
                nums[k++] = array[s2++];
            }
        }
        while(s1 <= mid){
            nums[k++] = array[s1++];
        }
        while (s2 <= right){
            nums[k++] = array[s2++];
        }
        for(int i=0;i< k;i++){
            array[i+left]=nums[i];
        }
    }

性能分析：

时间复杂度：O(nlog2 n)。
空间复杂度：O(n)。
稳定性：稳定。

同样，归并排序也可以进行非递归实现。

 public static void mergeSort2(int[] array) {
        int gap = 1;
        while (gap < array.length) {
            for (int i = 0; i < array.length; i = i + gap * 2) {
                int left = i;
                int mid = left + gap - 1;
                if (mid >= array.length) {
                    mid = array.length - 1;
                }
                int right = mid + gap;
                if (right >= array.length) {
                    right = array.length - 1;
                }
                merge(array, left, right, mid);
            }
            gap *= 2;
        }
    }

海量数据的排序问题：

外部排序：排序过程需要在磁盘等外部存储进行的排序

前提：内存只有 1G ，需要排序的数据有 100G

解决方案：因为待排序的数据有100G而内存只有1G，那么就可以将待排序的数据等分为200份，每份数据大小为512M，然后将每份数据存入内存中排好序，然后对这200份数据在内存外进行再进行归并排序即可。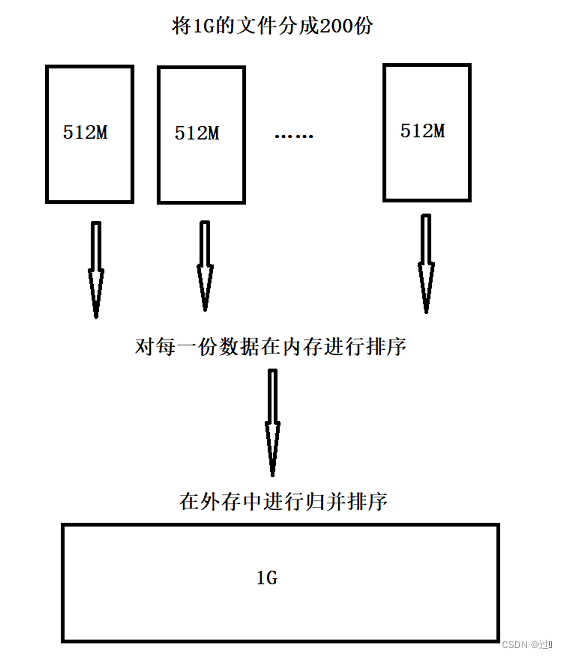

五、计数排序

算法思想：利用鸽巢原理，开辟一段较大的空间的数组，数组中默认元素为0,将待排序的元素对应到下标所对应的元素值加一，计数排序主要应用于待排序的序列在某个范围内。

动图演示：

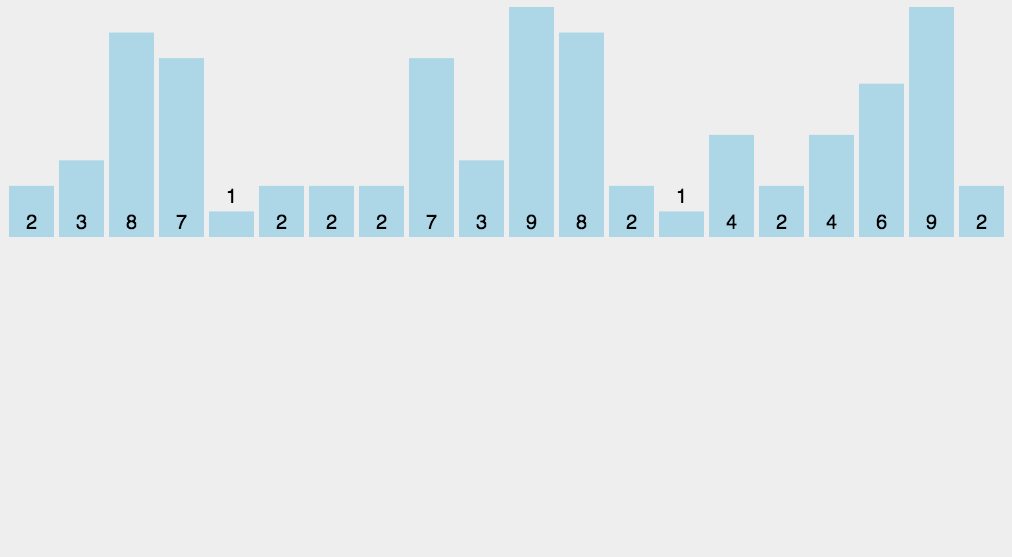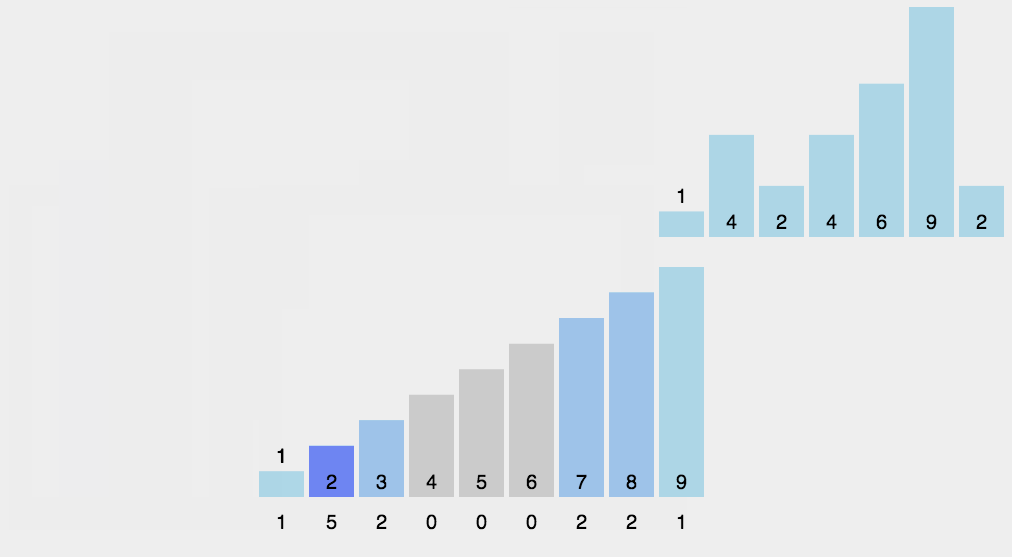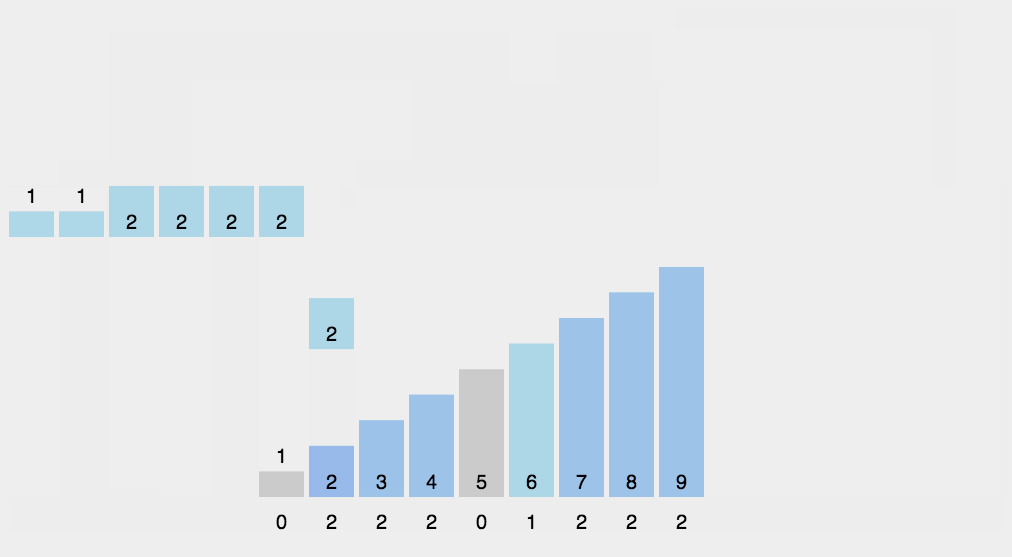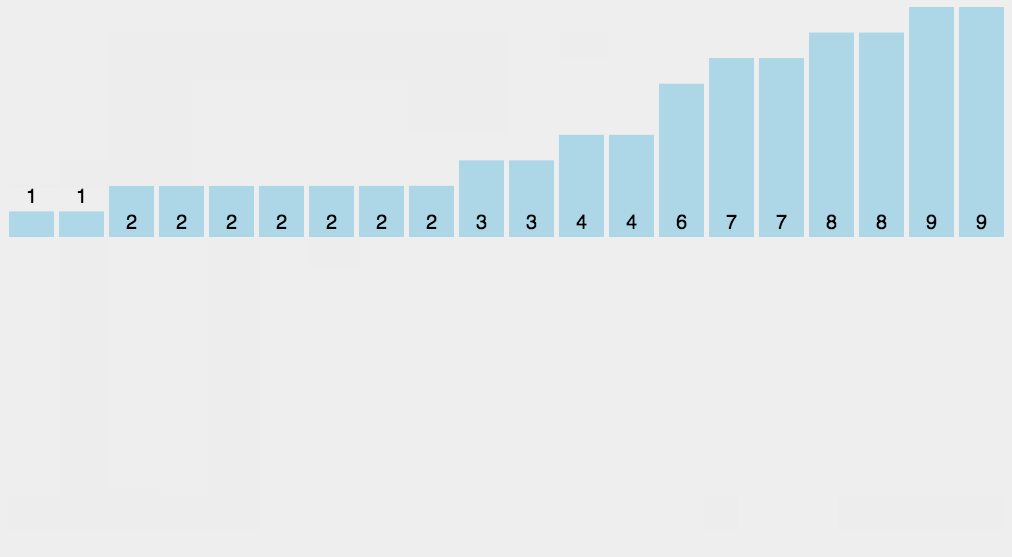
代码实现：

public static void countingSort(int[] array){
        int min = array[0];
        int max = array[0];
        for(int i = 1;i < array.length;i++){
            if(array[i] < min){
                min = array[i];
            }
            if(array[i] > max){
                max = array[i];
            }
        }
        int[] nums = new int[max-min+1];
        for(int i = 0;i < array.length;i++){
            nums[array[i]-min]++;
        }
        int k=0;
        for(int i = 0;i < nums.length;i++){
            while(nums[i] != 0){
                array[k++] = min+i;
                nums[i]--;
            }
        }
    }

性能分析：

时间复杂度：O(max(n,数组范围))。
空间复杂度：O(数组范围)。
稳定性：稳定。

六、基数排序

算法思想：基数排序是对数字的每一位进行排序的，最大数字的位数决定了排列的次数，每次先排列，然后再收集，重复上述步骤，直到最高位排序完成。

动图演示：

代码实现：

 //基数排序
    public static void baseSort(int[] array){
        int max = array[0];
        for(int i = 1;i < array.length;i++){
            if(array[i] > max){
                max = array[i];
            }
        }
        int count=countByte(max);
        LinkedList<LinkedList<Integer>> lists = new LinkedList<>();
        for(int i = 0;i < 10;i++){
            lists.add(new LinkedList<>());
        }
        int k=1;
        while(k <= count){
            for(int i = 0;i < array.length;i++){
                int num = getByteNum(array[i],k);
                lists.get(num).add(array[i]);
            }
            int j = 0;
            for(int i = 0;i < lists.size();i++){
                while(!lists.get(i).isEmpty()){
                    array[j++] =lists.get(i).poll();
                }
            }
            k++;

        }
    }
    //计算出数字的位数
    public static int countByte(int num){
        int count = 0;
        while(num != 0){
            num=num/10;
            count++;
        }
        return count;
    }
    //获取到指定位的数字
    public static int getByteNum(int num,int index){
        String s = String.valueOf(num);
        if(index <= s.length()){
            return (int)(s.charAt(s.length() - index) - '0');
        }
        return 0;

    }

性能分析：

时间复杂度：O(n*k)。
空间复杂度：O(n+k)。
稳定性：稳定。

七、桶排序

算法思想：将待排序的序列划分为多个范围大小相同的区间，将元素分别放入到对应的区间，对每个子区间进行排序，最后整个序列变得有序。

动图演示：

代码实现：

public static void bucketSort(int[] array){
        int min = array[0];
        int max = array[0];
        for(int i = 1;i < array.length;i++){
            if(array[i] < min){
                min = array[i];
            }
            if(array[i] > max){
                max = array[i];
            }
        }
        int size = (max-min) / array.length + 1;
        LinkedList<LinkedList<Integer>> lists = new LinkedList<>();
        for(int i = 0;i < size;i++){
            lists.add(new LinkedList<>());
        }
        for(int i = 0;i < array.length;i++){
            int num = (array[i] - min) / size;
            lists.get(num).add(array[i]);
        }
        int k=0;
        for(int i = 0;i < size;i++){
            lists.get(i).sort(new Comparator<Integer>() {
                @Override
                public int compare(Integer o1, Integer o2) {
                    return o1-o2;
                }
            });
            while(!lists.get(i).isEmpty()){
                array[k++]=lists.get(i).poll();
            }
        }
    }

性能分析：

时间复杂度：O(n+k)。
空间复杂度：O(n+k)。
稳定性：稳定。

八、排序总结

算法名称	时间复杂度	空间复杂度	稳定性
直接插入排序	O(n^2)	O(1)	稳定
希尔排序	O(n^1.3)	O(1)	不稳定
直接选择排序	O(n^2)	O(1)	不稳定
堆排序	O(nlog2 n)	O(1)	不稳定
冒泡排序	O(n^2)	O(1)	稳定
快速排序	O(nlog2 n)	O(log2 n)	不稳定
归并排序	O(nlog2 n)	O(n)	稳定
计数排序	O(nlog2 n)	O(n)	稳定
基数排序	O(n*k）	O(n+k)	不稳定
桶排序	O(n+k)	O(n+k)	稳定