文章目录
- 神经网络模型的构成
- BP神经网络
神经网络模型的构成
三种表示方式:

神经网络的三要素:
- 具有突触或连接,用权重表示神经元的连接强度
- 具有时空整合功能的输入信号累加器
- 激励函数用于限制神经网络的输出
感知神经网络

BP神经网络
BP神经网络的学习由信息的正向传播和误差的反向传播两个过程组成,学习规则采用W-H学习规则(最小均方差,梯度下降法),通过反向传播,不断调整网络的权重和阈值,使得网络的误差平方和最小。
BP神经网络模型通用描述:
z
(
k
)
=
w
(
k
)
x
(
k
)
+
b
(
k
)
y
(
k
)
=
f
(
z
(
k
)
)
z^{(k)} = w^{(k)}x^{(k)} + b^{(k)} \\y^{(k)} = f(z^{(k)})
z(k)=w(k)x(k)+b(k)y(k)=f(z(k))
o ( k ) = f ( w ( k ) o ( k − 1 ) + b ( k ) ) o^{(k)} = f(w^{(k)}o^{(k - 1)} + b^{(k)}) o(k)=f(w(k)o(k−1)+b(k))
损失函数的构建
E
=
1
2
n
∑
p
=
1
n
(
T
p
−
Q
p
)
2
E = \frac{1}{2n} \sum\limits_{p=1}^{n}(T_p - Q_p)^2
E=2n1p=1∑n(Tp−Qp)2
预测的输出值减期望的输出值的均方差
梯度下降法:
W
(
k
+
1
)
=
W
k
−
a
∗
α
α
w
k
∗
E
(
w
k
,
b
k
)
b
(
k
+
1
)
=
b
k
=
a
∗
α
α
b
k
∗
E
(
w
k
,
b
k
)
W_{(k +1)} = W_{k} - a * \frac{\alpha}{\alpha w_k} * E(w_k, b_k) \\ b_{(k + 1)} = b_k = a * \frac{\alpha}{\alpha b_k} * E(w_k, b_k)
W(k+1)=Wk−a∗αwkα∗E(wk,bk)b(k+1)=bk=a∗αbkα∗E(wk,bk)
而:
α
α
w
k
∗
E
=
1
2
m
∗
∑
i
=
1
m
∗
2
∗
(
w
k
x
i
+
b
−
y
i
)
∗
x
i
α
α
b
k
∗
E
=
1
2
m
∗
∑
i
=
1
m
∗
2
∗
(
w
k
x
i
+
b
−
y
i
)
\frac{\alpha}{\alpha w_k} * E = \frac{1}{2m} * \sum\limits_{i = 1}^{m} *2 * (w_k x^i + b - y^i) * x^i \\ \frac{\alpha}{\alpha b_k} * E = \frac{1}{2m} * \sum\limits_{i = 1}^{m} *2 * (w_k x^i + b - y^i)
αwkα∗E=2m1∗i=1∑m∗2∗(wkxi+b−yi)∗xiαbkα∗E=2m1∗i=1∑m∗2∗(wkxi+b−yi)
当采用sigmoid激活函数:
导数:
f
′
(
n
e
t
j
l
)
=
f
(
n
e
t
j
l
)
(
1
−
f
(
n
e
t
j
l
)
)
f'(net^l_j) = f(net^l_j)(1 - f(net^l_j))
f′(netjl)=f(netjl)(1−f(netjl))
(
1
1
+
e
−
z
)
′
=
(
1
1
+
e
−
z
)
∗
(
1
−
1
1
+
e
−
z
)
(\frac{1}{1 + e^{-z}})' = (\frac{1}{1 + e^{-z}}) * (1 - \frac{1}{1 + e^{-z}})
(1+e−z1)′=(1+e−z1)∗(1−1+e−z1)
对于交叉熵损失函数有:

例题:
给定神经网络如下:
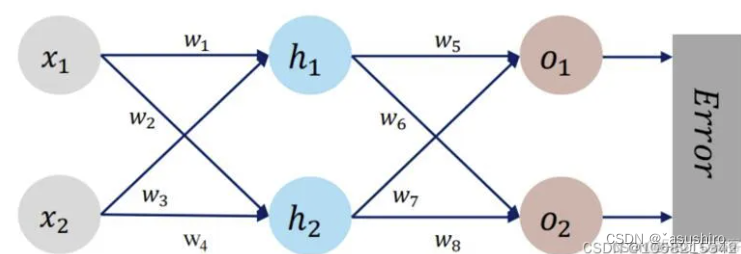
输入值为:x1, x2 = 0.5, 0.3
期望输出值为y1, y2 = 0.23, -0.07
给出正向传播的初始参数为
w
1
w_1
w1~
w
8
w_8
w8为0.2 -0.4 0.5 0.6 0.1 -0.5 -0.3 0.8
采用平方损失函数,梯度下降法求解第一轮更新后的参数。

训练步骤
- 表达:计算训练的输出矢量 A = W ∗ P + B A = W * P + B A=W∗P+B,以及与期望输出之间的误差;
- 检查:将网络输出误差的平方和与期望误差相比较,如果其值小于期望误差,或训练以达到实现设定的最大训练次数,则停止训练;否则继续。
- 学习:采用最小均方差和梯度下降方法计算权值和偏差,并返回到1
BP算法的改进
- 带动量因子算法
- 自适应学习速率
- 改变学习速率的方法
- 作用函数后缩法
- 改变性能指标函数
![[嵌入式系统-75]:RT-Thread-快速上手:正点原子探索者 STM32F407示例](https://img-blog.csdnimg.cn/img_convert/26603420183b22ef3cc660398726387e.gif)