1.EMV决策树
定义:用决策树在若干备选行动方案中选择一个最佳方案。在决策树 中,用不同的分支代表不同的决策或事件,即项目的备选路径。每个决策或事件 都有相关的成本和单个项目风险(包括威胁和机会)。决策树分支的终点表示沿特 定路径发展的最后结果,可以是负面或正面的结果。在决策树分析中,通过计算每条分支的预期货币价值,就可以选出最优的路径。
EMV=盈利百分比影响值-风险百分比影响值
EMV =概率 ,*路径净值 ₁+概率 ₂*路径净值 ₂+概率 ₃+路径净值 .+概率 n*路径净值 n
2.沟通渠道
沟通渠道=n *(n-1)/2 【注:n 代表干系人数量】
3.自制/外购分析
对比成本大小、技术、涉密、长期使用等方面对比
4.计算加权系统
定义:是采购管理中“供方选择”里的工具和技术。加权系统是对定性数据的一种定量分析方法,以减少在渠道中人为偏见带来的影响。通过给项赋予不同的权重,求结果。
n 项分值之和除以 n,乘以权重比例。 得分=(分1 +分2+...+分n)/n * 权重
例如:
5.系统可用性
定义:在要求的外部资源得到保证的前提下,产品你在规定的条件下和规定的时刻或时间区间内处于可执行规定功能状态的能力,它是产品可靠性、维修性和维修保障性的综合反映。
系统可用性=可用时间/总时间
=平均无故障时间/(平均无故障时间+平均维修时间)*100%
例题:
6.投资回收期(Payback Pierod)
1)资金的时间价值:
不同时间发生的等额资金在价值上的差异。资金等值,是指在时间因素的作用下,在不同时期,绝对值不等的资金 具有相等的价值。
如:年利率5%条件下,当年的100元与下一年的 100*(1+5%)=1等值的。
而当年的100元,与上一年的 100/(1+5%)=95.23 等值的。
2)项目的经济价值(可行性分析):
根据是否考虑资金的时间价值,分为动态评价、静态评价。
静态评价:进行项目方案效益和费用的计算时,不考虑自资金的时间价值,不计利息。
动态评价:把不同时点的效益和费用 折算为同一时点的 等值价值。
(1) 净现值 NPV
净现值 NPV:从投资 到产出 每个年份的净收益 转成现值相加。
计算 简化: 根据现值 算终值 F= P(1+R)n次方,相反 就除。
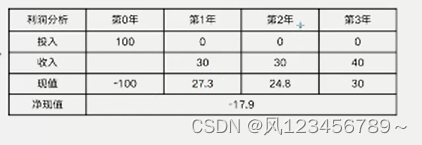
例子1:年利率 10%,投入、收入如下图,计算现值、净现值。
解答:净现值 NPV= -100+ 30/1.1+30/1.1/1.1+30/1.1/1.1/1.1 = -17.9
例子2:某项目的现金流量如下,设 贴现率为 10%,则项目 NPV是多少?
期数 第0年 第1年 第2年 净现金流量 -630 330 440 解答:净现金流量 折算为现值 = -630 +330*1.1 +440*1.1*1.1 =34
例3:某项目利润预期如下,贴现率10%,计算 第三年结束时利润总额的NPV.
解答:净现值 = 11000/1.1+12100/1.21+13300/1.1/1.1/1.1 =30000
第1年 第2年 第3年 利润预期 11000 12100 13300
(2)投资回收期
定义:投资回收期 是指 项目从投产年算起, 用每年的净收益将初始投资全部 收回的时间。(收回全部投资所需的年限)又称投资返本期或 投资偿还年限,是投资收益率的倒数。
用于:评估项目或资产的投资回报情况。投资回收期计算公式可以帮助企业决策者更好地了解投资项目的盈利能力和风险水平,从而做出明智的决策。通常用年份来表示,投资回收期越短,说明项目回本的速度越快,风险越低。
公式:投资回收期 = 投资金额 / 年净现金流量,投资金额是指项目的总投资额,年净现金流量是指每年项目所产生的净现金流量。
静态投资回收期Pt =(T-1) + 第(T-1)年累计现金流量绝对值 / 第 T 年现金流量
动态投资回收期T =(T-1) + 第(T-1)年累计折现值 / 第 T 年折现值
(T:累计净现金流量开始出现正值的年份)
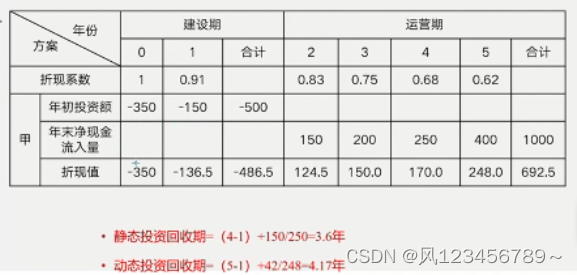
例子1:
例子2:
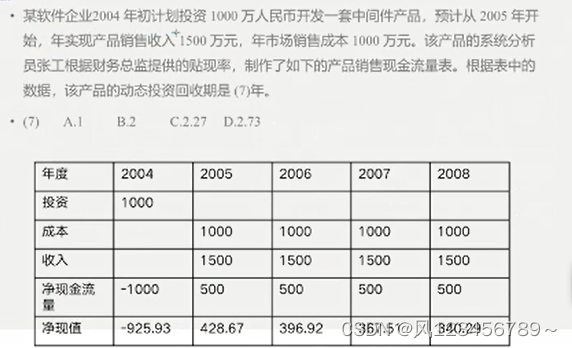
解答:动态 因此 需要看净现值,从2007开始 超了产出,(3-1)+(-925+428+396)/367=2.27
7.ROI 投资收益率分析
定义:投资收益率 ROI 是指 项目投产后,在运营正常年份获得的净收益与项目总投资之比。
投资收益率 ROI = (总的折现收益-总的折现成本)/折现成本 = 1/投资回收期
相关知识链接【项目管理专栏】文章清单
| 类别 | 文章 |
| 十大管理-文章 | 1 项目整合管理 项目管理 --项目整合管理(1/2)-CSDN博客 项目管理-项目整合管理2/2-CSDN博客 2 项目进度管理 项目管理-项目进度管理1/3-CSDN博客 项目管理-项目进度管理2/3-CSDN博客 项目管理-项目进度管理3/3-CSDN博客 3 项目范围管理 项目管理-项目范围管理1/2-CSDN博客 项目管理-项目范围管理2/2-CSDN博客 4 项目沟通管理 项目管理-项目沟通管理-CSDN博客 5 项目资源管理 项目管理-项目资源管理1/2-CSDN博客 6 项目采购管理 项目管理-项目采购管理1/2-CSDN博客 项目管理-项目采购管理2/2-CSDN博客 7 项目干系人管理 项目管理-干系人管理-CSDN博客 8 项目成本管理 项目管理-项目成本管理1/2-CSDN博客 项目管理-项目成本管理2/2-CSDN博客 9 项目风险管理 项目管理-项目风险管理1/3-CSDN博客 项目管理-项目风险管理2/3-CSDN博客 项目管理-项目风险管理3/3-CSDN博客 10项目质量管理 项目管理-项目质量管理-CSDN博客 |
| 相关知识 | 项目管理-项目绩效域1/2-CSDN博客 项目管理-配置管理与变更-CSDN博客 项目管理-项目管理科学基础-CSDN博客 项目管理-高级项目管理-CSDN博客 项目管理-相关知识(组织通用治理、组织通用管理、法律法规与标准规范)-CSDN博客 高项-案例分析万能答案(作业分享)-CSDN博客 |