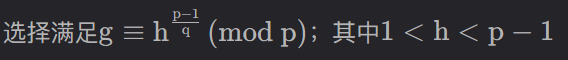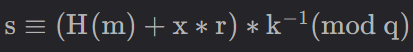一、历史

  1991年8月，NIST（Nation Institute of Standards and Technology，美国国家标准技术研究所）提出了数字签名算法（DSA）用于他们的数字签名标准（DSS）中。

DSA是算法，DSS是标准。标准采用算法，算法是标准的一部分。但是NIST的通告引起了大量谴责，这些谴责的政治性多于学术性。许多已经取得RSA算法专利许可权的大型软件公司也站出来反对DSS，他们已经投入大量的资金来实现RSA算法，他们当然不希望这些资金白白流失。 1994年5月19日，该标准最终颁布。

二、DSA算法的描述

  DSA是Schnorr和ElGamal签名算法的变形，该算法的安全性依赖于计算模数的离散对数的难度。

DSA签名中的公钥：

---

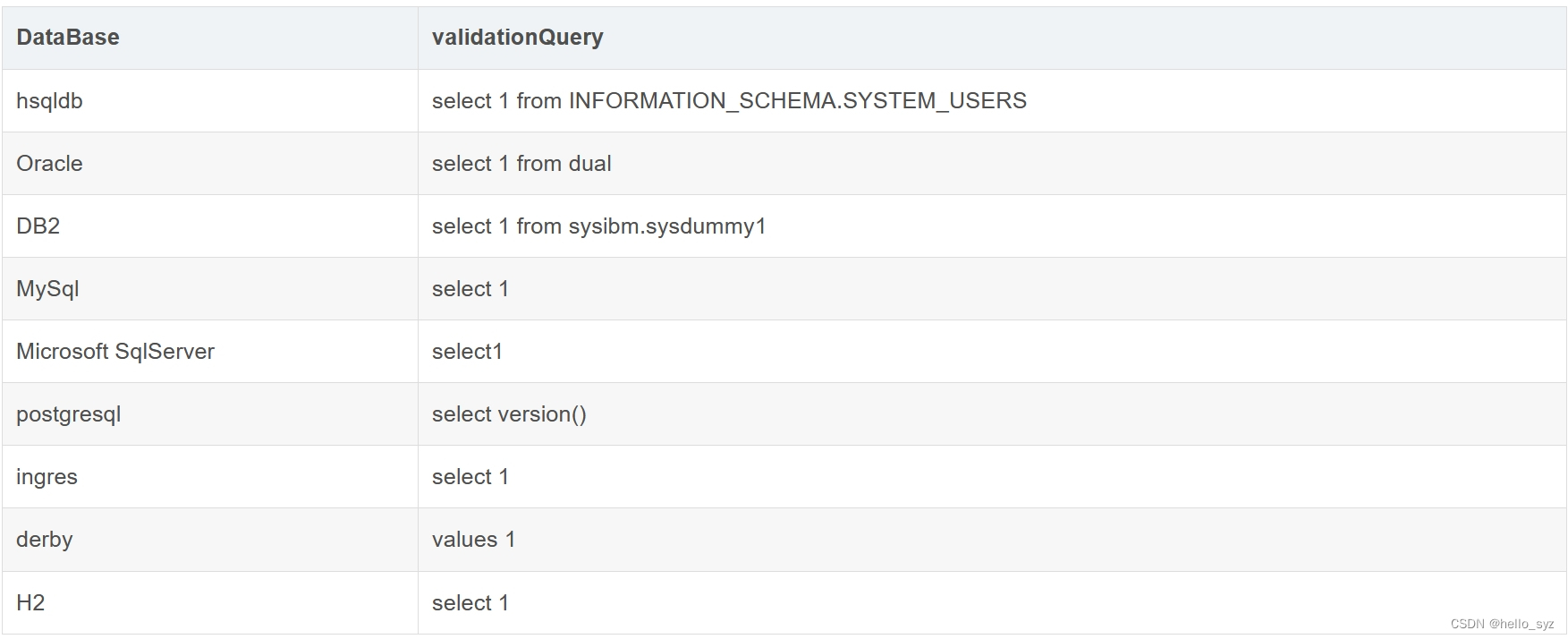
p	比特数为64 的倍数的素数,512~1024位的素数（可以在一组用户中共享）
q	160位长（这里对q qq的大小限制准确来说是不大于哈希函数H输出的长度），并与 p-1 互素的因子（可以在一组用户中共享）
	总之( p , q ) 的大小一般是( 1024 , 160 ) , ( 2048 , 224 ) , ( 2048 , 256 ) ，(3072,256),，单位比特
g
y

DSA签名中的私人密钥：

---

公钥为( p , q , g , y ) 私钥为( x )

DSA签名算法中的签名过程：

---

k选取小于q的随机数
r（签名）
s(签名)

签名结果为( r , s )

DSA签名算法中的验证过程：

---

对消息m签名时：

（1）Alice产生一个的随机数 k，k<q。 （2）Alice产生：        r = (gk mod p) mod q        s = （k-1 ( H(m)+xr )）mod q 其中，r 和 s 就是她的签名，她将它们发给 Bob。 （3）Bob通过计算来验证签名：        w = s-1 mod q        u1 = (H(m)×w) mod q        u2 = (rw) mod q        v = ((gu1 × yu2) mod p) mod q 如果， v=r，则签名有效。

三、 DSA的素数的产生

NIST在【1154】中推荐了一种产生素数 p 和q 的方法，其中 q 能整除 p-1。 素数 p 为 L 位，介于 512~1024 位，是 64 的倍数。 素数 q 为 160 位。 设 L-1=160n+6 （1）选取一个至少 160 位的任意序列，称为 S。设 g 是 S 的位长度。 （2）计算 U=SHA（S）⊕ SHA（（S+1）mod 2g），SHA是安全散列算法 （3）将U的 最高位 和 最低位 置为 1 形成 q （4）检验 q 是否是素数 （5）如果 q 不是素数，则回到（1） （6）设 C=0，N=2 （7）对 k=0,1，·······，n，令Vk = SHA（（S+N+k）mod 2g ） （8）令W=V0 + 2160V1+······+2160(n-1)Vn-1 + 2160n（Vn mod 2b），W为整数，且X=W+2L-1。注意 X 是 L 为长的数。 （9）令p=X-（（X mod 2q）-1）。注意 p 同余1 模 2q。 （10）若 p<2L-1，转到（13）步 （11）检测 p 是否为素数 （12）如果 p 是素数，转到（15）步 （13）令C=C+1，N=N+n+1 （14）如C=4096，转到第（1）步；否则，转到第（7）步 （15）将用于产生 p 和 q 的 S 和 C 值保存起来 在文献【1154】中，变量S称为“种子”，C称为“计数”，N称为“偏差” 单向散列函数SHA的使用能防止他人在背后做手脚。 这样做的安全性比RSA高，在RSA中，素数是秘密保存的。某人可能产生假素数或容易分解的特殊形式的素数，除非你知道私人密钥，否则你不知道这一点。而这里，即使你不知道私人密钥，你也可以确信 p 和 g 是随机产生的。

四、DSA的安全性

512位的DSA不能提供长期的安全性，但是1024位可以。

五、攻击k

  每个签名都需要一个新值 k，并且该值必须是随机选择的。 如果 Eve 恢复了 Alice 用来签名消息的 k，她就可以恢复 Alice 的私人密钥 x 。如果Eve获得了使用同一个 k 签名的两个消息，即使她不知道 k 的任何情况，也可以恢复 x 。拥有了 k ,Eve 就可以产生 Alice 的签名。在DSA实现中，一个好的随机数发生器对系统安全是至关重要的。

补充：可以使用DSA函数进行 ElGamal加密 和 RSA加密。

ECDSA

ECDSA是ECC与DSA的结合，整个签名过程与DSA类似，所不一样的是签名中采取的算法为ECC，最后签名出来的值也是分为r,s。

签名过程如下：

1、选择一条椭圆曲线Ep(a,b)，和基点G； 2、选择私有密钥k（k<n，n为G的阶），利用基点G计算公开密钥K=kG； 3、产生一个随机整数r（r<n），计算点R=rG； 4、将原数据和点R的坐标值x,y作为参数，计算SHA1做为hash，即Hash=SHA1(原数据,x,y)； 5、计算s≡r - Hash * k (mod n) 6、r和s做为签名值，如果r和s其中一个为0，重新从第3步开始执行

验证过程如下：

1、接受方在收到消息(m)和签名值(r,s)后，进行以下运算 2、计算：sG+H(m)P=(x1,y1), r1≡ x1 mod p。 3、验证等式：r1 ≡ r mod p。 4、如果等式成立，接受签名，否则签名无效。

重复利用K的后果：

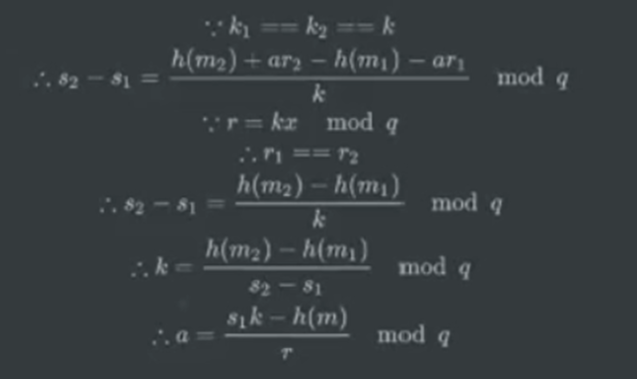
例题-蓝桥杯-signature

题目内容：

椭圆曲线数字签名算法，它利用椭圆曲线密码学（ECC）对数字签名算法（DSA）进行模拟，其安全性基于椭圆曲线离散对数问题。但是当某些数值相同时会出现一些安全问题。

题目代码

import ecdsa
import random
​
def ecdsa_test(dA,k):
​
    sk = ecdsa.SigningKey.from_secret_exponent(
        secexp=dA,
        curve=ecdsa.SECP256k1
    )
    sig1 = sk.sign(data=b'Hi.', k=k).hex()
    sig2 = sk.sign(data=b'hello.', k=k).hex()
​
    r1 = int(sig1[:64], 16)
    s1 = int(sig1[64:], 16)
    s2 = int(sig2[64:], 16)
    return r1,s1,s2
​
if __name__ == '__main__':
    n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
    a = random.randint(0,n)
    flag = 'flag{' + str(a) + "}"
    b = random.randint(0,n)
    print(ecdsa_test(a,b))
​
# (4690192503304946823926998585663150874421527890534303129755098666293734606680, 111157363347893999914897601390136910031659525525419989250638426589503279490788, 74486305819584508240056247318325239805160339288252987178597122489325719901254)

分析代码可以看出，存在随机数重复使用。具体来说，这段代码中签名的过程中使用了相同的随机数 k 来对不同的消息进行签名。这种情况下，可以通过分析两个相同 k 值对应的消息签名来恢复私钥 dA。

在 ECDSA 中，每次签名过程中都会使用一个随机数 k，以确保生成唯一的签名。然而，如果相同的随机数 k 被重复使用来对不同的消息进行签名，攻击者就有可能通过数学分析和推导计算出私钥 dA。

解密脚本

import sympy
from hashlib import sha1
from Cryptodome.Util.number import long_to_bytes , bytes_to_long
​
​
def calculate_private_key(r1, s1, s2, h1, h2, n):
    # 计算k值
    k = ((h1 - h2) * sympy.mod_inverse(s1 - s2, n)) % n
    # 计算私钥dA
    dA = (sympy.mod_inverse(r1, n) * (k * s1 - h1)) % n
    return dA
​
​
​
if __name__ == "__main__":
    # 定义椭圆曲线的参数
    n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
    # 签名中的r1, s1, s2值
    r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680
    s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788
    s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254
    h1 = bytes_to_long(sha1(b'Hi.').digest())
    h2 = bytes_to_long(sha1(b'hello.').digest())
    private_key = calculate_private_key(r1, s1, s2, h1, h2, n)
    print(f'flag{{{private_key}}}')
​
# flag{40355055231406097504270940121798355439363616832290875140843417522164091270174}
椭圆曲线密码中的签名整数k相同攻击利用。

因为k值相同，所以r值也是相同的。

题目中给到了使用相同的k进行两次签名的结果，那根据：

s1 = k^-1 (z1 + rda) mod n
s2 = k^-1 (z2 + rda) mod n
s1 - s2 = k^-1 (z1 - z2) mod n
K = (s1-s2)^-1 * (z1 -z2) mod n
得到k，最后再代入原式便能解出da了，即本题中的flag，完整exp：

from gmpy2 import *
from Crypto.Util.number import *
from hashlib import *
​
n= 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
​
r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680
r2 = 4690192503304946823926998585663150874421527890534303129755098666293734606680
s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788
s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254
 
z1 = sha1(b'Hi.').digest()
z2 = sha1(b'hello.').digest()
s1_1 = inverse(s1, n)
s2_1 = inverse(s2, n)
​
def check(key):
    for i in range(len(key)):
        if key[i] < 32 or key[i] > 127:
            return 0
    return 1
 
x = (s2_1*bytes_to_long(z2) - s1_1*bytes_to_long(z1))%n
key = x*inverse(s1_1*r1-s2_1*r2, n)%n
​
print(key)