leetcode刷题：买卖股票的最佳时机

news2024/11/27 16:29:07

题目

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1

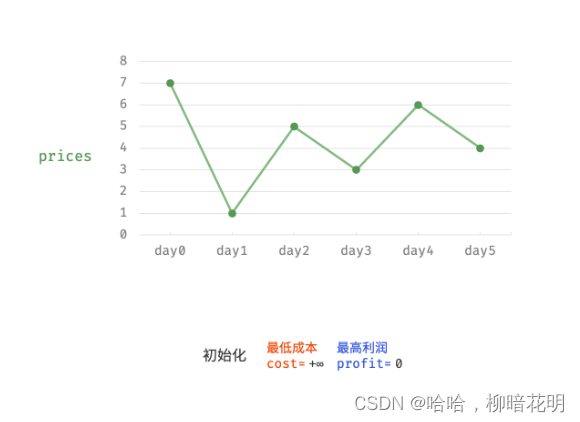
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示

1 <= prices.length <= $10^5$
0 <= prices[i] <= $10^4$

解题思路

先考虑最简单的「暴力遍历」，即枚举出所有情况，并从中选择最大利润。设数组 prices 的长度为 n ，由于只能先买入后卖出，因此第 1 天买可在未来 n−1 天卖出，第 2 天买可在未来 n−2天卖出……以此类推，共有 (n−1)+(n−2)+⋯+0=n(n-1)/2种情况，时间复杂度为 O( $N^2$ )
) 。考虑到题目给定的长度范围 1≤prices.length≤ $10^5$ ，需要思考更优解法。

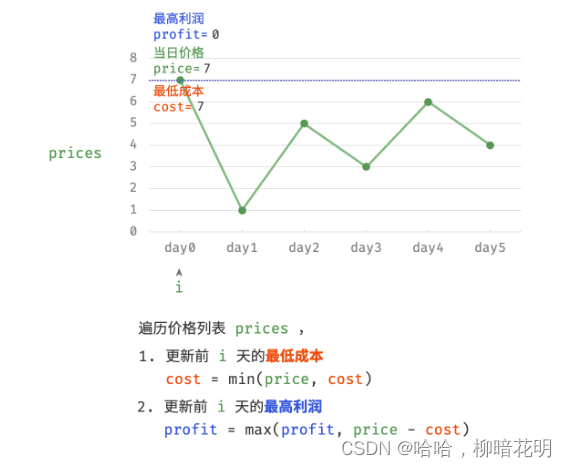
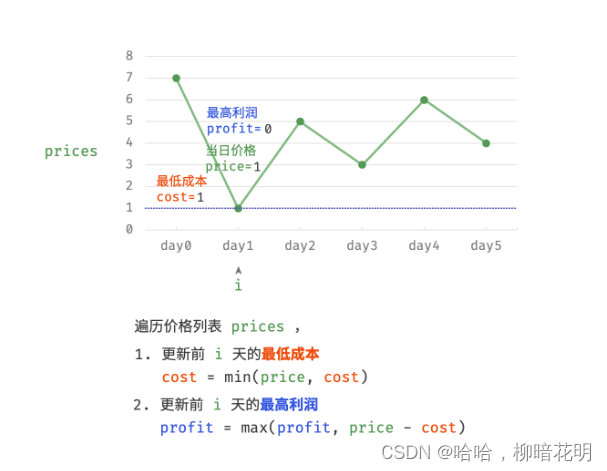
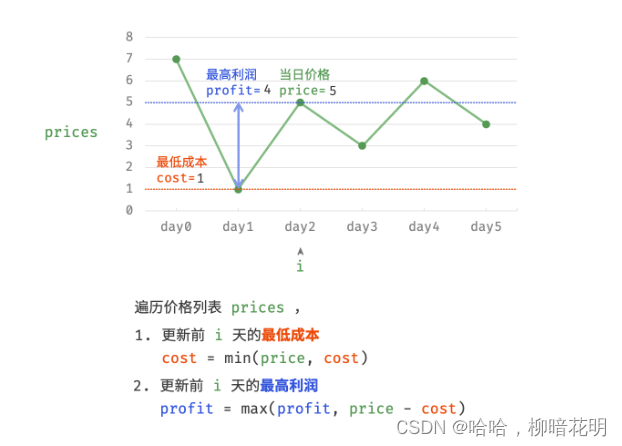
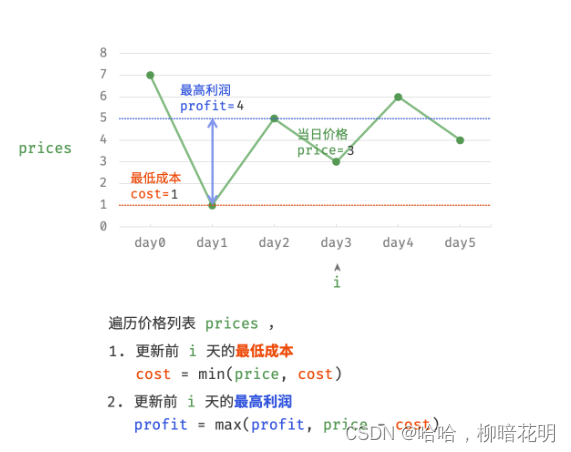
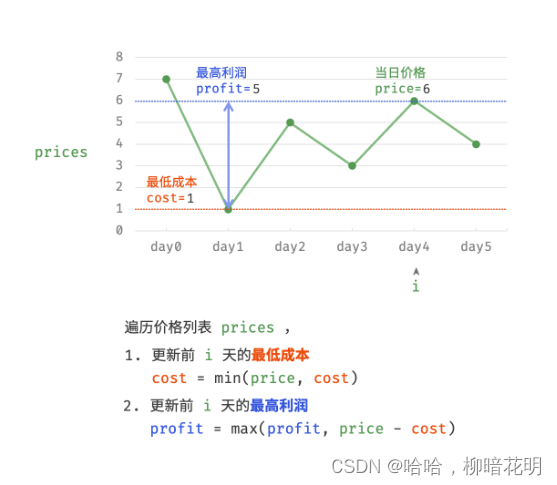
因为，暴力法会产生许多冗余计算。例如，若第 1 天价格低于第 2 天价格，即第 1 天成本更低，那么我们一定不会选择在第 2 天买入。进一步的，若在前 i天选择买入，若想达到最高利润，则一定选择价格最低的交易日买入。考虑根据此贪心思想，遍历价格列表 prices 并执行两步：

由于初始值 i=0 ，为了序号对应，本文设从第 0 天开始；

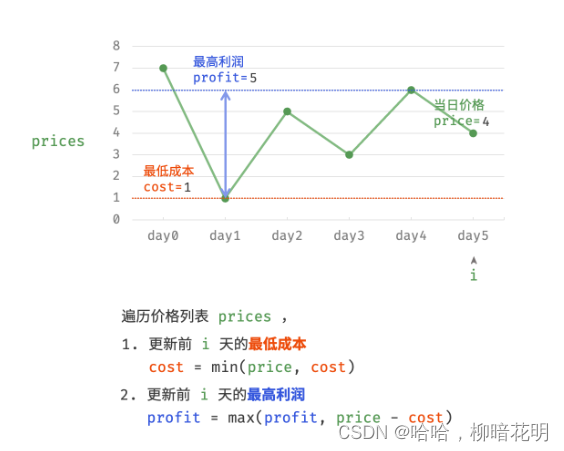
更新前 i天的最低价格，即最低买入成本 cost；
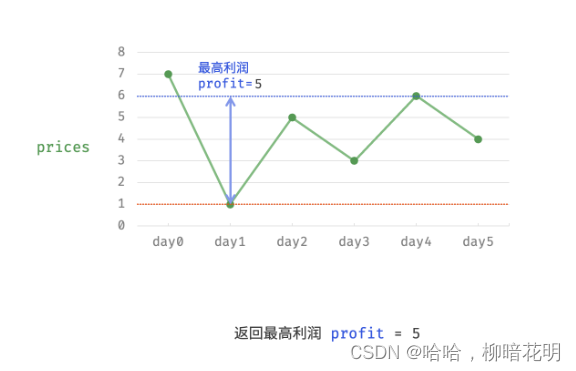
更新前 i天的最高利润 profit ，即选择「前 i−1天最高利润 profit 」和「第 i 天卖出的最高利润 price - cost 」中的最大值。

class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE, profit = 0;
        for (int price : prices) {
            cost = Math.min(cost, price);
            profit = Math.max(profit, price - cost);
        }
        return profit;
    }
}

复杂度分析

时间复杂度 O( $N$ ) ：其中 N 为数组 prices 长度。遍历 prices 使用线性时间。
空间复杂度 O( $1$ ) ：变量 cost , profit 使用 O( $1$ ) 空间。

关于动态规划

动态规划（Dynamic Programming，简称 DP）是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。动态规划方法的基本思想是：将待求解的问题分解成若干个相互重叠的子问题，求解一个子问题时，将其解存储起来，以便以后利用。这样，在求解任何一个子问题时，所利用的子问题的解都是已经计算过的，从而避免了重复计算。

以下是动态规划的一些基本步骤：

描述最优解的结构：如果问题的最优解包含了其子问题的最优解，则称该问题具有最优子结构性质。动态规划利用这一性质，通过求解子问题的最优解来构造原问题的最优解。
定义状态：状态就是原问题和子问题的解。状态必须能够表示出与原问题相关的所有信息，从而能够推导出子问题的解。
状态转移方程：状态转移方程就是描述状态之间关系的方程。它表示了如何从子问题的最优解推导出原问题的最优解。
计算最优解：按照状态转移方程，从子问题的最优解开始，逐步推导出原问题的最优解。

下面是一个经典的动态规划问题——背包问题的例子：

给定一组物品，每种物品都有自己的重量和价值。在限定的总重量内，我们如何选择，才能使得物品的总价值最高。这就是一个典型的背包问题。我们可以使用动态规划来解决这个问题。首先，我们定义状态 dp[i][j] 表示在前 i 个物品中，选择总重量不超过 j 的物品，能够得到的最大价值。然后，我们可以得到状态转移方程：

如果第 i 个物品的重量大于 j，那么 dp[i][j] = dp[i-1][j]，即前 i 个物品的最大价值等于前 i-1 个物品的最大价值（因为第 i 个物品太重，无法放入背包）。
否则，dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])。这里有两种选择：要么不选第 i 个物品，此时最大价值为 dp[i-1][j]；要么选择第 i 个物品，此时最大价值为前 i-1 个物品在总重量不超过 j-weight[i] 的情况下的最大价值加上第 i 个物品的价值。