C++——二叉树搜索树

news2025/11/4 9:58:17

前面写了初阶数据结构——二叉树；本文内容是来对它来进行结尾

目录

一概念

二实现

2.1查找

2.2插入 

2.3删除

完整源代码

三二叉树的应用 

 四二叉搜索树的性能分析

 五二叉搜索树相关的面试题

一概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

*  若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
** 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
***它的左右子树也分别为二叉搜索树

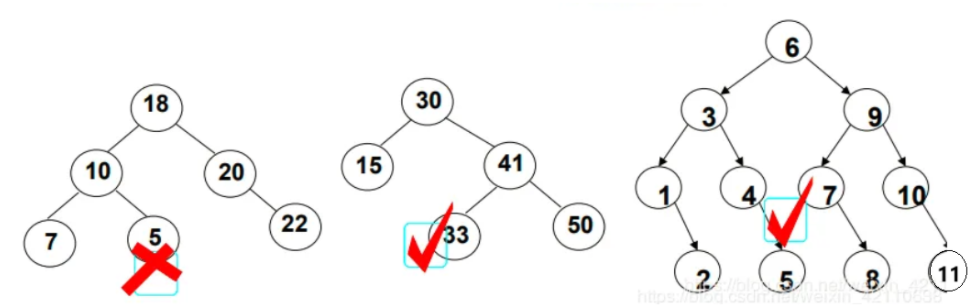
二实现

以下面的二叉搜索树为例：

2.1查找

a、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
b、走到到空，还没找到，这个值不存在。

bool find(const K& val)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < val)
		{
			cur = cur->_right;
		}
		else if (cur->_key > val)
		{
			cur = cur->_left;
		}
		else
		{
			//相等
			return true;
		}
	}
	return false;
}

2.2插入 

a. 树为空，则直接新增节点，赋值给root指针
b. 树不空，按二叉搜索树性质查找插入位置，插入新节点

bool insert(const K& val)
{
	if (_root == nullptr)
	{
		_root = new Node(val);
		return true;
	}
	else
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < val)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > val)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//相等
				return false;
			}
		}
		//判断要在parent的左还是右进行插入
		cur = new Node(val);
		if (parent->_key > val)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		return true;
	}
}

2.3删除

a先通过二叉搜索树的性质找到节点的位置

b分析删除节点的左右孩子的情况：

无左右孩子节点(不考虑)

只有左孩子节点：删除之前把左孩子交给父亲节点

只有右孩子节点：删除之前把右孩子交给父亲节点

右孩子节点都有：有两种解决方法：

1找左节点的最大值的节点Max:Max的val与待删除的val进行交换；

2找右孩子的最小值的节点Min:Min的val与待删除的val进行交换；

以第二种为例来设计代码：

要注意对特殊情况的处理(删除根节点的情况)：

 

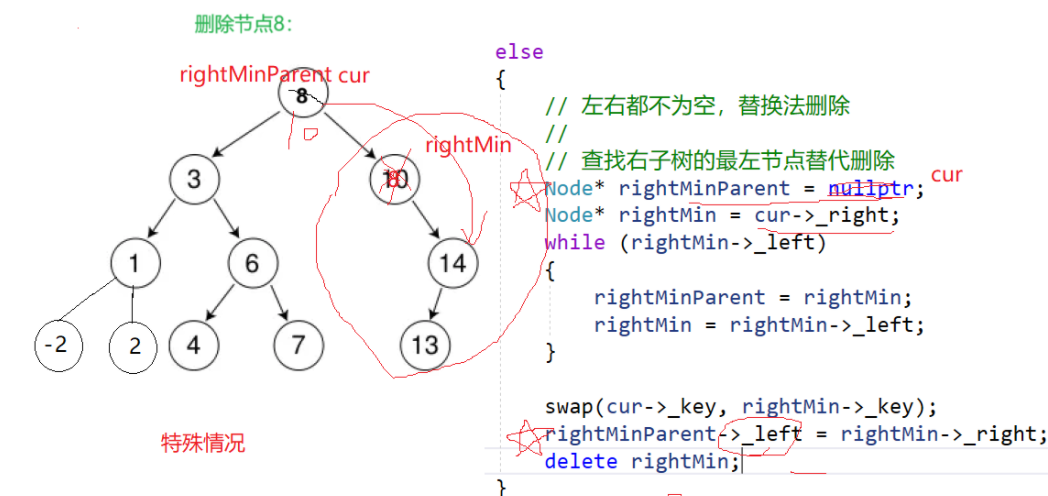
特别要记录cur(删除节点)的父节点(cur在父节点的左边还是右边不清楚) 

bool erase(const K& val)
{
	if (_root == nullptr) return false;
	Node* parent = nullptr;
	Node* cur = _root;

	while (cur)
	{
		if (cur->_key < val)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > val)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			//找到删除位置
			//右孩子为空
			if (cur->_right == nullptr)
			{
				//cur是根节点
				if (parent == nullptr) _root = cur->_left;
				//cur的左孩子交给parent
				else
				{
					if (parent->_left == cur) parent->_left = cur->_left;
					else if (parent->_right == cur) parent->_right = cur->_left;
				}
				delete cur;
			}
			//右孩子为空
			else if (cur->_left == nullptr)
			{
				//cur==_root
				if (parent == nullptr) _root = cur->_right;
				else
				{
					if (parent->_left == cur) parent->_left = cur->_right;
					else if (parent->_right == cur) parent->_right = cur->_right;
				}
				delete cur;
			}
			//都有
			else
			{
				//找到右节点的最小值进行替换删除（左节点的最大值）

				//要删除的可能是_root patent不能为nullptr
				Node* ParentRightMin = cur;
				Node* RightMin = cur->_right;
				while (RightMin->_left)
				{
					ParentRightMin = RightMin;
					RightMin = RightMin->_left;
				}

				swap(RightMin->_key, cur->_key);

				//RightMin的右子树交给ParentRightMin
				if (ParentRightMin->_right == RightMin)
				{
					ParentRightMin->_right = RightMin->_right;
				}
				else
				{
					ParentRightMin->_left = RightMin->_right;
				}

				delete RightMin;
			}
			return true;
		}
	}
	return false;
}

完整源代码


#pragma once
#include<iostream>
using namespace std;

namespace bit
{
	template<class K>
	struct Node
	{
		Node(const K& key = K())
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}

		Node<K>* _left;
		Node<K>* _right;
		K _key;
	};
	template<class K>
	class BSTree
	{
		typedef Node<K> Node;
	public:
	
		bool insert(const K& val)
		{
			if (_root == nullptr)
			{
				_root = new Node(val);
				return true;
			}
			else
			{
				Node* parent = nullptr;
				Node* cur = _root;
				while (cur)
				{
					if (cur->_key < val)
					{
						parent = cur;
						cur = cur->_right;
					}
					else if (cur->_key > val)
					{
						parent = cur;
						cur = cur->_left;
					}
					else
					{
						//相等
						return false;
					}
				}
				//判断要在parent的左还是右进行插入
				cur = new Node(val);
				if (parent->_key > val)
				{
					parent->_left = cur;
				}
				else
				{
					parent->_right = cur;
				}
				return true;
			}
		}

		bool find(const K& val)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < val)
				{
					cur = cur->_right;
				}
				else if (cur->_key > val)
				{
					cur = cur->_left;
				}
				else
				{
					//相等
					return true;
				}
			}
			return false;
		}

		bool erase(const K& val)
		{
			if (_root == nullptr) return false;
			Node* parent = nullptr;
			Node* cur = _root;

			while (cur)
			{
				if (cur->_key < val)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > val)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					//找到删除位置
					//右孩子为空
					if (cur->_right == nullptr)
					{
						//cur是根节点
						if (parent == nullptr) _root = cur->_left;
						//cur的左孩子交给parent
						else
						{
							if (parent->_left == cur) parent->_left = cur->_left;
							else if (parent->_right == cur) parent->_right = cur->_left;
						}
						delete cur;
					}
					//右孩子为空
					else if (cur->_left == nullptr)
					{
						//cur==_root
						if (parent == nullptr) _root = cur->_right;
						else
						{
							if (parent->_left == cur) parent->_left = cur->_right;
							else if (parent->_right == cur) parent->_right = cur->_right;
						}
						delete cur;
					}
					//都有
					else
					{
						//找到右节点的最小值进行替换删除（左节点的最大值）

						//要删除的可能是_root patent不能为nullptr
						Node* ParentRightMin = cur;
						Node* RightMin = cur->_right;
						while (RightMin->_left)
						{
							ParentRightMin = RightMin;
							RightMin = RightMin->_left;
						}

						swap(RightMin->_key, cur->_key);

						//RightMin的右子树交给ParentRightMin
						if (ParentRightMin->_right == RightMin)
						{
							ParentRightMin->_right = RightMin->_right;
						}
						else
						{
							ParentRightMin->_left = RightMin->_right;
						}

						delete RightMin;
					}
					return true;
				}
			}
			return false;
		}

		//进行套壳
		void _InOrder()
		{
			InOrder(_root);
			cout << endl;
		}

	private:
		void InOrder(const Node* _root)
		{
			if (_root == nullptr) return;
			InOrder(_root->_left);
			cout << _root->_key << " ";
			InOrder(_root->_right);
		}
	private:
		Node* _root=nullptr;
	};

	void Test1()
	{
		BSTree<int> sb;
		sb.insert(3);
		sb.insert(2);
		sb.insert(4);
		sb._InOrder();
		sb.erase(3);
		sb.erase(2);
		sb.erase(4);
		sb._InOrder();
	}
}

三二叉树的应用 

KV模型：

每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方式在现实生活中非常常见：
比如：英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英
文单词与其对应的中文<word, chinese>就构成一种键值对：

//对二叉搜索树进行改造：
template<class K,class V>
struct Node
{
	Node(const K& key = K(),const V& val=V())
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
		,_val(val)
	{}

	Node<K,V>* _left;
	Node<K,V>* _right;
	K _key;
	V _val;
};
template<class K,class V>
class BSTree
{
	typedef Node<K,V> Node;
public:

	bool Insert(const K& val,const K& valute)
	{
		if (_root == nullptr)
		{
			_root = new Node(val,valute);
			return true;
		}
		else
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < val)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > val)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					//相等
					return false;
				}
			}
			//判断要在parent的左还是右进行插入
			if (parent->_key > val)
			{
				parent->_left = new Node(val,valute);
			}
			else
			{
				parent->_right = new Node(val,valute);
			}
			return true;
		}
	}

	Node* Find(const V& val)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < val)
			{
				cur = cur->_right;
			}
			else if (cur->_key > val)
			{
				cur = cur->_left;
			}
			else
			{
				//相等
				return cur;
			}
		}
		return nullptr;
	}
	void _InOrder()
	{
		InOrder(_root);
	}

private:
	void InOrder(const Node* _root)
	{
		if (_root == nullptr) return;
		InOrder(_root->_left);
		cout << _root->_key << endl;
		InOrder(_root->_right);
	}
	Node* _root = nullptr;
};

void Test1()
{
	// 输入单词，查找单词对应的中文翻译
	BSTree<string, string> dict;
	dict.Insert("string", "字符串");
	dict.Insert("tree", "树");
	dict.Insert("left", "左边、剩余");
	dict.Insert("right", "右边");
	dict.Insert("sort", "排序");
	// 插入词库中所有单词
	string str;
	while (cin >> str)
	{
		Node<string, string>* ret = dict.Find(str);
		if (ret == nullptr)
		{
			cout << "单词拼写错误，词库中没有这个单词:" << endl;
		}
		else
		{
			cout << "中文翻译:" << ret->_val << endl;
		}
	}
}

 四二叉搜索树的性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。 

但二叉搜索树在不同的场景可能会有以下结构：

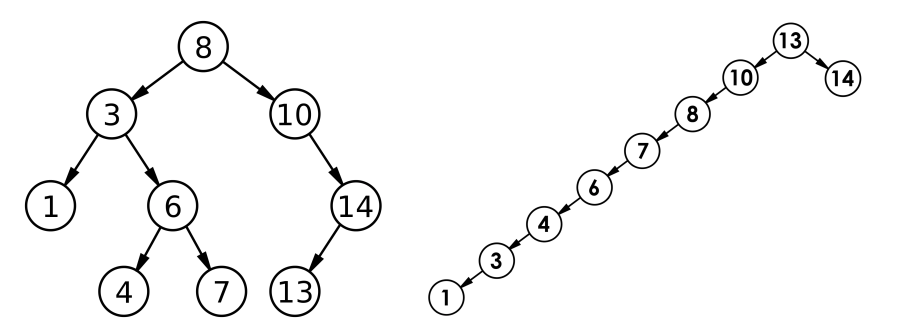
最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：long2N
最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为：N方

而在这种最差的情况下是有办法去去对它进行调整：将二叉树进行旋转，这个我们下文在说

 五二叉搜索树相关的面试题

 1. 二叉树创建字符串。oj链接
2. 二叉树的分层遍历1。oj链接
3. 二叉树的分层遍历2。oj链接
4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。oj链接
5. 二叉树搜索树转换成排序双向链表。oj链接
6. 根据一棵树的前序遍历与中序遍历构造二叉树。 oj链接
7. 根据一棵树的中序遍历与后序遍历构造二叉树。oj链接
8. 二叉树的前序遍历，非递归迭代实现 。oj链接
9. 二叉树中序遍历 ，非递归迭代实现。oj链接
10. 二叉树的后序遍历 ，非递归迭代实现。oj链接

以上便是我在学习二叉搜索树的相关内容，有错误欢迎在评论区指正，谢谢！！ 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1668138.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

牛津大学和上海交大将SAM和Flow应用于移动目标，简单而有效，轻松分割运动目标！

牛津大学和上海交大将SAM和Flow应用于移动目标，简单而有效，轻松分割运动目标！

光流可以在运动物体分割中发现运动物体并为分割提供清晰的边界。然而&#xff0c;如果物体暂时静止&#xff0c;就会面临分割挑战。 而我们知道SAM可以很好的分割静态图像对象。因此&#xff0c;是否可以利用SAM与光流结合来在视频中进行移动物体分割&#xff1f; 今天给大家介…
阅读更多...
开源web在线数据库设计软件 —— 筑梦之路

开源web在线数据库设计软件 —— 筑梦之路

GitHub - drawdb-io/drawdb: Free, simple, and intuitive online database design tool and SQL generator. 简介 DrawDB是一款多功能且用户友好的在线工具&#xff0c;允许用户轻松设计数据库实体关系。通过简单直观的界面&#xff0c;DrawDB使用户能够创建图表、导出SQL脚本…
阅读更多...
Spring6 的JdbcTemplate的JDBC模板类的详细使用说明

Spring6 的JdbcTemplate的JDBC模板类的详细使用说明

1. Spring6 的JdbcTemplate的JDBC模板类的详细使用说明 文章目录 1. Spring6 的JdbcTemplate的JDBC模板类的详细使用说明每博一文案2. 环境准备3. 数据准备4. 开始4.1 从数据表中插入(添加)数据4.2 从数据表中修改数据4.3 从数据表中删除数据4.4 从数据表中查询一个对象4.5 从数…
阅读更多...
kafka安装及收发消息

kafka安装及收发消息

kafka需要与zookeeper配合使用&#xff0c;但是从2.8版本kafka引入kraft&#xff0c;也就是说在2.8后&#xff0c;zookeeper和kraft都可以管理kafka集群&#xff0c;这里我们依然采用zookeeper来配合kafka。 1、首先我们下载zookeeper 下载地址为 https://zookeeper.apache.org…
阅读更多...
openlayers实现绘制图标，并实现图标的聚合功能

openlayers实现绘制图标，并实现图标的聚合功能

点聚合说明 点聚合功能是指将地图上密集的点数据聚合成一个更大的点或者其他形状&#xff0c;以改善地图的可视化效果和性能。点聚合功能通常用于在地图上显示大量的点标记&#xff0c;例如地图上的POI&#xff08;兴趣点&#xff09;、传感器数据等。通过点聚合功能&#xff…
阅读更多...
【机器学习300问】86、简述超参数优化的步骤？如何寻找最优的超参数组合？

【机器学习300问】86、简述超参数优化的步骤？如何寻找最优的超参数组合？

本文想讲述清楚怎么样才能选出最优的超参数组合。关于什么是超参数&#xff1f;什么是超参数组合&#xff1f;本文不赘述&#xff0c;在之前我写的文章中有详细介绍哦&#xff01; 【机器学习300问】22、什么是超参数优化&#xff1f;常见超参数优化方法有哪些&#xff1f;htt…
阅读更多...
[Bug]：由于中国防火墙，无法连接 huggingface.co

[Bug]：由于中国防火墙，无法连接 huggingface.co

问题描述 ： OSError: We couldnt connect to https://huggingface.co to load this file, couldnt find it in the cached files and it looks like youscan/ukr-roberta-base is not the path to a directory containing a file named config. Json. Checkout your internet …
阅读更多...
支持视频切片的开源物联网平台

支持视频切片的开源物联网平台

软件介绍 MzMedia开源视频联动物联网平台是一个简单易用的系统,该平台支持主流短视频平台&#xff08;如抖音、快手、视频号&#xff09;的推流直播功能&#xff0c;同时提供视频切片等功能。系统后端采用Spring Boot&#xff0c;前端采用Vue3和Element Plus&#xff0c;消息服…
阅读更多...
[C++初阶]string的几道oj题

[C++初阶]string的几道oj题

1.LCR 192. 把字符串转换成整数 (atoi) 这题难度不大,我这里采取遍历跳过空格的方式&#xff0c;我先展示出我的代码,然后慢慢讲解: class Solution { public:int myAtoi(string str) {if (str.empty()) return 0;int lengthstr.size();int i0;int symbol1;int sum0;while(i&l…
阅读更多...
C++组合类

C++组合类

类的数据成员不但可以是基本类型&#xff0c;也可以是其它类的对象。 组合类就是指一个类包含其他类的对象作为该类的数据成员。 当组合类创建对象时&#xff0c;其中包含的各个数据成员对象应首先被创建。因此&#xff0c;在创建类的对象时&#xff0c;既要对本类的基本…
阅读更多...
2024小红书电商实战营，养号打造IP/选爆品/开店铺/爆款笔记/等等（24节）

2024小红书电商实战营，养号打造IP/选爆品/开店铺/爆款笔记/等等（24节）

我们非常荣幸地为大家带来2024小红书电商实战营的第一期&#xff0c;在这里我们将带领大家一起深入学习如何利用小红书平台&#xff0c;实现个人品牌的发展和商业利益的增长。 首先&#xff0c;我们将讨论养号的重要性以及如何打造个人品牌。无论是建立自己的受众群体还是提高…
阅读更多...
java基础知识点总结2024版（8万字超详细整理）

java基础知识点总结2024版（8万字超详细整理）

java基础知识点总结2024版&#xff08;超详细整理&#xff09; 这里写目录标题 java基础知识点总结2024版&#xff08;超详细整理&#xff09;java语言的特点1.简单性2.面向对象3.分布式4.健壮性5.安全性6.体系结构中立7.可移植性8.解释性9.多线程10.动态性 初识java中的main方…
阅读更多...
刨析YOLOv8的改进模块

刨析YOLOv8的改进模块

1、YOLOv5回顾 这里粗略回顾一下，这里直接提供YOLOv5的整理的结构图吧：Backbone：CSPDarkNet结构，主要结构思想的体现在C3模块，这里也是梯度分流的主要思想所在的地方；PAN-FPN：双流的FPN，必须香，也必须快，但是量化还是有些需要图优化才可以达到最优的性能，比如cat前后…
阅读更多...
【机器学习300问】87、学习率这种超参数在优化时选择随机搜索方法，为什么要在对数尺度范围进行随机搜索？

【机器学习300问】87、学习率这种超参数在优化时选择随机搜索方法，为什么要在对数尺度范围进行随机搜索？

在超参数优化过程中&#xff0c;对数尺度范围进行随机采样对于某些类型的超参数来说是非常有效的&#xff0c;特别是当超参数的有效值跨越几个数量级时。学习率就是这样一种超参数&#xff0c;它可以从非常小&#xff08;例如&#xff09;到相对大的值&#xff08;例如&#xf…
阅读更多...
Java RMI SERVER命令执行漏洞

Java RMI SERVER命令执行漏洞

Java RMI SERVER命令执行漏洞 一、介绍二、原理三、复现准备四、漏洞复现 一、介绍 RMI全称是Remote Method Invocation&#xff08;远程方法调用&#xff09;&#xff0c;是专为Java环境设计的远程方法调用机制&#xff0c;远程服务器提供API&#xff0c;客户端根据API提供相…
阅读更多...
57. 【Android教程】相机：Camera

57. 【Android教程】相机：Camera

相机现在已经不仅仅是手机必备神器了&#xff0c;甚至相机的拍照质量已经是很多人买手机的首选条件了。而对于相机而言主要有两大功能&#xff1a;拍照片和拍视频。Android 为此两种方式&#xff1a; 相机 intent相机 API 本节我们就一起来看看相机的具体用法。 1. 打开 Camer…
阅读更多...
STC8增强型单片机开发day03

STC8增强型单片机开发day03

中断系统INT 中断的概念 中断系统是为使 CPU 具有对外界紧急事件的实时处理能力而设置的。 当中央处理机 CPU 正在处理某件事的时候外界发生了紧急事件请求&#xff0c;要求 CPU 暂停当前的工作,转而去处理这个紧急事件&#xff0c;处理完以后&#xff0c;再回到原来被中断的…
阅读更多...
鸿蒙内核源码分析(共享内存) | 进程间最快通讯方式

鸿蒙内核源码分析(共享内存) | 进程间最快通讯方式

运行机制 共享好端端的一词&#xff0c;近些年被玩坏了&#xff0c;共享单车,共享充电宝,共享办公室&#xff0c;共享雨伞… 甚至还有共享女朋友&#xff0c;真是人有多大胆&#xff0c;共享有多大产。但凡事太尽就容易恶心到人&#xff0c;自己也一度被 共享内存 恶心到了&am…
阅读更多...
南京信工一班IP(2)

南京信工一班IP(2)

第六章&#xff0c;BGP—边界网关协议 自治系统—AS ​ 定义&#xff1a;由一个单一的机构或组织所管理的一系列IP网络及其设备所构成的集合。 ​ AS的来源&#xff1a; 整个网络规模过大&#xff0c;会导致路由信息收敛速度过慢&#xff0c;设备对相同目标认知不同。AS之间…
阅读更多...
python算法demo0512

python算法demo0512

最长回文数 代码 class Solution:def longestPalindrome(self, s: str) -> str:n len(s)if n < 2:return smax_len 1begin 0# dp[i][j] 表示 s[i..j] 是否是回文串dp [[False] * n for _ in range(n)]for i in range(n):dp[i][i] True# 递推开始# 先枚举子串长度fo…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023