1.应用：
1.在工业上的应用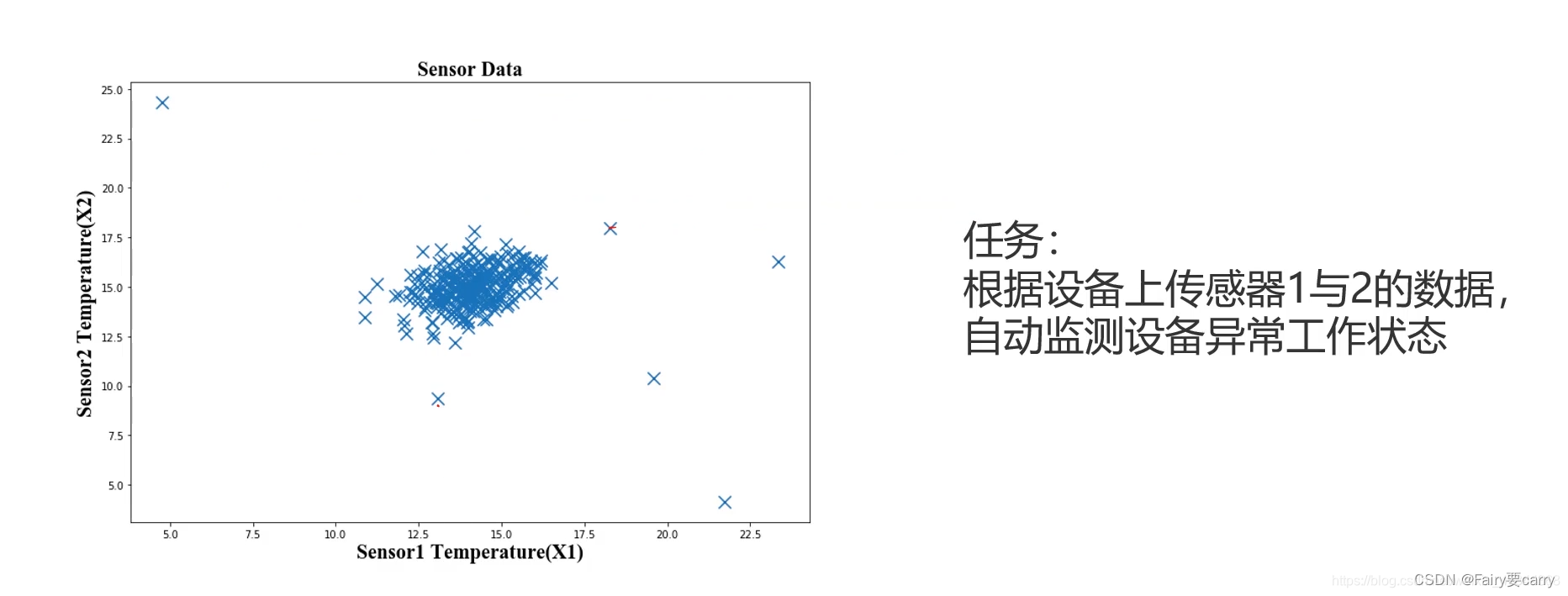
当检测设备是否处于异常工作状态时，可以由上图分析得到：那些零散的点对应的数据是异常数据。因为设备大多数时候都是处于正常工作状态的，所以数据点应该比较密集地集中在一个范围内，而那些明显偏出正常范围内的数据点就是我们要找的异常数据了，此时就可以自动
2.在图像里的应用
通过异常检测，我们也可以检测到图像中的异常图像。（如上图中的小红鱼）
此外，异常检测的应用还有很多，比如：
异常消费检测（商业）
缺陷基因检测（医疗）
劣质产品检测（工业）等等
2.对于异常检测的定义：
根据输入的数据，对不符合预期模式的数据进行识别
3.介绍：
假设我们有一个一维的数据集，在这个数据集中有m个样本：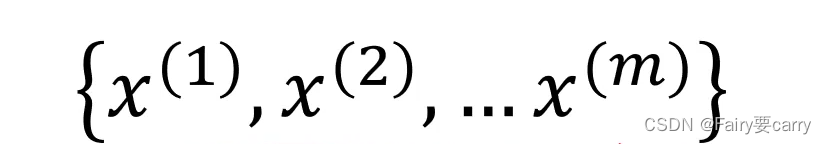
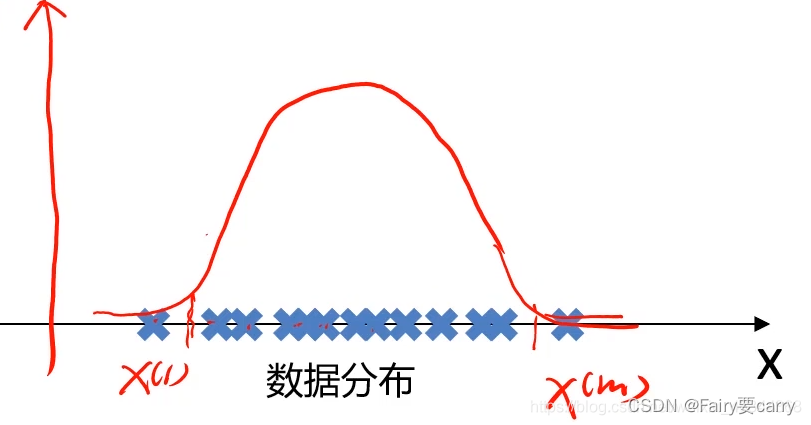
数据在x轴的分别如下图：
我们的目标是自动地找出这上面的异常样本，就可以根据样本在坐标轴上分布的数量多少，计算出坐标轴上各点对应的样本的概率密度，可以设定当概率密度小于某个值时，这时其对应的样本就是我们要找的异常样本。——>根据各个样本对应的概率函数计算出来的值画出数据分布，进而判断是否属于异常样本
这里说一下高斯分布的概率密度函数：
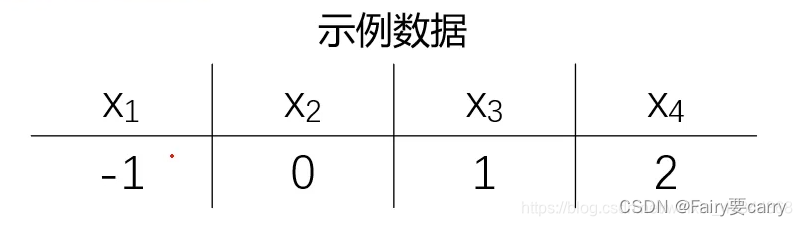
根据以上数据我们就可以计算出我们的均值和方差：
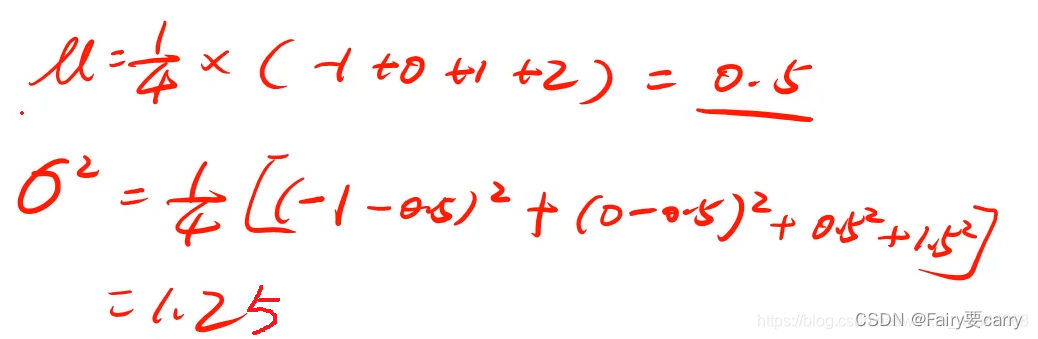
然后我们将均差和方差带入公式就能算出我们的P(x)了：
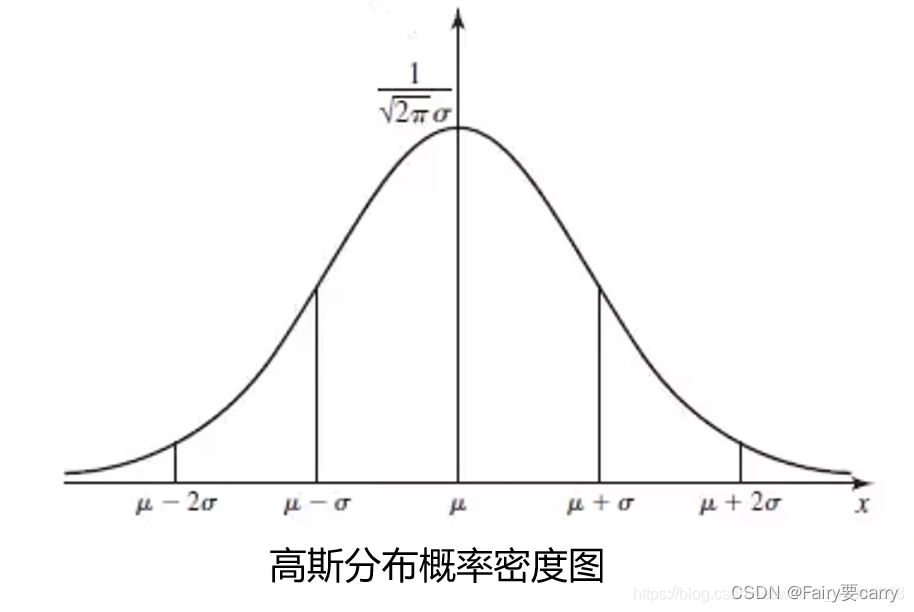
4.如何根据高斯分布概率去解决异常检测的问题呢？
**（第一步）**在我们知道X1、X2……Xm这些数据后，就可以进行相应计算了。
- 计算各个数据均值u,标准差σ
- 计算对应的高斯分布概率密度函数P(x)
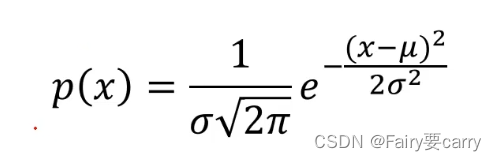
（第二步）计算出来后，数据对应的高斯分布概率密度函数如下图
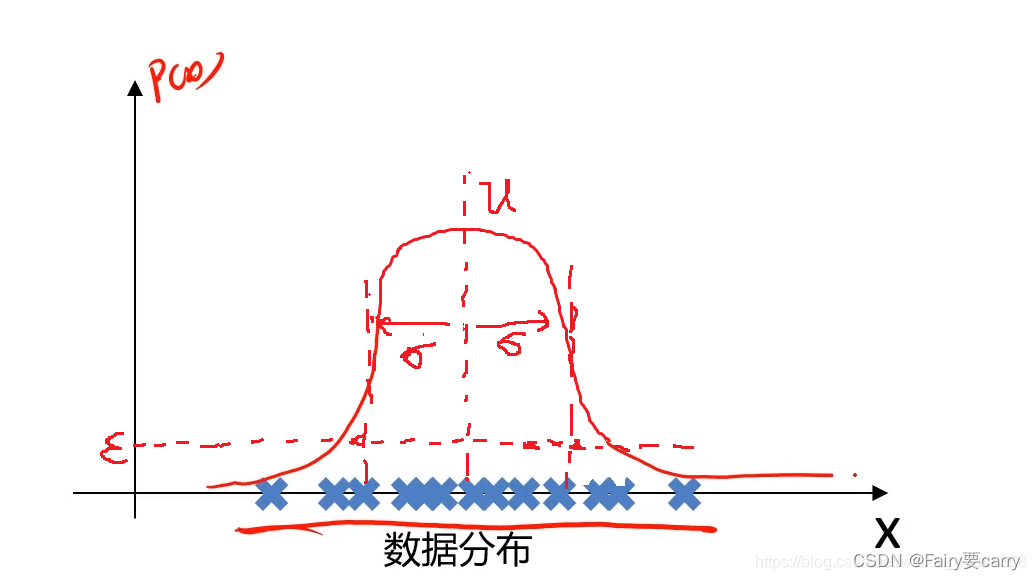
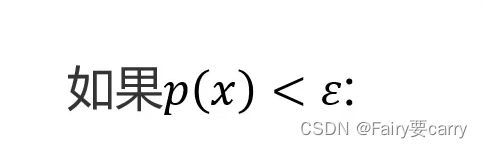该点就为异常点
问：如果数据高于一维怎么办？
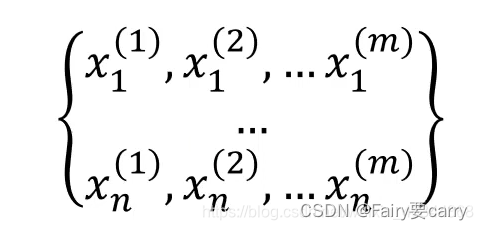
比如这里n维的数据，每一个维度都有m个样本。若要计算其高斯分布概率密度函数，可按如下步骤:
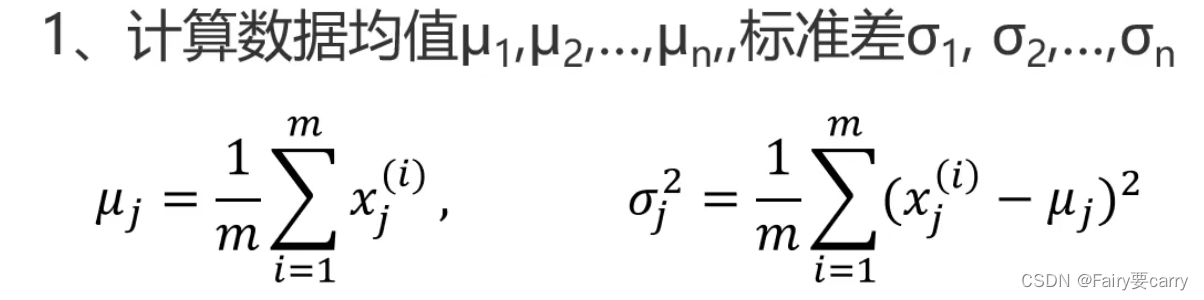先计算出每一个维度下对应的均值和标准差了，这样就可以计算每个维度下的概率密度函数
我们将计算出的每个维度下的概率密度函数相乘就可以计算出总的概率密度函数了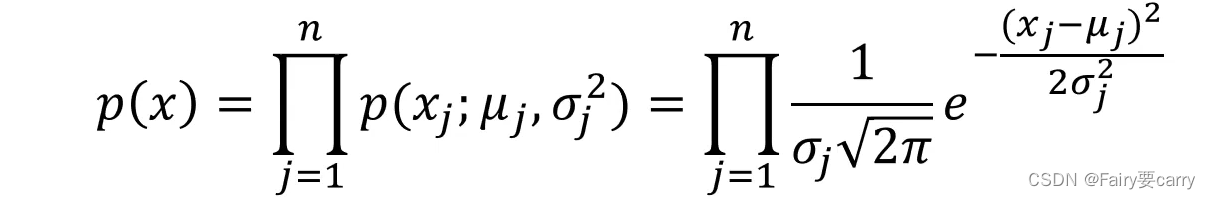
最后再根据高维下的概率密度函数判断其是否小于预期就可以判断异常点了
5.举个例子：
举个例子，下面给出一组二维数据，来判断当x1=3.5,x2=3.5时，对应的点是不是异常点
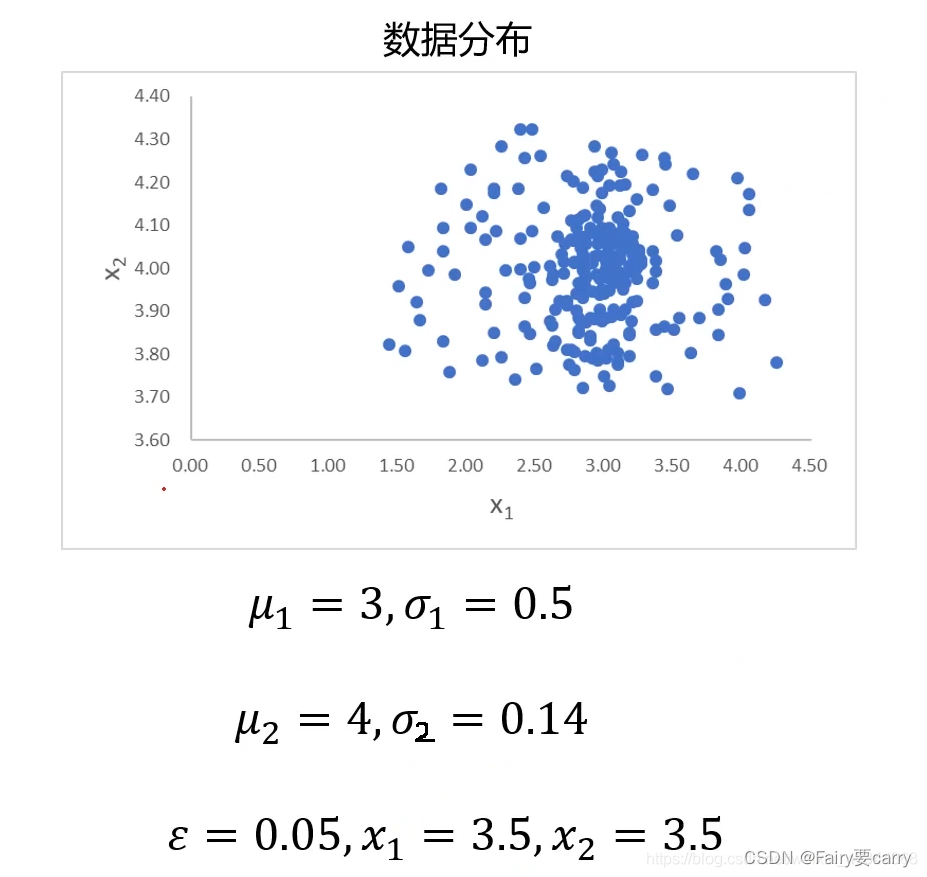
知道了标准差和均值，就可以计算其概率密度函数了
经计算可判断该点为异常点
很多时候，为了更直观的观察概率密度函数，我们是可以把它画出来的，下图是二维数据下的一个概率密度函数图
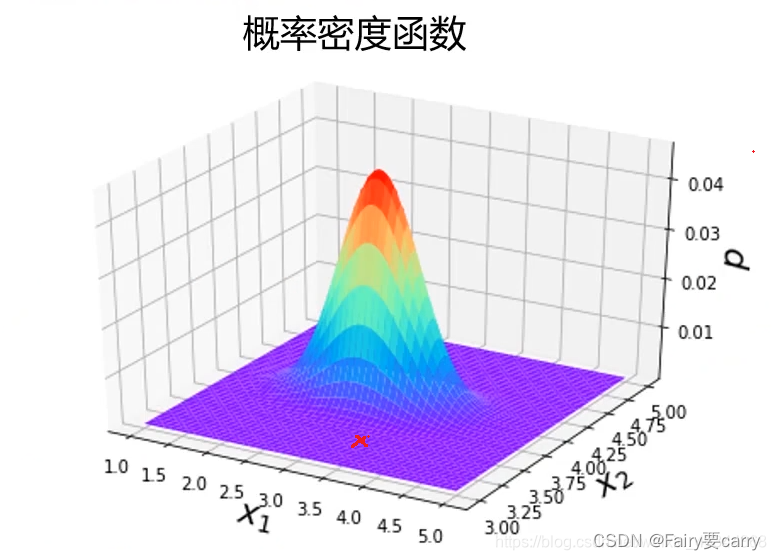
6.实战代码：
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import matplotlib as mlp # mlp设置字体
from scipy.stats import norm # norm计算高斯分布概率函数
from sklearn.covariance import EllipticEnvelope # EllipticEnvelope模型专门做异常检测的
# 1.预览数据
data = pd.read_csv('D:/pythonDATA/anomaly_data.csv')
print(data.head())
# 2.进行数据分布可视化
fig1 = plt.figure(figsize=(10, 7))
x1 = data.loc[:, 'x1']
x2 = data.loc[:, 'x2']
font2 = {'family': 'SimHei', 'weight': 'normal', 'size': '20'} # 定义一下字体（根据自己喜好定义即可）
mlp.rcParams['font.family'] = 'SimHei' # 设置字体
mlp.rcParams['axes.unicode_minus'] = False # 字符显示
fig2 = plt.figure(figsize=(20, 7))
plt.subplot(121) # 子图一行二列所属第一列（画x1）
plt.hist(x1, bins=100) # 分成100个数据分隔，即有100条条状图
plt.title('x1 数据分布统计', font2)
plt.xlabel('x1', font2)
plt.ylabel('出现次数', font2)
plt.subplot(122) # 子图一行二列所属第二列（画x2）
plt.hist(x2, bins=100) # 分成100个数据分隔
plt.title('x2 数据分布统计', font2)
plt.xlabel('x2', font2)
plt.ylabel('出现次数', font2)
plt.show()
# 3.计算x1、x2的均值(mean)和标准差(sigma)
print("计算x1，x2的mean均值和标准差sigma")
x1_mean = x1.mean()
x1_sigma = x1.std()
x2_mean = x2.mean()
x2_sigma = x2.std()
print(x1_mean, x1_sigma, x2_mean, x2_sigma)
# 4.计算高斯分布概率密度函数
x1_range = np.linspace(0, 20, 300) # x1值得范围是0到20，300个点均分
x1_normal = norm.pdf(x1_range, x1_mean, x1_sigma) # 计算高斯分布概率密度函数x_normal
x2_range = np.linspace(0, 20, 300)
x2_normal = norm.pdf(x2_range, x2_mean, x2_sigma)
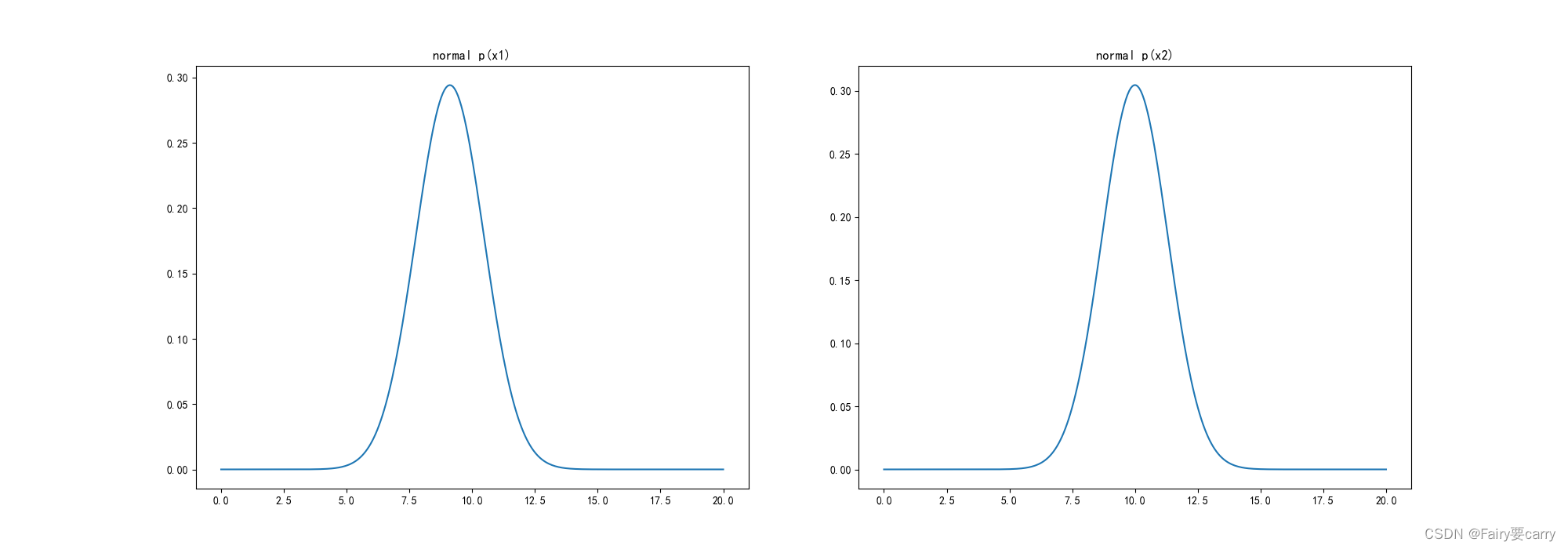
# 5.可视化高斯分布概率密度函数
fig3 = plt.figure(figsize=(20, 7))
plt.subplot(121)
plt.plot(x1_range, x1_normal) # 可视化分布概率函数(x1的值切分做x，高斯分布概率函数作y)
plt.title('normal p(x1)')
plt.subplot(122)
plt.plot(x2_range, x2_normal) # 可视化分布概率函数(x2的值切分作为x轴，y轴为高斯分布概率函数)
plt.title('normal p(x2)')
plt.show()
# 6.建立模型
ad_model = EllipticEnvelope(contamination=0.03) # 默认阈值是0.1，我们修改为0.03观察变化
ad_model.fit(data)
# 7.预测
y_predict = ad_model.predict(data)
print(pd.value_counts(y_predict))
y_predict = np.array(y_predict)
# 可视化结果
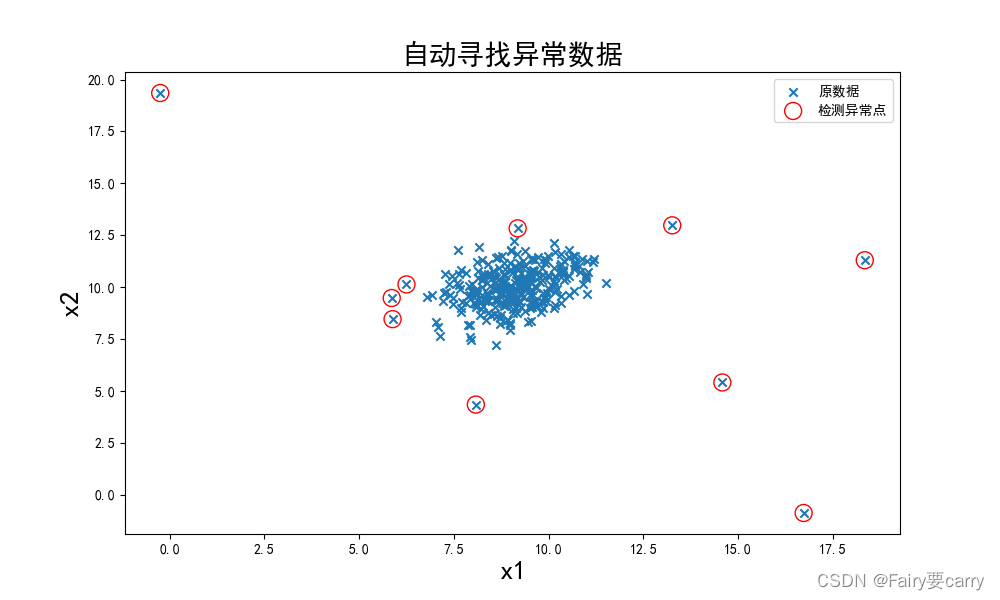
fig4 = plt.figure(figsize=(10, 6))
orginal_data = plt.scatter(data.loc[:, 'x1'], data.loc[:, 'x2'], marker='x') # 将各点用'x'表示
anomaly_data = plt.scatter(data.loc[:, 'x1'][y_predict == -1], data.loc[:, 'x2'][y_predict == -1], marker='o',
facecolor='none', edgecolor='red', s=150)
# y_predict==-1即是异常点; marker='o'将异常点用圆圈圈起来; facecolor='none' 不填充，即空心圆; edgecolor='red' 颜色为红色; s=150 圆圈的大小.
plt.title('自动寻找异常数据', font2)
plt.xlabel('x1', font2)
plt.ylabel('x2', font2)
plt.legend((orginal_data, anomaly_data), ('原数据', '检测异常点'))
plt.show()
数据分布图：
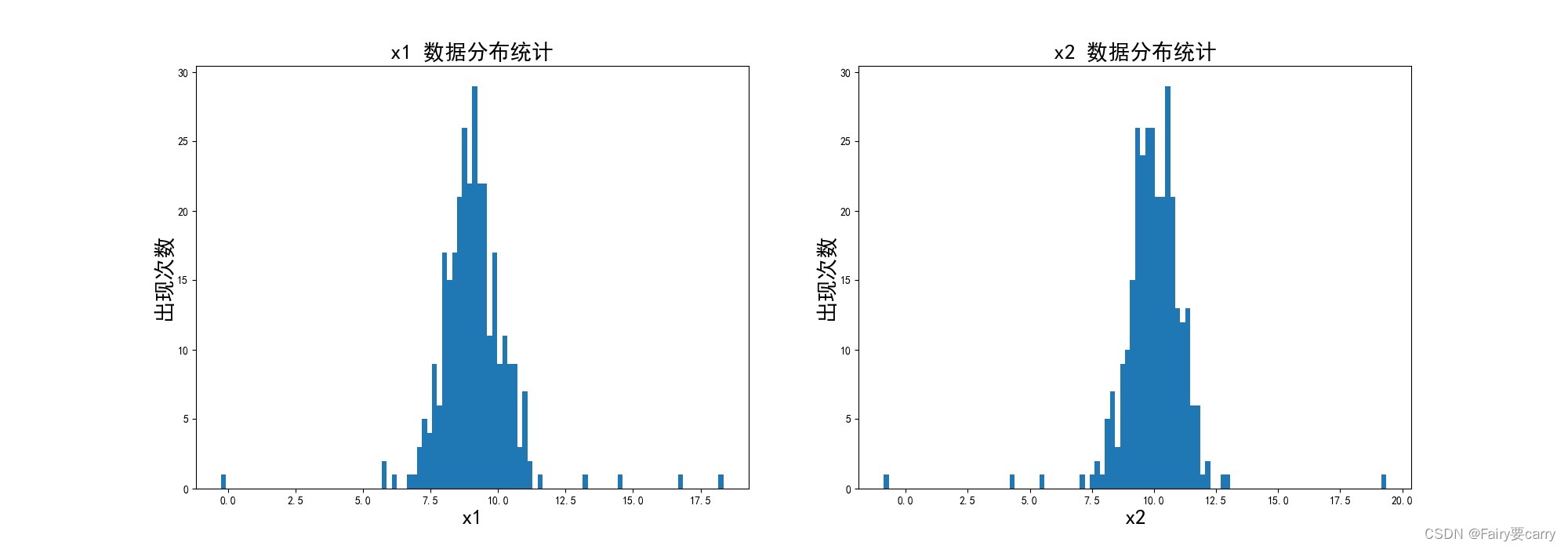
高斯概率分布图：
异常数据分布图：
