C++笔试强训day20

news2024/11/23 21:54:07

1.经此一役小红所向无敌

2.连续子数组最大和

3.非对称之美

1.经此一役小红所向无敌

链接

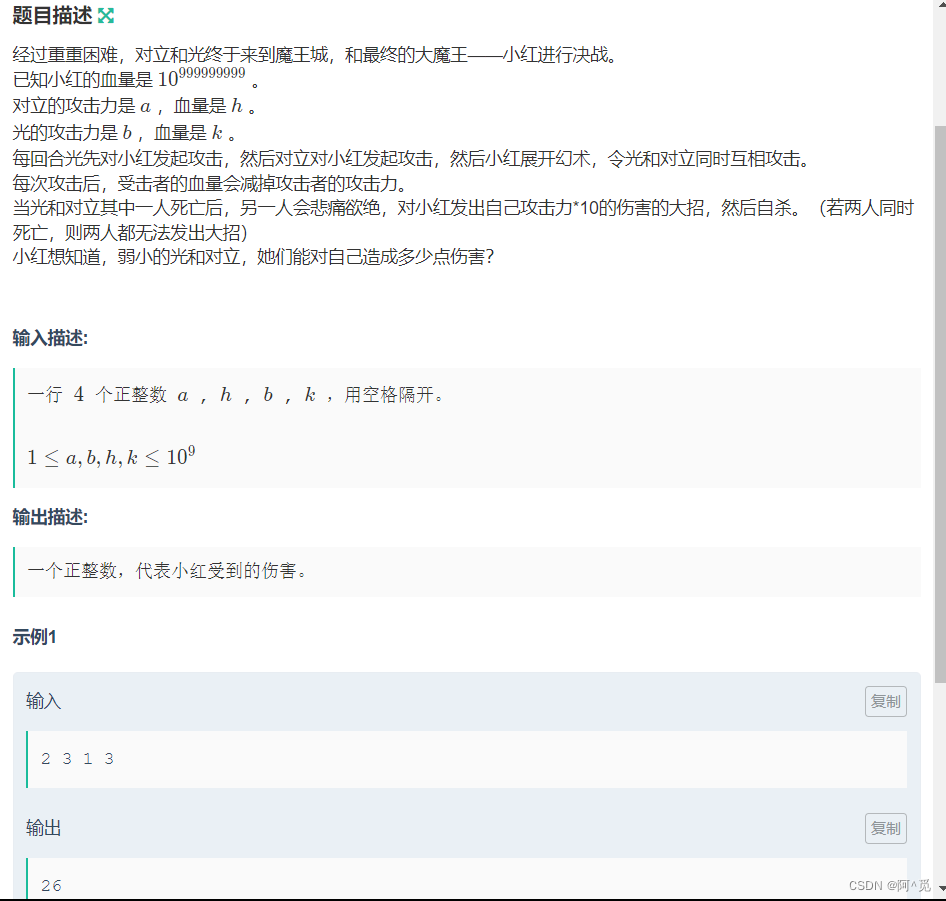
简单模拟即可。

需要注意的是：

除完之后有无余数，若有，则还可以再挨一次打。

#include <iostream>
using namespace std;
#define int long long
int a, h, b, k;
signed main() {
	cin >> a >> h >> b >> k;
    
	int sum = 0;
	int cnt1 = h / b;
	int cnt2 = k / a;
	if (h % b != 0)
		cnt1++;
	if (k % a != 0)
		cnt2++;
    
	int cnt = min(cnt1, cnt2);
	sum += cnt * (a + b);
    
	if (cnt1 == cnt2)
		cout << sum << endl;
	else if (cnt1 > cnt2)
	{
		sum += a * 10;
		cout << sum << endl;
	}
	else if (cnt1 < cnt2)
	{
		sum += b * 10;
		cout << sum << endl;
	}
	return 0;
}

2.连续子数组最大和

链接

一道线性dp问题，最主要的是找出dp所表示的含义：

dp[i], 以i为结尾，可以表示的最大数值。

#include <iostream>
using namespace std;

const int N = 2e5 + 10;
int dp[N];
int v[N];
int main() {
    int n;
    cin >> n;

    for(int i = 1; i <= n; ++i)
        cin >> v[i]; 

    for(int i = 1; i <= n; ++i)
        dp[i] = max(dp[i - 1] + v[i], v[i]);

    int ret = -101;
    for(int i = 1; i <= n; ++i)
        ret = max(dp[i], ret);

    cout << ret << endl;
    return 0;
}

填完表后，遍历一遍表中的数，取出最大值即可。

由于，因此可以让 ret 初始化为 -101。

3.非对称之美

链接

我认为这就是一道数学分析找规律题，暴力强解复杂度太高，易超时，解不出来。

但是这个规律也不好找：

#include <iostream>
#include <string>
using namespace std;
int n;
string s;
int fun()
{
	// 1. 判断是否全都是相同字符
	bool flag = false;
	for (int i = 1; i < n; i++)
	{
		if (s[i] != s[0])
		{
			flag = true;
			break;
		}
	}
	if (flag == false) 
        return 0;
	// 2. 判断本⾝是否是回⽂
	flag = true;
	int left = 0, right = n - 1;
	while (left < right)
	{
		if (s[left] == s[right])
		{
			left++;
			right--;
		}
		else
		{
			flag = false;
			break;
		}
	}

	if (flag) 
        return n - 1;
	else 
        return n;
}
int main()
{
	cin >> s;
	n = s.size();

	cout << fun() << endl;

	return 0;
}