1. 图(节点+边)

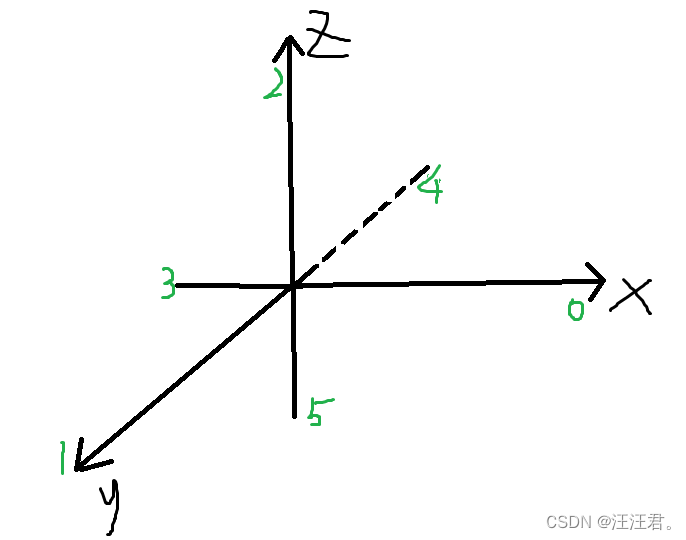
一个图可以由节点和边组成，假设我们有一个节点notes ：n=4,边edges：m=5的有向图，表示如下

• 通过以上电路图可以得到关联矩阵(incident matrix),我们定义边，开始端用-1表示，结束端用1表示，用行表示边，用列表示节点。可得如下
  比如edge1是由从节点1出发，到节点2 ，用行向量表示可得
  $$\left[\begin{array}{cccc}-1& 1& 0& 0\end{array}\right]\Rightarrow edge1\text{\hspace{1em}(1)}$$
• 所以矩阵A根据上图可得如下：
  $$A=\left[\begin{array}{cccc}-1& 1& 0& 0\\ & & & \\ 0& -1& 1& 0\\ & & & \\ -1& 0& 1& 0\\ & & & \\ -1& 0& 0& 1\\ & & & \\ 0& 0& -1& 1\end{array}\right]\text{\hspace{1em}(2)}$$

  • 我们可以看到由边1，2，3组成一个子图，那么看看由1，2，3组成的矩阵表示如下：
    $$\left[\begin{array}{cccc}-1& 1& 0& 0\\ & & & \\ 0& -1& 1& 0\\ & & & \\ -1& 0& 1& 0\end{array}\right]\Rightarrow ro{w}_1+ro{w}_2=ro{w}_3\text{\hspace{1em}(2)}$$
    

    也就是说，如果在矩阵中3行能达到等式关系，可以等效与在图上形成一个子图。

    • 那么矩阵A的零空间代表什么呢？我们将AX=0 用列的形式表示如下：
      $$AX=\left[\begin{array}{cccc}-1& 1& 0& 0\\ & & & \\ 0& -1& 1& 0\\ & & & \\ -1& 0& 1& 0\\ & & & \\ -1& 0& 0& 1\\ & & & \\ 0& 0& -1& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ \\ x_2\\ \\ x_3\\ \\ x_4\end{array}\right]=\left[\begin{array}{c}{x}_2-x_1\\ \\ x_3-x_2\\ \\ x_3-x_1\\ \\ x_4-x_3\end{array}\right]\text{\hspace{1em}(2)}$$
      $$AX=\left[\begin{array}{c}-1\\ \\ 0\\ \\ -1\\ \\ -1\\ \\ 0\end{array}\right]x_1+\left[\begin{array}{c}1\\ \\ -1\\ \\ 0\\ \\ 0\\ \\ 0\end{array}\right]x_2+\left[\begin{array}{c}0\\ \\ 1\\ \\ 1\\ \\ 0\\ \\ -1\end{array}\right]x_3+\left[\begin{array}{c}0\\ \\ 0\\ \\ 0\\ \\ 1\\ \\ 1\end{array}\right]x_4\text{\hspace{1em}(3)}$$
• AX=0的零空间X表示的是列向量的线性组合。X的物理意义表示的每个节点的电势值[potential at the node ]，那么$x_2-x_1$表示的是edge1的电势差，那什么时候可以保证电势差为0呢，那只有每个结点的电势相同即可，所以可以得到解如下，所以 dim $N(A)=1$
  $$X=c\left[\begin{array}{c}1\\ \\ 1\\ \\ 1\\ \\ 1\end{array}\right]\text{\hspace{1em}(4)}$$