题目

困难

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

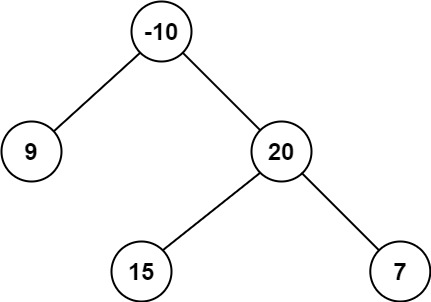
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

---

面试中遇到过这道题?

1/5

是

否

通过次数

410.4K

提交次数

901.1K

通过率

45.5%

思路

按照题目对路径的定义，一个结点可以连接他的左子树结点和他的右子树结点。

若左子树的路径大于0，则说明左子树的路径对根节点的路径和有增大的帮助，这是可以加上左子树的路径和。

对于右子树，也是一样的。

左右子树对路径和的帮助加上根节点的值就是以该节点为根的数的最大路径和。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxsum=-1000000000;
    int maxpath(TreeNode* root)
    {
        if(!root) return 0;
        //左右子树的最大贡献，大于零才有贡献
        int leftmax=max(maxpath(root->left),0);
        int rightmax=max(maxpath(root->right),0);
        maxsum=max(maxsum,(leftmax+rightmax+root->val));
        //该节点的最大贡献
        return root->val+max(leftmax,rightmax);
    }
    int maxPathSum(TreeNode* root) {
        maxpath(root);
        return maxsum;
    }
};