系列文章目录

---

前言

本人最近再练习算法，所以会发布一些解题思路，希望大家多指教

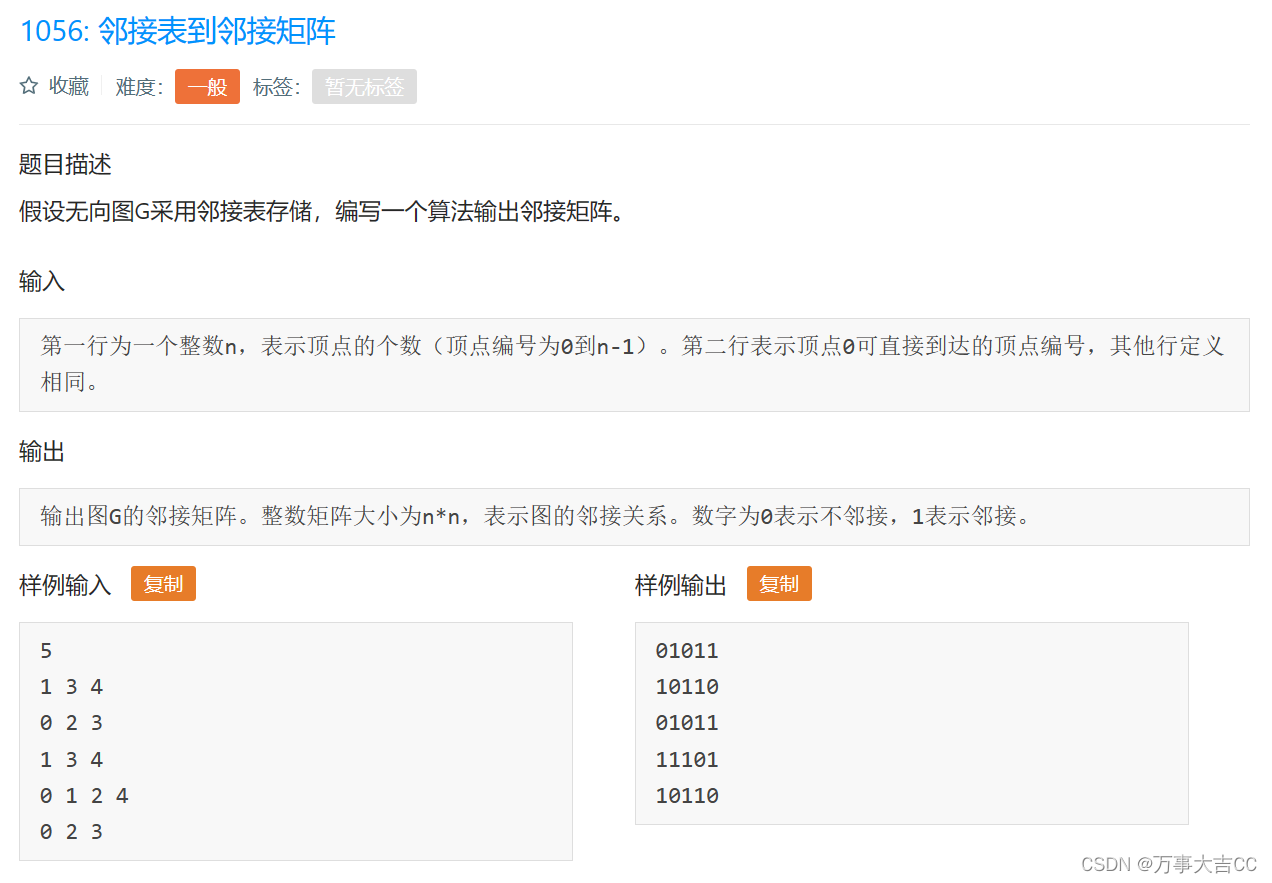
一、题目描述

如果矩阵中的许多系数都为零，那么该矩阵就是稀疏的。对稀疏现象有兴趣是因为它的开发可以带来巨大的计算节省，并且在许多大的实践中都会出现矩阵稀疏的问题。

给定一个矩阵，现在需要逐行和逐列地扫描矩阵，如果某一行或者某一列内，存在连续出现的0的个数超过了行宽或者列宽的一半，则认为该行或者该列是稀疏的。

二、输入描述

第一行输入两个数，分别为M和N

接下来M行输入为矩阵的成员，每行N个成员，矩阵成员都是整数，范围-32768~32767

三、输出描述

输出两行，第一行表示稀疏行的个数，第二行表示稀疏列的个数。

四、Java代码

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        // 行的数量
        int M = sc.nextInt();
        // 列的数量
        int N = sc.nextInt();
        // 正矩阵（行是行，列是列）
        int[][] rowArr = new int[M][N];
        //通过二维数组接受矩阵信息
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                rowArr[i][j] = sc.nextInt();
            }
        }
        //初始化满足稀疏行的行数
        int rowTimes = 0;
        //初始化每行最大连续0的个数
        int maxRowCount = 0;
        //初始化每行连续0的个数
        int rowCount = 1;

        //初始化每列连续0的个数
        int colCount = 0;
        //初始化满足稀疏列的列数
        int colTimes = 0;
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                //处理行数据
                if(rowArr[i][j] == 0){
                    if(j+1 < N && rowArr[i][j+1] == 0){
                        rowCount++;
                    }
                } else {
                    //行遍历过程中遇到1时，以为连续的0被断开，需要比较得出当前连续0的最大长度，及将rowCount重置为1
                    maxRowCount = Math.max(rowCount, maxRowCount);
                    rowCount = 1;
                }
                //列的处理，只需要在遍历第一行数据时，通过深度搜索进行判断
                if(i == 0){
                    //处理列
                    maxColcount = dfs(rowArr, i, j, M, colCount);
                    if(maxColcount > M/2){
                        colTimes++;
                    }
                    //每列遍历结束后，将maxColcount重置为0
                    maxColcount = 0;
                }
            }
            if(maxRowCount > N/2){
                rowTimes++;
            }
            //每行遍历结束后，将maxCount重置为0
            maxRowCount = 0;
        }

        System.out.println("稀疏行的个数："+rowTimes);
        System.out.println("稀疏列的个数："+colTimes);
    }

    //初始化每列最大连续0的个数
    static int maxColcount = 0;
    private static int dfs(int[][] rowArr, int i, int j, int m, int colCount) {
        if(rowArr[i][j] == 0){
            colCount++;
        }
        int x = i+1;
        if(x>=0 && x < m){
            if(rowArr[x][j] == 1){
                //当前元素为1，则需要断开连续区间，求出当前最大的连续0长度，重置colCount
                maxColcount = Math.max(maxColcount, colCount);
                colCount = 0;
            }
            //继续向下深度搜索
            colCount = dfs(rowArr, x, j, m, colCount);
        }
        return Math.max(maxColcount, colCount);
    }

五、测试用例

输入：
7 6
1 1 0 1 1 0
0 1 0 0 0 1
1 0 0 0 1 0
1 0 0 0 0 0
0 1 1 0 0 0
1 0 0 0 0 1
1 0 0 0 0 1
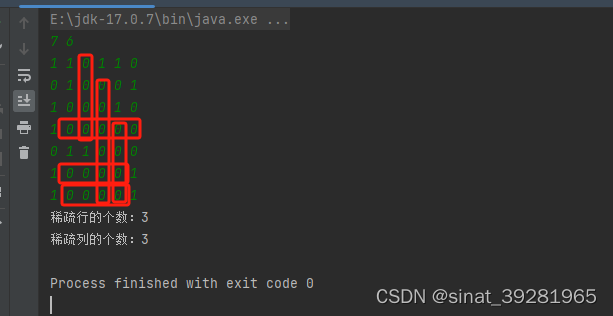
输出：

提示

也可以通过，矩阵反转来处理列的数据，本人有点偷懒，所以就直接在处理第一行元素的时候，顺便处理了列的数据。