题目一：如何仅用递归函数和栈操作逆序一个栈

      题目要求：

    一个栈依次压入 1、2、3、4、5，那么从栈顶到栈底分别为5、4、3、2、1。将这个栈
转置后，从栈顶到栈底为 1、2、3、4、5，也就是实现栈中元素的逆序，但是只能用递归函数来实现，不能用其他数据结构。

      题目解析：

   根据题目要求，我们需要使用递归函数，依次将栈中的元素进行逆置出来。我们可以根据递归函数所可能产生的影响进行问题的解决。

   由于递归函数在递归的结束的时候可以进行返回，所以我们如果拿到一个数据并删除的话，在最后返回的时候会拿到最后一个数据。所进行的操作如下：

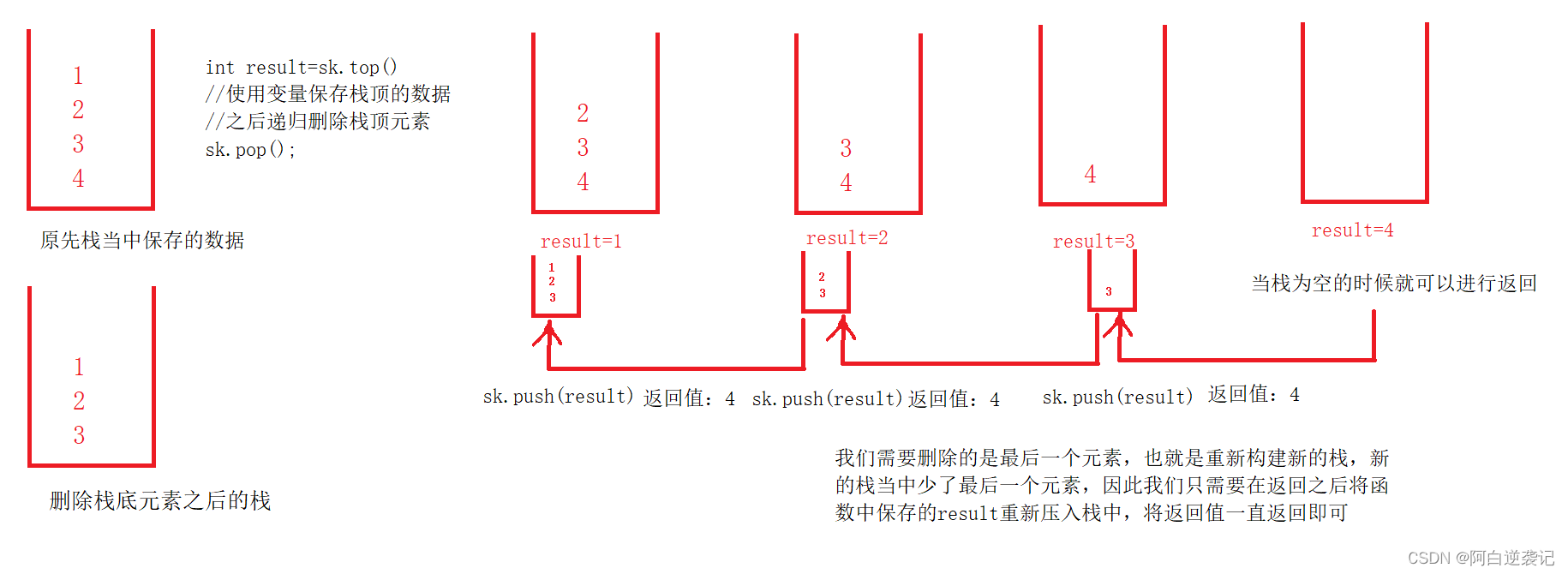
  如果想要将数组进行逆序仅仅拿到最后一个数据是完全不够的，我们还需要思考如何将一个数组进行逆序，这个思路其实很简单。我们可以再次使用一次递归操作，每次拿出最下面的数据，并保存，之后我们递归返回的时候就可以拿到最上面的数据了。我们将数据依次压入栈中就会得到一个逆序的栈。

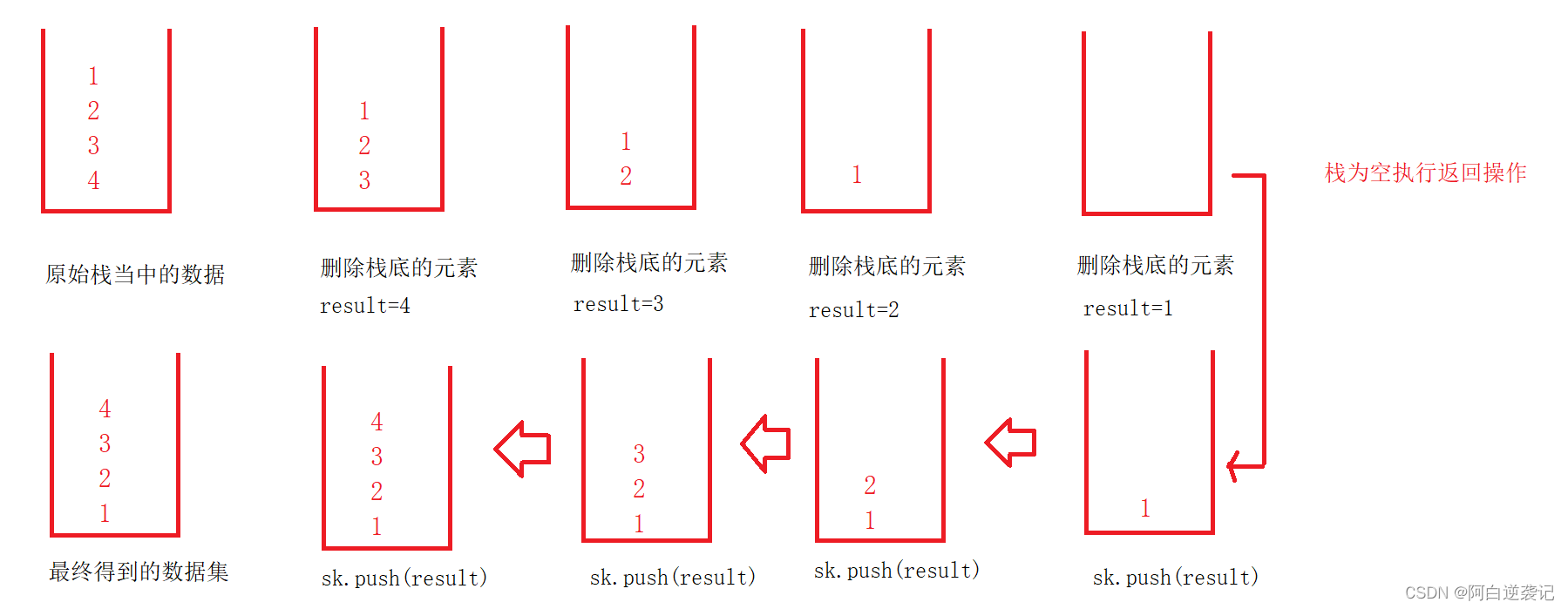
    根据上述思路我们可以设计两个递归函数实现栈的逆序操作，实现代码如下：

#include<iostream>
#include<stack>
using namespace std;

int getAndRemoveLastElem(stack<int>& sk)
{
	int result = sk.top();
	sk.pop();
	if (sk.empty())
	{
		return result;
	}
	else
	{
		//继续进行递归删除操作
		int last = getAndRemoveLastElem(sk);
		sk.push(result);
		return last;
	}
}

//最后通过调用递归函数
void StackReverseStack(stack<int>& sk)
{
	if (sk.empty())
	{
		return;
	}
	int i = getAndRemoveLastElem(sk);
	StackReverseStack(sk);
	sk.push(i);
}

int main()
{
	stack<int> ret;
	ret.push(1);
	ret.push(2);
	ret.push(3);
	ret.push(4);
	ret.push(5);
	StackReverseStack(ret);
	//之后打印输出栈当中的内容检查逆序的状况
	while (!ret.empty())
	{
		cout << ret.top() << endl;
		ret.pop();
	}

	return 0;
}

        题目二：用栈来求解汉诺塔问题

      题目要求： 
   汉诺塔问题比较经典，这里修改一下游戏规则：现在限制不能从最左侧的塔直接移动
到最右侧，也不能从最右侧直接移动到最左侧，而是必须经过中间。求当塔有 N层的时候,需要最少移动多少步。

    题目解析：

    这道题我们可以将其认为是一个简单的模拟类的题目，首先我们来分析问题：

    题目当中要求我们所进行的移动的步数是最少的，因此不允许由连续的可逆的步骤存在。例如：上一步从左到中间进行移动，下一步就从中间到左进行移动。这样上一步移动的步骤就是完全没有效果的，不可能是最少的移动次数。

   其次，题目当中要求我们在移动的时候必须经过中间，因此我们可以判断，当两个柱子进行移动完成之后（其中一个柱子一定是中间的柱子）一定是中间的柱子和另外一个没有进行移动的柱子进行移动操作，无非就是从中间移动到目标位置，或者从目标位置移动到中间。我们只需要符合汉诺塔的规则即可，也就是小的数据必须在大的数据之上才可以进行移动。所进行的示例如下：

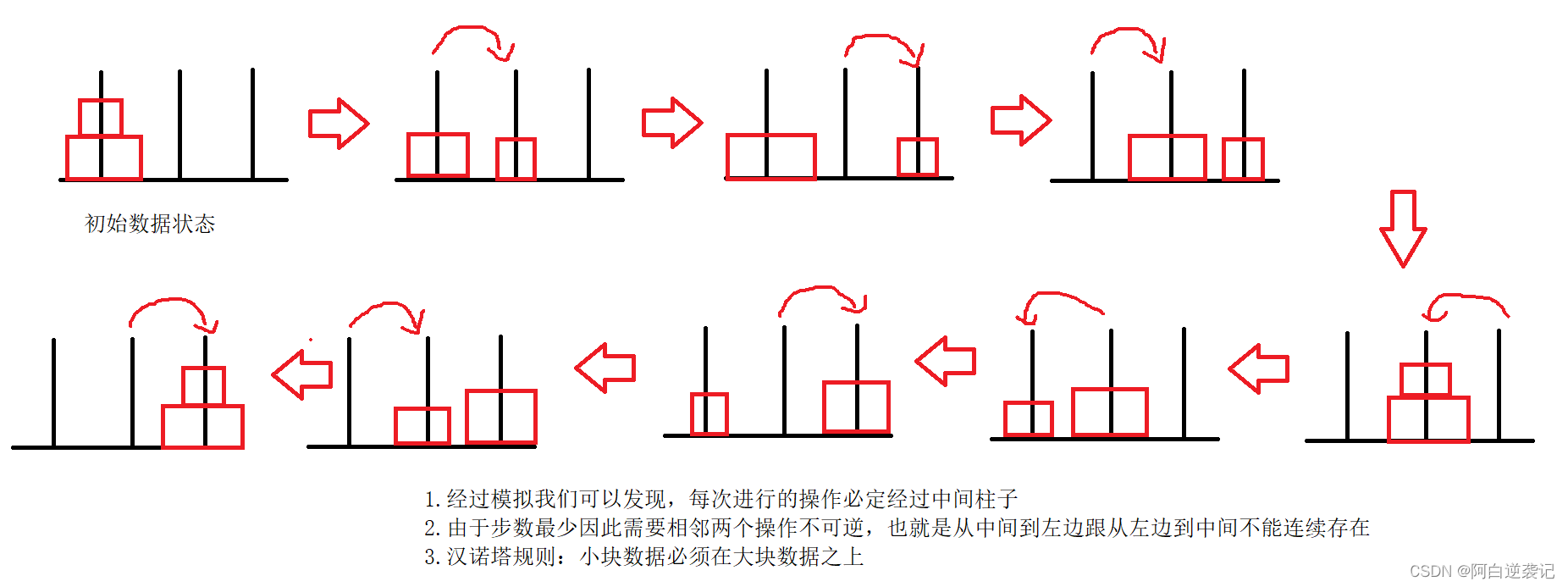
    我们可以设置两个变量用于作为记录两个变化的柱子的情况，之后排除中间的柱子，让另一根柱子跟中间柱子进行数据的移动即可。根据上述思路我们可以写出如下代码：

#include<iostream>
#include<stack>
#include<vector>
#include<string>
using namespace std;
//使用栈进行解决汉诺塔问题
int stackSloveHanio(int data)
{
	stack<int> left;
	while (data)
	{
		left.push(data);
		data--;
	}
	stack<int> mid;
	stack<int> right;
	//经过第一次初始化之后进行统一的数据操作
	int from = 1;
	int to = 2;     //使用1，2，3表示左中右三个柱子
	int x = left.top();
	left.pop();
	mid.push(x);
	int count = 1;
	//之后检查三个柱子的情况得到最终想要的结果
	while (!left.empty() || !mid.empty())
	{
		//当左边跟中间的柱子都不为空的时候就继续循环查找新的初始情况
		//由判断可知，我们的from和to无论怎么移动一定与中间柱子有关，
		//因此我们只需要查找中间柱子跟另外一个没有用到的柱子的移动方向即可
		int tmp = from;
		if (from == 2)
		{
			tmp = to;
		}
		if (tmp == 1)  //下一次进行的操作就需要是从另外一个柱子跟中间柱子移动数据
		{
			//判断3柱子移动到中间，还是从中间移动到3柱子
			if (!right.empty()&&(mid.empty() || right.top() < mid.top()))
			{
				//从3移动到2
				mid.push(right.top());
				right.pop();
				from = 3;
				to = 2;
			}
			else
			{
				//从2移动到3
				right.push(mid.top());
				mid.pop();
				from = 2;
				to = 3;
			}
			count++;
		}
		if (tmp == 3)
		{
			//同理可得
			if (!left.empty()&&(mid.empty() || left.top() < mid.top()))
			{
				mid.push(left.top());
				left.pop();
				from = 1;
				to = 2;
			}
			else
			{
				left.push(mid.top());
				mid.pop();
				from = 2;
				to = 1;
			}
			count++;
		}
	}
	return count;
}
int main()
{
	cout<<stackSloveHanio(3);
	return 0;
}

        题目三：生成窗口最大值数组

      题目要求：
  有一个整型数组 arr 和一个大小为 w 的窗口从数组的最左边滑到最右边，窗口每次向
右边滑一个位置。
例如，数组为[4,3,5,4.3,3,6,7]，窗口大小为 3 时:
[4 3 5] 4 3 3 6 7          窗口中最大值为 5
4 [3 5 4] 3 3 6 7          窗口中最大值为 5
4 3 [5 4 3] 3 6 7          窗口中最大值为 5
4 3 5 14 3 3] 6 7         窗口中最大值为 4
4 3 5 4 [3 3 6] 7          窗口中最大值为 6
4 3 5 4 3 [3 6 7]          窗口中最大值为 7
如果数组长度为 n，窗口大小为 w，则一共产生 n-w+1 个窗口的最大值。

请实现一个函数。
•输入：整型数组 arr，窗口大小为 w.
•输出：一个长度为 n-W+1 的数组 res，res[i]表示每一种窗口状态下的最大值。
以本题为例，结果应该返回{5,5,5,4,6,7}。

     题目解析：

   这道题目实际上想要让我们进行的操作也就是根据指定的窗口依次选出窗口内元素的最大值。拿到这道题目的时候我们首先会有一个思路：直接进行模拟不久行了嘛，每次有新的数据进入窗口的时候进行一次遍历，得到最大的值，加入到数组当中。但是我们来思考一下时间复杂度：每一次遍历窗口一遍，假设窗口的大小为M，数据总共N个，所以我们总的时间复杂度为O（MN）这并不是一个很好的算法，因此我们需要进行优化。

  书中有一个很奇妙的思想：试想一下，在我们的窗口当中有新加入的元素，当新加入的元素较大的时候前面较小的元素就不可能是最大的元素，我们可以直接前面较小的数据删除。当新加入的数据较小的时候，当前面较大的数据删除之后，那么这个暂时较小的数据就有可能是最大的了。所以我们需要将数据保存。

  借助双端队列进行优化我们的代码。我们可以进行一次数组遍历，当队列为空或者新数据小于队列尾部的数据的时候可以直接将数据的下标加入到队列的尾部，当新数据大于队列尾部的数据的时候，直接将队列尾部的数据进行弹出数据。知道队列当中的数据大于新数据或者队列为空为止。所要进行的操作如下：

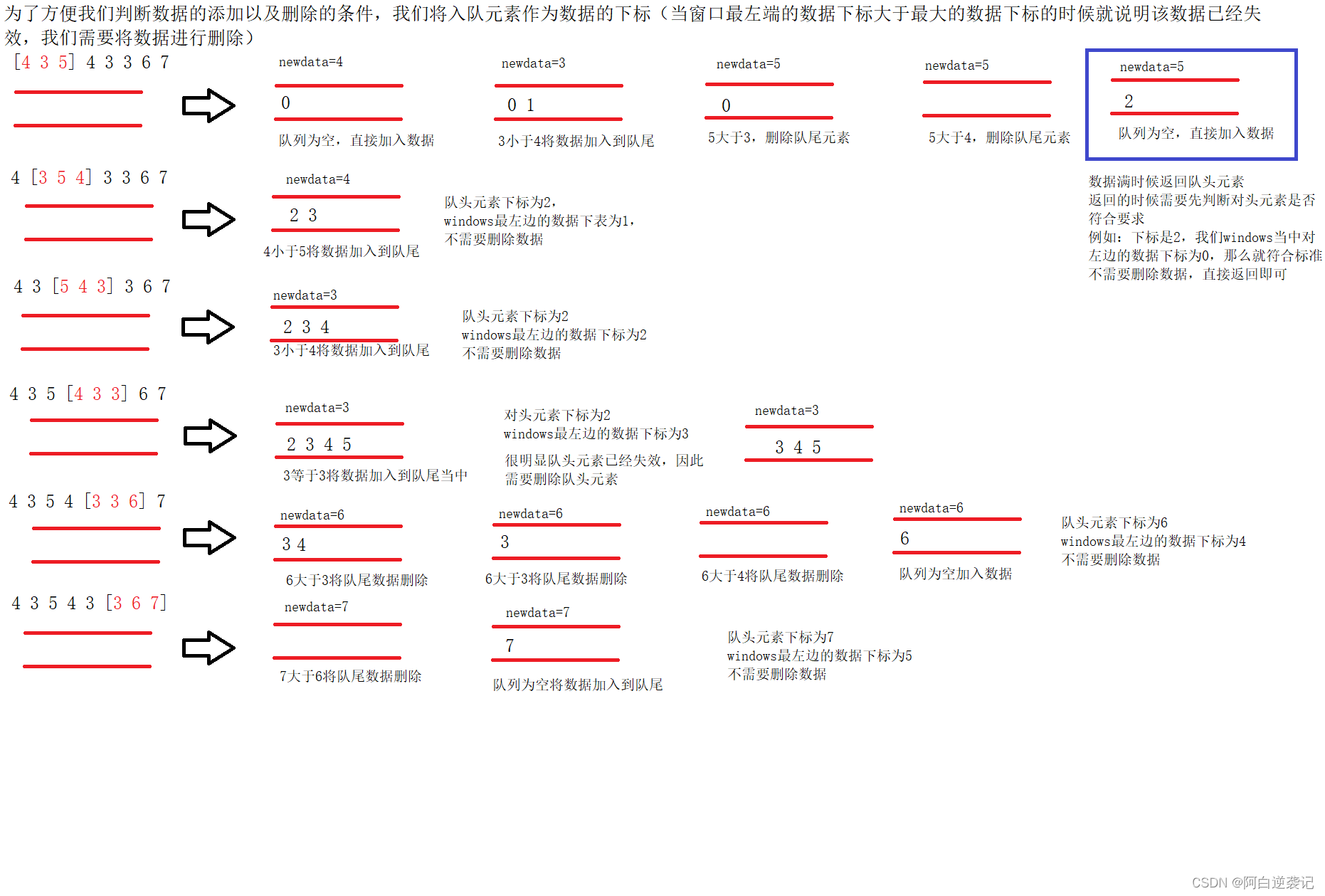
    需要注意的是：由于为了方便我们判断数据的加入以及输出的边界条件，因此我们需要将数组的下标作为加入队列的元素。当我们的队头元素小于我们窗口最左侧元素的下标的时候就说明数据已经失效，需要将队头数据删除，获得下一个窗口当中最大的元素。根据上述思路我们可以编写出如下的代码：

#include<iostream>
#include<vector>
#include<queue>
using namespace std;

//编写一个函数，用于查找生成窗口最大值的数组
vector<int> createMaxWindow(vector<int> ret, int windows)
{
	//我们需要借助一个栈进行解决这个问题
	deque<int> dq;
	vector<int> finEnd;
	int count = windows;
	//进行数据的遍历操作，将我们数组当中的内容的下标依次放到栈当中，如果之后进入的数据大于之前的数据
	//就直接进行入栈操作，否则需要先执行出栈操作，等到满足小于之前的元素的时候就可以执行入栈操作了
	for (int i=0;i<ret.size();i++)
	{
		while (!dq.empty()&&ret[i]>ret[dq.front()])
		{
			dq.pop_back();
		}
		dq.push_back(i);
		//之前向栈当中插入的元素还不满，不能直接进行记录最大值
		if ( count== 1)
		{
			//进行检查并返回最大值,检查栈顶的最大值是否过期
			while (i - windows >= dq.front())
			{
				dq.pop_front();    //删除过期的最大值
			}
			//找到不过期的数据直接进行记录队头元素
			finEnd.push_back(ret[dq.front()]);
		}
		else
		{
			count--;
		}
	}
	return finEnd;
}

int main()
{
	//进行测试最大生成窗口代码
	vector<int> ret({ 1,2,3,4,5,6,7,8,9 });
	vector<int> tmp=createMaxWindow(ret, 5);
	for (auto e : tmp)
	{
		cout << e << " ";
	}
	return 0;
}