---

前言

在本篇文章中，我们将会讲到leetcode中673. 最长递增子序列的个数，我们将会用动态规划方式解决这道问题，同时掌握小demo知识。

一、题目描述

给定一个未排序的整数数组 nums ， 返回最长递增子序列的个数 。

注意 这个数列必须是 严格 递增的。

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。

题目描述很简单，这里就不再过多叙述了。
注意一点：严格递增，不可以两个数相等。

二、解题步骤

1.小demo介绍

在解决这道问题之前，我们先来介绍个小demo。
在数组中一次找出最大值出现的次数。

nums={2,2,3,4,6,3,2,4};
我们可以定义两个变量maxval,count
🌟maxval表示数组中最大值，初始化为nums[ 0 ]
 count表示最大值出现的次数，初始化为1（为我们假定第一个数为最大值）
🌟nums[ i ]==maxval,count++;
🌟nums[ i ]<maxval,无视;
🌟nums[ i ]>maxval,说明当前并不是最大值，需要更新最大值和计数，maxval=nums[ i ],count=1;

2.动态规划

1.状态表示

经验+题目要求

dp[ i ]：以i位置为结尾的所有子序列中，最长递增子序列的个数

我们先来试一下是否能够推出状态转移方程。
我都不知道以 i 为结尾的最⻓递增⼦序列的「⻓度」是多少，那怎末知道个数呢？？

所以一个状态表示解决不了问题，我们必须知道多长，才能知道个数。

len[ i ]：以i位置为结尾的所有子序列中，最长递增子序列的长度
count[ i ]：以i位置为结尾的所有子序列中，最长递增子序列的个数

2.状态转移方程

我们可以两个表一起进行填写
🌟第一种情况，自己构成一个子序列，此时len[ i ]=1,count[ i ]=1;
🌟其他情况，与前面的结合形成子序列，计算len[ i ],我们在300. 最长递增子序列博客中已经讲述过了，这里不再过多阐述。
🌟我们主要看一下count[ i ]的计算。
我们要计算count[ i ],我们需要根据len[ i ],找到最长长度。
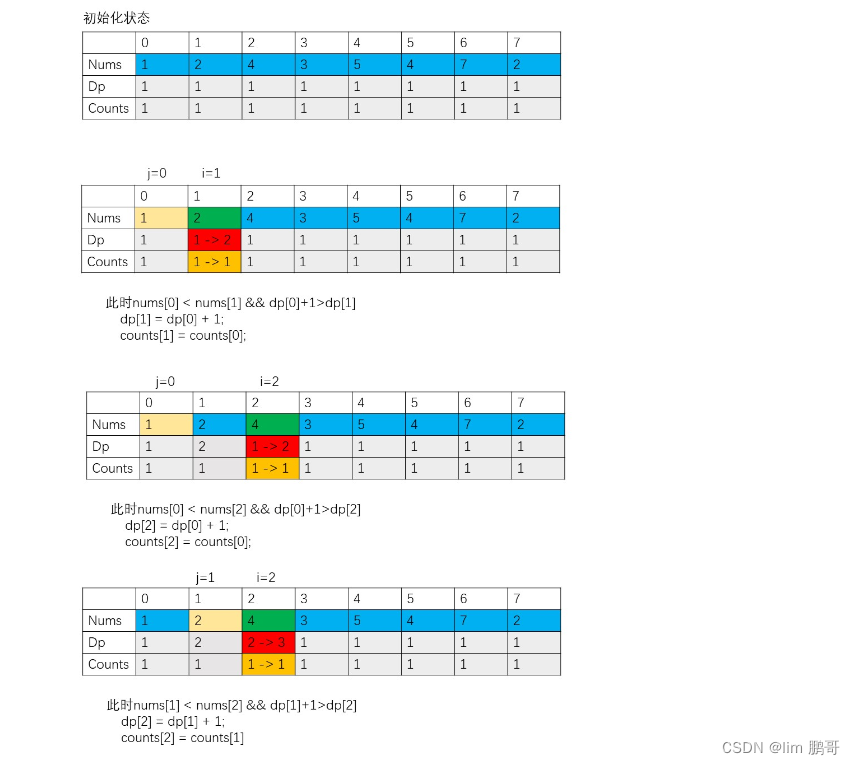
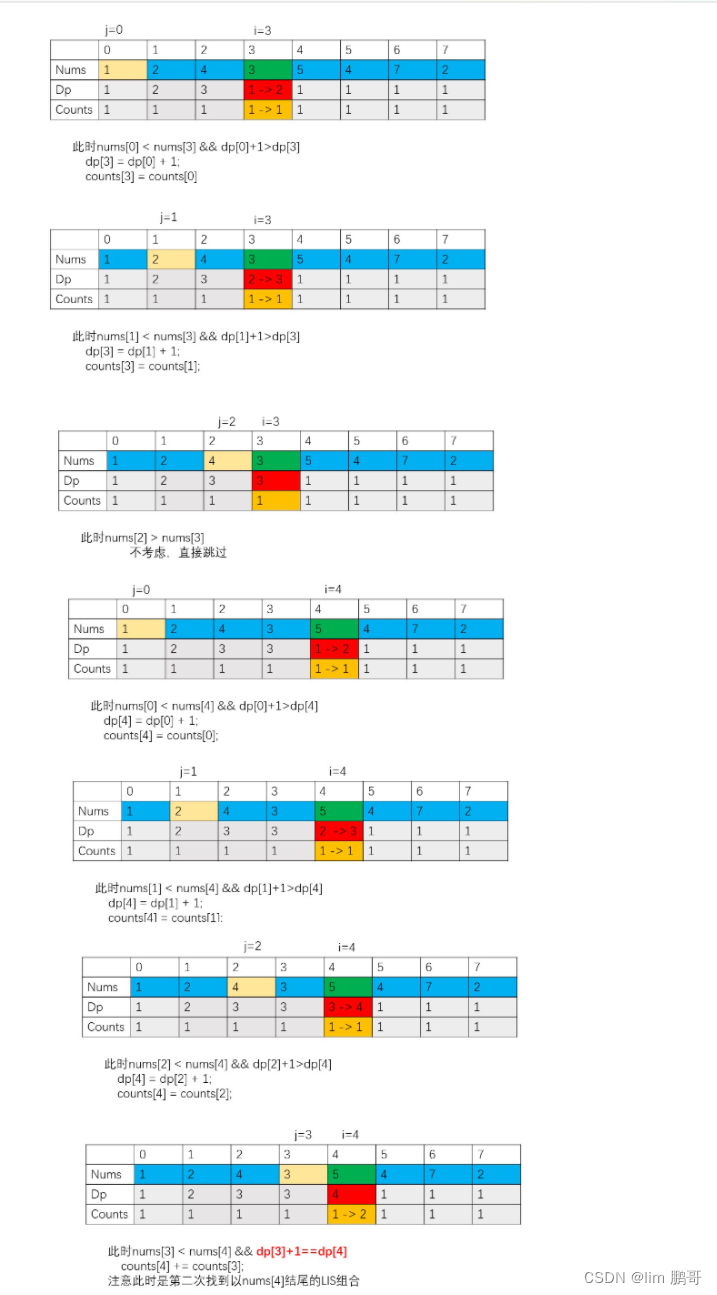
  💗💗len[ j ]+1>len[ i ].说明我们第一次找到最大长度，len[ i ]=len[ j ]+1,count[ i ]=count[ j ];
  💗💗len[ j ]+1<len[ i ],说明此时的长度还不如上次找到的长度长，可以无视
  💗💗len[ j ]+1==len[ i ],说明此时又一次找到了最大长度，count[ i ]+=count[ j ].

上面的叙述和小demo十分相似。

下面根据动图进一步理解一下

3.初始化

两个表都都初始化为1。

4.填表顺序

从左到右

5.返回值

我们用maxlen表示最长递增子序列的长度。
我们应该返回所有长度等于maxlen的子序列的个数。

这和小demo十分相似。
我们可以边填表，边进行查找。

三、代码编写

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) 
    {
        int n=nums.size();
        //创建dp表+初始化
        vector<int>len(n,1);
        vector<int>count(n,1);
        //记录最终结果
        int maxlen=1;
        int maxcount=1;
        //填表
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[j]<nums[i])
                {
                    //重新计数
                    if(len[j]+1>len[i])
                    {
                        len[i]=len[j]+1;
                        count[i]=count[j];
                    }
                    else if(len[j]+1==len[i])
                    {
                        count[i]+=count[j];
                    }
                }
            }
            if(maxlen==len[i])
            {
                maxcount+=count[i];
            }
            //重新计数
            else if(maxlen<len[i])
            {
                maxlen=len[i];
                maxcount=count[i];
            }
        }
        //返回结果
        return maxcount;
    }
};

总结

以上就是我们对Leetcode中最长递增子序列的个数详细介绍，希望对大家的学习有所帮助，仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~