A题 多源机会信号建模与导航分析
摘要
全球卫星定位系统（GPS）虽广泛应用于全球定位与导航，但其在室内、隧道以及建筑密集区等复杂环境中的有效性受限。为解决这一局限性，本研究探讨了一种基于机会信号的自主定位导航方法。
机会信号导航利用无线电信号实现飞行器的精确定位，特别是在GPS不可用的情况下。本研究首先对机会信号的五类信息（TOA, TDOA, DFD, AOA, RSSI）建立了精确的数学模型，并设计了包含简单移动平均（SMA）算法的定位系统以实现实时位置估计。
为进一步优化预测精度，引入了带有局部逃逸算子的海洋捕食者算法（MPA）。此算法模仿海洋捕食者的狩猎行为，通过动态调整搜索策略，有效逃避局部最优解，从而提高全局寻优能力。使用了包含SMA（简单移动平均）算法的实时位置估计方法。SMA算法帮助我们平滑数据，减少瞬时噪声的影响，并提高定位精度。
通过比较不同信号源的数据和实现对信号误差的深入分析，我们能够在不同接收情况下提供准确的飞行器定位。我们开发了一种机会信号的实时筛选方法来识别并排除那些具有较大偏差的信号。
对于接收情况2中存在的随机性偏差和常值飘移，我们设计了评价判断方法，并据此进行了数据调整。这一策略显著提高了信号处理的准确性，从而优化了飞行器的定位结果。我们成功地处理了随机性偏差和常值飘移，显著减少了预测误差。对比优化前后的数据显示，飞行轨迹变得更加光滑，误差进一步降低。实验结果表明，使用SMA算法和筛选方法后，飞行器的位置预测在0秒至10秒内极为准确。

关键词 SMA，LEOMPA，机会信号

问题二
不考虑数据偏差的情况我们采用混合的信息来预测飞行器导航定位结果。
发射源4的到达角度信息AOA和达到时间信息 TOA来处理。
求解结果见excel文件：‘导航定位结果.xlsx’。其中部分内容见表1
表1问题二部分结果
时间/s X坐标/m Y坐标/m Z坐标/m
0.01 80.62727 -29.3188 1116.417
0.02 72.76079 25.74116 1114.589
0.03 10.4081 -8.38121 1100.086
0.04 37.90999 78.65837 1114.397
0.05 33.6431 -13.6943 1103.762
0.06 93.01123 -71.8146 1116.176
0.07 90.45526 0.231349 1117.563
0.08 45.8248 24.46634 1107.898

图1问题二导航结果可视化

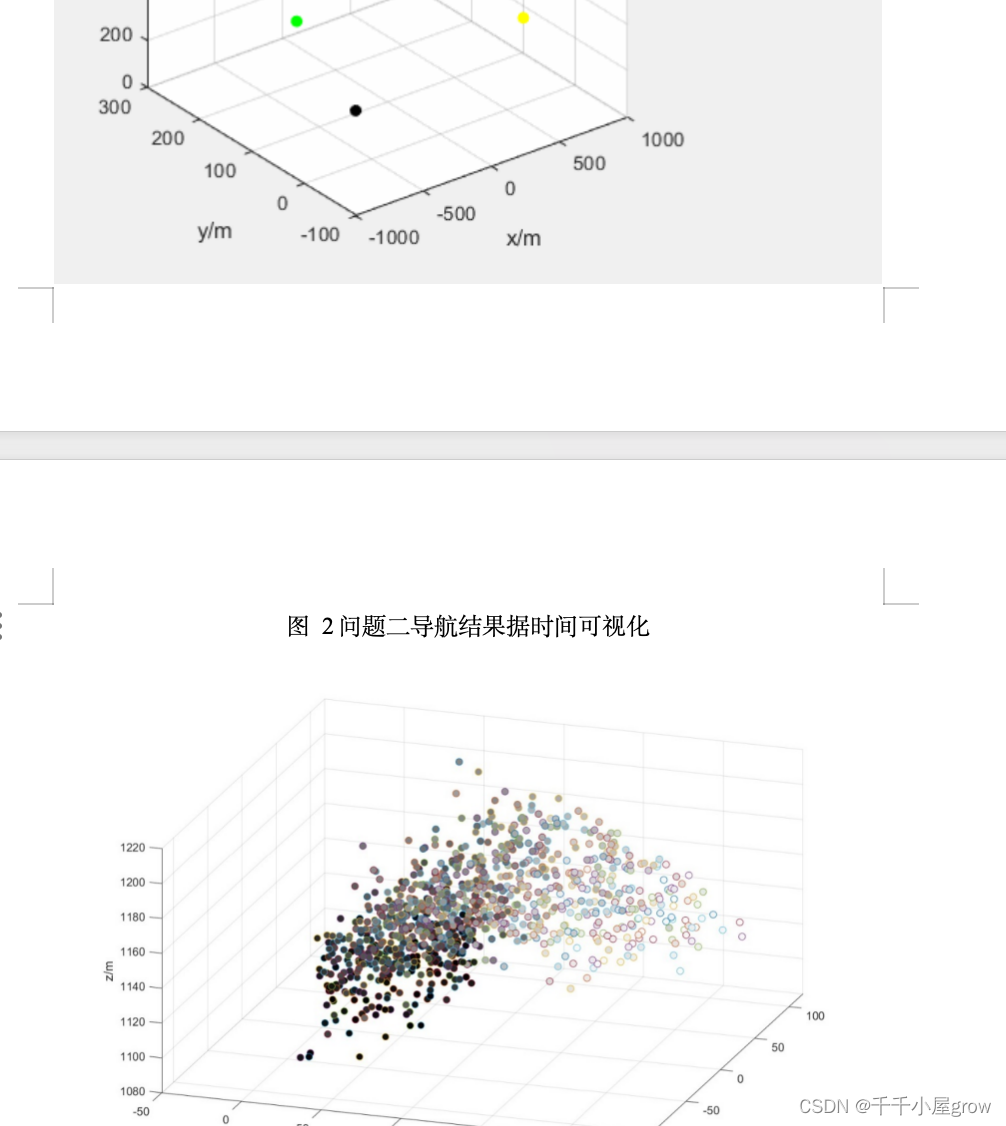
图2问题二导航结果据时间可视化

图2展示了根据数值结果预测的飞行器轨迹路线其中较早的时间用浅色表示，较晚的时间用较深的颜色表示。这种可视化帮助观察者理解随时间演变的趋势或模式。可以看出飞行器大致是朝着xy减小，高度大致不变的方向运动

问题三
实时筛选机会信号：
机会信号中的TOA（Time of Arrival）和 RSSI（Received Signal Strength Indicator）分析：
TOA和RSSI都是在无线通信和定位系统中使用的技术，用于估计设备的位置。尽管它们的目的相同，但这两种技术在实现、准确性和受环境影响的方式上有显著差异。

面对数据误差的处理
处理带有误差的数据确定导航位置时，RSSI可能更具挑战性，因为它受环境因素的影响更大，而这些环境因素往往难以预测和量化。相比之下，尽管TOA也需要高精度的时间测量设备和良好的同步，但它的误差类型通常更容易通过技术手段（如改进硬件或使用更精确的时钟）进行控制和补偿。
由于RSSI与TOA的数据能够同时转换为距离数据，因此两者不同的数据会使得预测的困难。因此我们可以给它们同样的评价方式来选取每次获取的新信号中偏差更小的机会信号。因为DFD和AOA的信息无法独立或者联合求解出导航器的位置，同时我们将TDOA与TOA归纳为同一类机会信号（统一用TOA代表）。图3展示了数据1中发射源123的TOA与RSSI距离数据之差的数据。
图3：发射源1,2,3TOA-RSSI差距比较

从图中看出发射源1的误差最小，发射源2的误差较小，发射源3的误差最大，所以某种程度上，发射源3的信息并不可靠。图4展示了问题二结果的最大误差范围。
通过图4我们可以通过问题二的数据获取的最大误差范围叠加图，我们可以从图中看出，数据的偏差十分巨大，导致误差范围已经远大于飞行器运动的范围，这说明某些机会信号参数收到各种因素影响，导致整体的偏差十分巨大。因此，必须去除这些因素的影响。
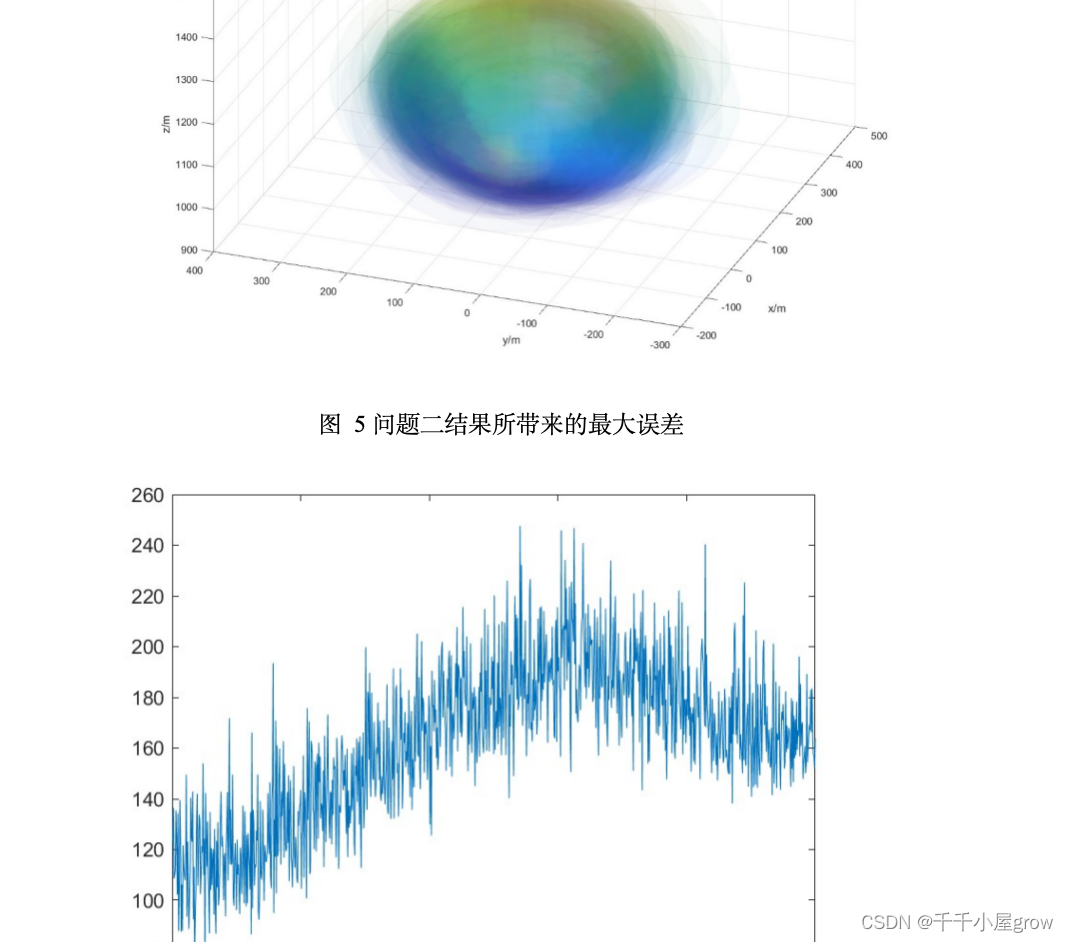
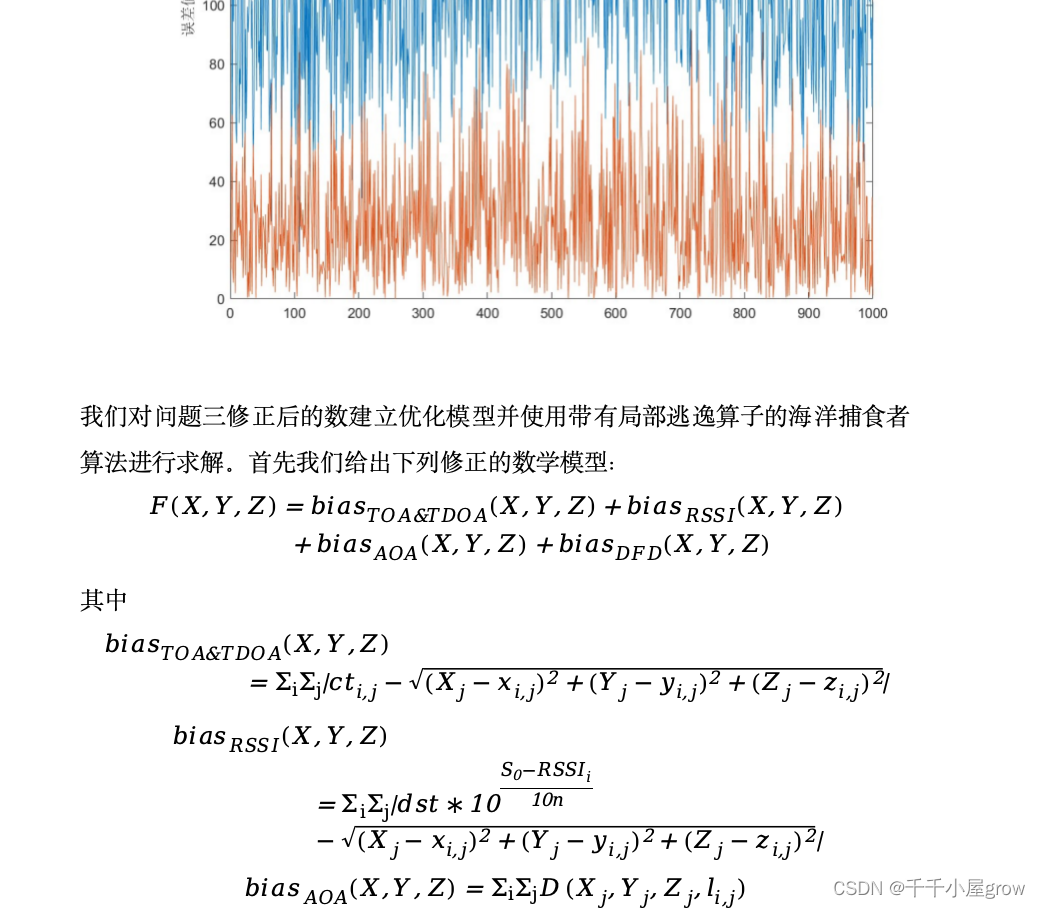
图5展示了问题二求解结果所带来的最大误差，从中我们可以看出误差的整体走向是先增高后降低，并且总是保持较高水平这说明，数据的偏差存在一部分是常值飘移的。同时误差的振动也保持一个相对固定的幅度，这说明误差中也存在随机性偏差。图6问题二结果所带来的各项误差，通过图6可以看出，虽然发射源3的RSSI和TOA差距较大，但是产生最大的误差的数据来源于发射源1。同时通过对发射源3TOA数据的修正对比见图7可以知道发射源3TOA数据确实带来了巨大的误差，因此可以筛除。

图4最大误差范围叠加图、

在相关的论文中[
Oszust, Mariusz. “Enhanced marine predators algorithm with local escaping operator for global optimization.” Knowledge-Based Systems 232 (2021): 107467.]已经说明LEO-MPA的性能由于PSO，因此我们选取LEO-MPA来求解该问题。由于LEO-MPA算法的捕食者数目参数过高会导致计算时间过长，因此，我们选取相比PSO更少的捕食者数目，并增加最大迭代次数。实际上，这样配置下的LEO-MPA算法具有更快的速度以及更好的结果。
算法配置：捕食者数目：10000
最大迭代次数：2500
算法结果：误差函数值：0.553图8展示了LEOMPA求解所获得的轨迹图像,可以看出轨迹比之前问题二的结果更加集中并且有明显的方向信息。因此，通过对大偏差数据的处理，我们可以获取更准确的飞行器轨迹预测。

表2问题三LEOMPA求解部分结果
时间/s X坐标/m Y坐标/m Z坐标/m
0.01 48.91986 1.920731 218.4599
0.02 55.54527 5.703577 171.2798
0.03 42.5561 3.960683 158.8403
0.04 46.24115 17.63549 219.0505
0.05 44.39085 6.711485 208.9762
0.06 55.72649 -0.96734 102.17
0.07 40.50974 15.96831 174.7587
0.08 33.4839 26.37803 89.122

图8 问题三LEOMPA求解轨迹

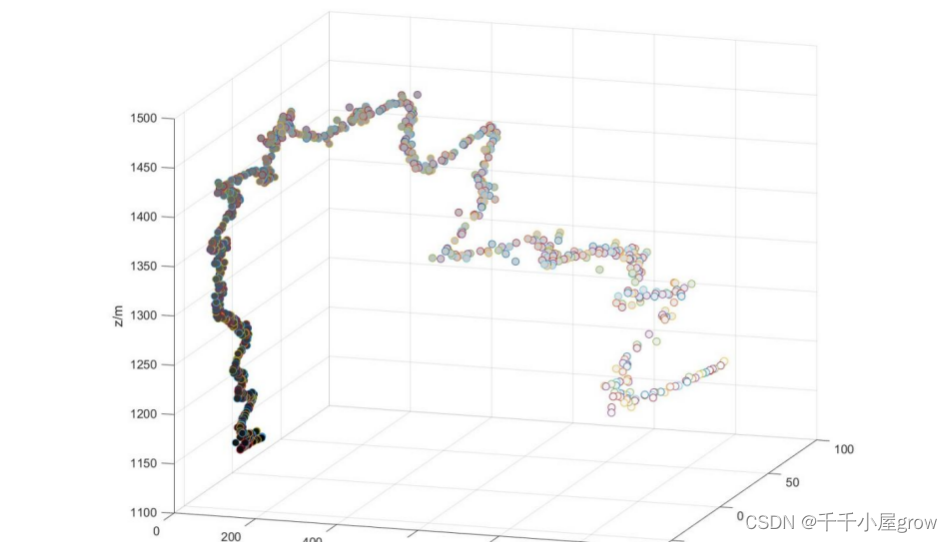
问题四

随机偏差的处理
我们采用简单移动平均（Simple Moving Average，SMA）。SMA是一种常用的数据平滑技术，特别适用于时间序列数据，用于降低数据中的随机波动并揭示潜在的趋势。这种方法通过计算一定时间窗口内数据点的算术平均值来实现数据平滑。
工作原理
简单移动平均的计算过程非常直接：
选择窗口大小：确定包含多少个连续数据点的平均值。窗口大小（N）是一个重要的参数，因为它决定了平滑的程度和反应速度。窗口越大，平滑效果越明显，但对数据中变化的反应速度越慢。
计算平均值：对于时间序列中的每个点，取该点及其前N-1个数据点的平均值。对于序列的开始部分，直到累积到足够的数据点，才能开始计算移动平均。
滑动窗口：窗口沿着数据序列逐步滑动，每次向前移动一个数据点，并重新计算当前窗口内的平均值。

##【腾讯文档】2024数维杯助攻合集
## https://docs.qq.com/doc/DVVBER216eHJKc29y