我最近准备以陈姥姥的数据结构教材为蓝本重新学一下数据结构,写一下读书笔记
第1章 概论
1.1 引子
概论中首先描述了,数据结构的定义没有具体的定义,初学者可以不用管这个定义的问题,但是我理解的和维基百科的说法是一样的“数据结构是计算机中存储、组织数据的方式。通常情况下,精心选择的数据结构可以带来最优效率的算法。”
在这个笔记中,我的代码均使用纯C语言。
然后做了两段代码的对比,以此来说明算法运行时间(即时间复杂度)的重要性,先执行循环的,输入N为9999999
#include <stdio.h>
// 循环打印1到N的全部整数
void CirPrintN(int N)
{
int i = 0;
for(i = 1; i<=N; i++)
{
printf("%d\n", i);
}
}
// 递归打印1到N的全部整数
void RecPrintN(int N)
{
if(N>0)
{
RecPrintN(N-1);
printf("%d\n", N);
}
}
int main()
{
int N = 0;
scanf("%d", &N);
CirPrintN(N);
return 0;
}
循环版本的运行结果:

可以看到,循环版本是可以正常打印的
递归的版本出现异常,原因是它每一次递归都要保存当前的状态到递归调用栈中,所以它需要占用大量的内存空间,一旦数据量大,内存空间就不足了

然后又对比了秦九韶算法和普通的正常一次循环遍历的多项式求和算法(即求
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n
x
n
f(x)=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}
f(x)=a0+a1x+a2x2+...+anxn)
秦九韶算法是这样的,对于如下的多项式:
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n
−
1
x
n
−
1
+
a
n
x
n
=
a
0
+
x
(
a
1
+
a
2
x
+
.
.
.
+
+
a
n
−
1
x
n
−
2
+
a
n
x
n
−
1
)
=
a
0
+
x
(
a
1
+
x
(
a
2
+
.
.
.
+
a
n
−
1
x
n
−
3
+
a
n
x
n
−
2
)
)
=
.
.
.
=
a
0
+
x
(
a
1
+
x
(
a
2
+
.
.
.
+
x
(
a
n
−
1
+
a
n
x
)
.
.
.
)
)
f(x)=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n-1}x^{n-1}+a_{n}x^{n}\newline =a_{0}+x(a_{1}+a_{2}x+...++a_{n-1}x^{n-2}+a_{n}x^{n-1})\newline =a_{0}+x(a_{1}+x(a_{2}+...+a_{n-1}x^{n-3}+a_{n}x^{n-2}))\newline =...\newline =a_{0}+x(a_{1}+x(a_{2}+...+x(a_{n-1}+a_{n}x)...))
f(x)=a0+a1x+a2x2+...+an−1xn−1+anxn=a0+x(a1+a2x+...++an−1xn−2+anxn−1)=a0+x(a1+x(a2+...+an−1xn−3+anxn−2))=...=a0+x(a1+x(a2+...+x(an−1+anx)...))
也就是说,我们可以从括号里算到括号外
然后下面对比这两种算法涉及到了C语言的time.h头文件
C语言的 time.h 头文件提供了与时间相关的函数和类型定义。这个头文件常用于获取当前时间、日期,或者进行时间的测量和转换。
clock_t 类型
clock_t 是一个数据类型,通常用于表示“时钟”或“处理器时间”的度量单位。它通常是一个长整型(long 或 long long)的别名,但具体的大小和表示方式可能依赖于系统和编译器。
在 time.h 中,clock_t 类型的值通常由 clock() 函数返回,该函数返回程序执行到该点为止的CPU时间(以“时钟滴答”为单位)。这个值可以用来测量代码段的执行时间。
clock() 函数
clock() 函数返回一个 clock_t 类型的值,表示从程序启动开始到 clock() 被调用时的CPU时间。这个函数通常用于性能分析和基准测试。
CLK_TCK(或 CLOCKS_PER_SEC)
CLK_TCK 或 CLOCKS_PER_SEC 是一个宏定义,它表示 clock() 函数返回的时钟滴答数每秒的个数。换句话说,它定义了 clock_t 类型的值与实际秒数之间的转换因子。用这个宏来将 clock() 的返回值转换为秒数。
下面就是对比运行时间的代码,其中,这里面的*f是函数指针的意思,在C语言中,函数指针是一个特殊的指针,它指向一个函数的入口地址。函数指针可以用来调用函数,或者作为其它函数的参数。
#include <stdio.h>
#include <time.h>
#include <math.h>
clock_t start = 0; //开始时间
clock_t stop = 0; //结束时间
double duration = 0.0; //算法一共运行了多长时间
#define MAXN 10 // 多项式最大项数,即多项式阶数+1
#define MAXK 1e7 // 被测函数最大重复调用次数
// n为多项式的项数,a数组存储的是多项式各系数
//普通的循环法求多项式的和
double f1(int n, double a[], double x)
{
int i = 0;
double p = a[0];
for (i = 1; i <= n; i++)
{
p += (a[i] * pow(x, i));
}
return p;
}
//秦九韶法求多项式的和
double f2(int n, double a[], double x)
{
int i = 0;
double p = a[n];
for (i = n; i > 0; i--)
{
p = a[i - 1] + x * p; //从最里面的括号开始算
}
return p;
}
// 此函数用于测试被测函数*f,并且根据case_n输出相应的结果
// case_n是输出的函数编号:1代表函数f1;2代表函数f2
void run(double (*f)(int, double*, double), double a[], int case_n)
{
int i = 0;
start = clock();
//重复调用函数以获得充分多的时钟打点数
for (i = 0; i < MAXK; i++) // 调用MAXK次
{
(*f)(MAXN - 1, a, 1.1);
}
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK; // 转换为秒数
printf("ticks%d= %f \n", case_n, (double)(stop - start));
printf("duration%d = % 6.2e \n", case_n, duration);
}
int main()
{
int i = 0;
double a[MAXN];
for (i = 0; i < MAXN; i++)
{
a[i] = (double)i;
}
run(f1, a, 1);
run(f2, a, 2);
return 0;
}
运行结果:

传统方法是1.39s,秦九韶算法是
2.01
×
1
0
−
1
2.01\times 10^{-1}
2.01×10−1秒,后者更快
这几个引子目的就是为了说明精心选择的数据结构可以带来最优效率的算法。
1.2 数据结构
1.2.1 定义
陈姥姥的书里讲的定义挺通俗易懂的,我这里直接把严蔚敏书的定义拿过来
- 数据:数据是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
- 数据元素:数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
- 数据对象:数据对象是性质相同的数据元素的集合,是数据的一个子集。例如,整数数据对象是集合 N = { 0 , ± 1 , ± 2 , ⋯ } N=\{0, \pm 1, \pm 2, \cdots\} N={0,±1,±2,⋯}
- 数据结构:数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
通常有4类基本结构“
- 集合:结构中的元素之间除了”同属于一个集合“的关系外,别无其他关系;
- 线性结构:结构中的数据元素直接存在一个对一个的关系;
- 树形结构:结构中的数据元素直接存在一个对多个的关系;
- 图状结构或网状结构:结构中的数据元素之间存在多个对多个的关系。

数据结构在计算机中的表示(又称映像)称为数据的物理结构,又称存储结构。
1.2.2 抽象数据类型
抽象数据类型就是对数据类型的描述,也就是抽象(概括),比如我们要写一个矩阵的数据类型,它的抽象数据类型定义是:
(1)类型名称:矩阵(Matrix)
(2)数据对象集:一个
m
×
n
m\times n
m×n的矩阵
A
m
×
n
=
(
a
i
j
)
(
i
=
1
,
.
.
.
,
m
,
j
=
1
,
.
.
.
,
n
)
A_{m\times n}=(a_{ij})(i=1, ..., m, j=1, ..., n)
Am×n=(aij)(i=1,...,m,j=1,...,n)由
m
×
n
m\times n
m×n个三元组<a, i, j>构成,其中
a
a
a是矩阵元素的值,
i
i
i是元素所在的行号,
j
j
j是元素所在的列号。
(3)操作集:就是列出矩阵都有什么基本运算(操作)
- Matrix Create(int M, int N); //返回一个MxN的空矩阵
- int GetMaxRow(Matrix A); //返回矩阵A的总行数
……
等等
操作集是忽略操作的代码实现细节的,只需要关注其有什么功能即可。
1.3 算法
1.3.1 定义
一般而言,算法是一个有限指令集,它接受一些输入(有些情况下不需要输入),产生输出,并一定在有限步骤之后终止。
1.3.2 算法复杂度
- 空间复杂度 S ( n ) S(n) S(n)——根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模 n n n有关。空间复杂度过高的算法可能导致使用的内存超出限制而造成程序非正常中断。
- 时间复杂度 T ( n ) T(n) T(n)———根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入的规模 n n n有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。
刚才两个例子就说明了算法时间复杂度的问题。
在分析一般算法的效率时,我们经常关注下面两种复杂度:
(1)最坏情况复杂度
T
w
o
r
s
t
(
n
)
T_{worst}(n)
Tworst(n)
(2)平均复杂度
T
a
v
g
(
n
)
T_{avg}(n)
Tavg(n)
对 T w o r s t ( n ) T_{worst}(n) Tworst(n)分析比对 T a v g ( n ) T_{avg}(n) Tavg(n)分析容易,我们一般分析最坏复杂度。
1.3.3 渐进表示法
渐进表示法是我们分析复杂度的主要表示法,书中提到的上界函数下界函数暂时不用考虑,用大写字母
O
O
O表示渐进的复杂度,一个语句的频度是指该语句在算法中被重复执行的次数。算法中所有语句的频度之和记为
T
(
n
)
T(n)
T(n),它是该算法问题规模
n
n
n的函数,算法的时间复杂度主要分析
T
(
n
)
T(n)
T(n)的数量级,也就是分析
T
(
n
)
T(n)
T(n)与哪些初等的简单函数为同阶无穷大。通常采用算法中基本运算的频度
f
(
n
)
f(n)
f(n)来分析算法的时间复杂度。因此,算法的时间复杂度记为:
T
(
n
)
=
O
(
f
(
n
)
)
T(n)=O(f(n))
T(n)=O(f(n))
在微积分中,我们学过,当
n
→
∞
n\to \infty
n→∞时,有如下的不等式:
ln
n
<
n
a
<
b
n
<
n
!
<
n
n
(
a
>
0
,
b
>
1
)
\text{ln}n<n^{a}<b^{n}<n!<n^{n}(a>0,b>1)
lnn<na<bn<n!<nn(a>0,b>1)
最后展开详细说就是:
O
(
1
)
<
O
(
log
2
n
)
<
O
(
n
)
<
O
(
n
log
2
n
)
<
O
(
n
2
)
<
O
(
n
3
)
<
O
(
2
n
)
<
O
(
n
!
)
<
O
(
n
n
)
O(1)<O\left(\log _{2} n\right)<O(n)<O\left(n \log _{2} n\right)<O\left(n^{2}\right)<O\left(n^{3}\right)<O\left(2^{n}\right)<O(n!)<O\left(n^{n}\right)
O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
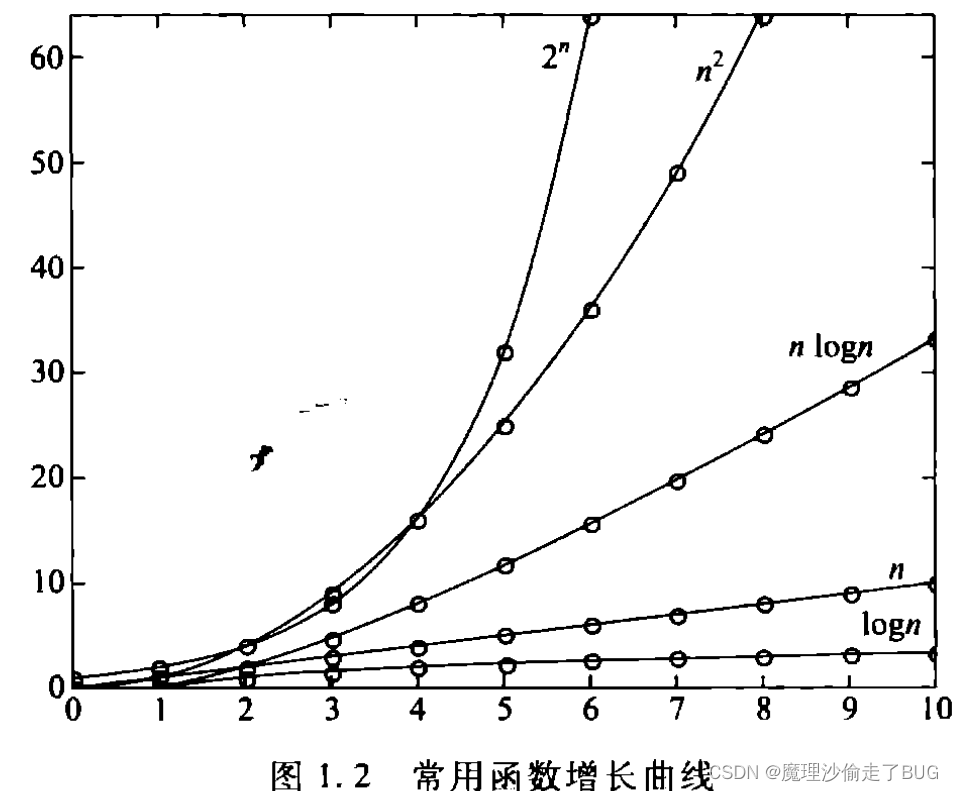
正好也对应着书中的常用函数增长曲线
对于做渐进时间复杂度分析时,有5个规律:
(1)若两段算法分别有复杂度
T
1
(
n
)
=
O
(
f
1
(
n
)
)
T_{1}(n)=O(f_{1}(n))
T1(n)=O(f1(n))和
T
2
(
n
)
=
O
(
f
2
(
n
)
)
T_{2}(n)=O(f_{2}(n))
T2(n)=O(f2(n)),那么:两段算法串联在一起的时间复杂度为
max
O
(
f
1
(
n
)
)
,
O
(
f
2
(
n
)
)
\text{max}{O(f_{1}(n)), O(f_{2}(n))}
maxO(f1(n)),O(f2(n)),也就是取时间复杂度最大的;若两段算法嵌套在一起(循环里嵌套循环那种):则时间复杂度为
O
(
f
1
(
n
)
f
2
(
n
)
)
O(f_{1}(n)f_{2}(n))
O(f1(n)f2(n))(相乘)
比如,有如下代码:
int i = 1, k = 0;
while (i <= n - 1)
{
k += 10 * i;
i++;
}
对于上述代码来说,其while循环执行了n-1次,则其时间复杂度为
O
(
n
−
1
)
O(n-1)
O(n−1)又根据同阶无穷大的原则,最终(1)的时间复杂度为
O
(
n
)
O(n)
O(n)
再比如,有如下代码:
int i=0,k = 0,j=0;
for (i = 1; i <= n; i++)
{
for (j = i; k <= n; j++)
{
k++;
}
}
上述代码共有两层for循环,外层循环执行了n次,而外层循环每执行一次里层循环都执行n次,这样外层循环执行次数与内层循环执行次数相乘即为答案,故它的时间复杂度为
O
(
n
2
)
O(n^{2})
O(n2);
(2)若
T
(
n
)
T(n)
T(n)是关于
n
n
n的
k
k
k阶多项式,那么
T
(
n
)
=
O
(
n
k
)
T(n)=O(n^{k})
T(n)=O(nk);
(3)一个for循环的时间复杂度等于循环次数乘以循环体代码的复杂度。例如这个循环的复杂度是
O
(
n
)
O(n)
O(n):
for(int i = 0; i< N;i++)
{
x = y*x+z;
k++;
}
(4)若干层嵌套循环的时间复杂度等于各层循环次数的乘积再乘以循环体代码的复杂度,例如下列2层嵌套循环的复杂度是 O ( n 2 ) O(n^{2}) O(n2):
for(int i = 0; i< N;i++)
{
for(int j =0; j< N;j++)
{
x = y*x+z;
k++;
}
}
(5)if-else结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度,总体复杂度取三者中最大,即对结构:
if(P1):
P2;
else:
P3;
总复杂度为
O
(
max
(
f
1
,
f
2
,
f
3
)
)
O(\text{max}(f_{1},f_{2},f_{3}))
O(max(f1,f2,f3)),其中
f
i
,
i
=
1
,
2
,
3
f_{i},i=1,2,3
fi,i=1,2,3代表
P
i
P_{i}
Pi的复杂度。
1.4 应用实例:最大子列和问题
这个问题与LeetCode53最大子数组和是类似的,只是在关于最终求和是负数的问题上处理的不一样,陈姥姥的书中是这样描述问题的,给定 n n n个整数的序列 a 1 , a 2 , . . . , a n a_{1}, a_{2}, ..., a_{n} a1,a2,...,an,求函数 f ( i , j ) = max { 0 , ∑ k = i j a k } f(i, j)=\max \left\{0, \sum\limits_{k=i}^{j} a_{k}\right\} f(i,j)=max{0,k=i∑jak},也就是,我们要寻找的是具有最大和的一段连续的子列,并且返回它的和。如果这个最大和是负数,那么我们取0为最终答案(LeetCode则在此种情况下返回负数最大和)。例如给定序列{-2, 11, -4, 13, -5, 2},其最大子列为{11, -4, 13},和为20.
1.4.1 暴力法
暴力法就是穷举所有子列的和,从中找出最大值,代码如下:
#include <stdio.h>
//暴力法
int MaxSubseqSum1(int List[], int N)
{
int ThisSum = 0; //当前子列的和
int MaxSum = 0; //最大子列和,默认赋值为0,如果和为负数,就只能返回0
//i是子列左端位置
for (int i = 0; i < N; i++)
{
//j是子列右端位置
for (int j = i; j < N; j++)
{
ThisSum = 0;
// 把子列和(从List[i]加到List[j])加一起
for (int k = i; k <= j; k++)
{
ThisSum += List[k];
}
// 如果当前和超过之前的最大和,则最大和赋值成这个
if (ThisSum > MaxSum)
{
MaxSum = ThisSum;
}
}
}
return MaxSum;
}
int main()
{
int a[6] = { -2, 11, -4, 13, -5, -2 };
printf("%d\n", MaxSubseqSum1(a, 6));
int b[3] = { -2, -4, -5};
printf("%d\n", MaxSubseqSum1(b, 3));
return 0;
}
暴力法三层for循环,时间复杂度更是看一眼多一眼就会爆炸的 O ( n 3 ) O(n^{3}) O(n3),其实这么写暴力法完全没必要,主要是从List[i]加到List[j]的过程没必要,我们返回的是最大子列和而不是返回最大子列的所有的元素,所以,我们完全可以从j那个循环下手,直接让ThisSum+=List[j],然后再比较大小,这样就算j的继续遍历到下一个使得ThisSum和变小了,我们也不用担心,因为根本不会进入if条件导致MaxSum赋值为这个变小了的ThisSum,我们求的只是子列和,不是子列的元素,这一点要记住,所以这个暴力法还能优化成一个时间复杂度为 O ( n 2 ) O(n^{2}) O(n2)的暴力法,即:
#include <stdio.h>
//暴力法2
int MaxSubseqSum2(int List[], int N)
{
int ThisSum = 0; //当前子列的和
int MaxSum = 0; //最大子列和,默认赋值为0,如果和为负数,就只能返回0
//i是子列左端位置
for (int i = 0; i < N; i++)
{
ThisSum = 0; // ThisSum清零的工作就放到了j这个循环的外层
//j是子列右端位置
for (int j = i; j < N; j++)
{
ThisSum += List[j];
// 如果当前和超过之前的最大和,则最大和赋值成这个
if (ThisSum > MaxSum)
{
MaxSum = ThisSum;
}
}
}
return MaxSum;
}
int main()
{
int a[6] = { -2, 11, -4, 13, -5, -2 };
printf("%d\n", MaxSubseqSum2(a, 6));
int b[3] = { -2, -4, -5};
printf("%d\n", MaxSubseqSum2(b, 3));
return 0;
}
但是这仍然不是时间复杂度最好的算法。
1.4.2 分治法
顾名思义,分而治之法的基本思路就是将问题拆成若干小问题,分别解决后再将结果合起来,用递归实现非常方便。我们可以把这个问题的原始序列一分为二,那么最大子列或者在左半边或者在右半边,或者是横跨中分线的一段。于是我们得到了这个算法的步骤:
- 将序列从中分为左右两个子序列;
- 递归(或循环)求得两子列的最大和 S 左 S_{左} S左和 S 右 S_{右} S右;
- 从中分点分头向左、右两边扫描,找出跨过分界线的最大子列和 S 中 S_{中} S中;
- S max = max { S 左 , S 右 , S 中 } S_{\text{max}}=\text{max}\{S_{左}, S_{右}, S_{中}\} Smax=max{S左,S右,S中}
这个分治法用循环去解太难想了,我根据它的描述和书中的代码,写了一段代码,加了详细的注释:
// 比较三个数中最大数的宏定义
#define MAX3(A, B, C) (( A > B ? A : B) > C) ? ( A > B ? A : B) : C
// 分治法递归求最大子列和
int DivideAndConquer(int* List, int left, int right)
{
int MaxLeftSum = INT_MIN; // 左子列的最大和
int MaxRightSum = INT_MIN; // 右子列的最大和
int MaxLeftBorderSum = INT_MIN; //跨越中点的子列的左侧的和
int MaxRightBorderSum = INT_MIN; //跨越中点的子列的右侧的和
int LeftBorderSum = 0; //跨越中点的子列的左侧的和(不一定是最大的)
int RightBorderSum = 0; //跨越中点的子列的右侧的和
int middle = 0; //分治法求分界点的变量s
// left与right重合时,递归停止,也就是子列只有一个数字
// 这是最小的子列,其和就是这一个元素,如果它的和
// 也就是这一个元素为负数或者0,则应该返回0(根据题意)
// 如果是LeetCode53,则应该直接返回List[left],不需要加判断条件
// 因为LeetCode53是需要对比负数和的
if(left == right)
{
if(List[left] > 0)
{
return List[left];
}
else
{
return 0;
}
}
// 求解中点,向右移动一位相当于除2
middle = (right + left)>>1; // 此处也可以等价成(right - left)/2 + left,但是这样写会超时
//递归求解左子列和右子列的最大和
MaxLeftSum = DivideAndConquer(List, left, middle);
MaxRightSum = DivideAndConquer(List, middle + 1, right);
//求跨越中点的子列的最大和
MaxLeftBorderSum = INT_MIN; //每次求和之前,要将最大值变为无穷小,方便比较
LeftBorderSum = 0;
//找跨越中点的子列的左侧的最大和(从中点向左遍历)
for(int i = middle; i>=left; i--)
{
LeftBorderSum += List[i];
if(LeftBorderSum > MaxLeftBorderSum)
{
MaxLeftBorderSum = LeftBorderSum;
}
}
//找跨越中点的子列的右侧的最大和(从中点向右遍历)
MaxRightBorderSum = INT_MIN; //每次求和之前,要将最大值变为无穷小,方便比较
RightBorderSum = 0;
for(int i = middle + 1; i<=right; i++)
{
RightBorderSum += List[i];
if(RightBorderSum > MaxRightBorderSum)
{
MaxRightBorderSum = RightBorderSum;
}
}
// 返回左子列,跨越中点的子列和右子列三者中的最大值
return MAX3(MaxLeftSum, MaxLeftBorderSum + MaxRightBorderSum, MaxRightSum);
}
int maxSubArray(int* List, int N) {
return DivideAndConquer(List, 0, N-1);
}
按分治法所说,这是不断地二分求解子问题,相当于是每次都分为
1
2
\frac{1}{2}
21,那么假设这个算法的整体的时间复杂度为
T
(
n
)
T(n)
T(n),则DivideAndConquer函数中递归进行分治的复杂度为
2
T
(
n
2
)
2T(\frac{n}{2})
2T(2n),因为我们是对左右两个子列不断二分求解,相当于解决了2个长度减半的子问题(就是那两个递归地求左子列最大和以及右子列最大和的过程,这相当于以
n
2
\frac{n}{2}
2n的规模再调用函数,也就是递归二分的过程,所以求单侧最大和的复杂度是
T
(
n
2
)
T(\frac{n}{2})
T(2n)),求跨越分界线的最大子列和时,相当于求解了两个最坏复杂度为
O
(
n
2
)
O(\frac{n}{2})
O(2n)的问题,也就是最坏时间复杂度为
O
(
n
2
+
n
2
=
n
)
=
O
(
n
)
O(\frac{n}{2}+\frac{n}{2}=n)=O(n)
O(2n+2n=n)=O(n)的问题,那么它整体的时间复杂度为:
T
(
n
)
=
2
T
(
n
2
)
+
O
(
n
)
=
2
[
2
T
(
n
2
2
)
+
O
(
n
2
)
]
+
O
(
n
)
=
2
2
T
(
n
2
2
)
+
2
O
(
n
)
=
.
.
.
=
2
k
T
(
n
2
k
)
+
k
O
(
n
)
T(n)=2T(\frac{n}{2})+O(n)\newline =2[2T(\frac{\frac{n}{2}}{2})+O(\frac{n}{2})]+O(n)\newline =2^{2}T(\frac{n}{2^{2}})+2O(n)\newline =...\newline =2^{k}T(\frac{n}{2^{k}})+kO(n)
T(n)=2T(2n)+O(n)=2[2T(22n)+O(2n)]+O(n)=22T(22n)+2O(n)=...=2kT(2kn)+kO(n)
当我们不断地递归,直到递归到问题规模为1的时候,即
n
2
k
=
1
\frac{n}{2^{k}}=1
2kn=1,
n
=
2
k
n=2^{k}
n=2k时
k
=
log
2
n
k=\text{log}_{2}{n}
k=log2n,就能得到
T
(
n
)
=
2
k
T
(
n
2
k
)
+
2
O
(
n
)
=
2
log
2
n
T
(
1
)
+
log
2
n
×
O
(
n
)
=
n
T
(
1
)
+
O
(
n
)
log
2
n
=
n
×
1
+
O
(
n
log
2
n
)
=
O
(
n
+
n
log
2
n
)
=
O
(
n
log
2
n
)
T(n)=2^{k}T(\frac{n}{2^{k}})+2O(n)=2^{\text{log}_{2}{n}}T(1)+\text{log}_{2}{n}\times O(n)=nT(1)+O(n)\text{log}_{2}{n}=n\times1+O(n\text{log}_{2}{n})=O(n+n\text{log}_{2}{n})=O(n\text{log}_{2}{n})
T(n)=2kT(2kn)+2O(n)=2log2nT(1)+log2n×O(n)=nT(1)+O(n)log2n=n×1+O(nlog2n)=O(n+nlog2n)=O(nlog2n),所以这种算法的时间复杂度为
O
(
n
log
2
n
)
O(n\text{log}_{2}{n})
O(nlog2n)
1.4.3 在线处理(动态规划)
“在线”的意思是指每输入一个数据就进行即时处理,得到结果是对于当前已经读入的所有数据都成立的解,即再任何一个地方终止输入,算法都能正确给出当前的解。
前面所给出的3种算法都必须等所有的
N
N
N个整数都读入并存储后才可以进行,而在线处理的方法甚至无须存储输入序列就可以得到任何时刻的最大子列和。
该算法的核心思想是基于下面的事实:如果整数序列
{
a
1
,
a
2
,
⋯
,
a
n
}
\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}
{a1,a2,⋯,an}的最大子列和是
{
a
i
,
a
i
+
1
,
⋯
,
a
j
}
\left\{a_{i}, a_{i+1}, \cdots, a_{j}\right\}
{ai,ai+1,⋯,aj},那么必定有
∑
k
=
i
l
a
k
⩾
0
\sum\limits_{k=i}^{l} a_{k} \geqslant 0
k=i∑lak⩾0对任意
i
⩽
l
⩽
j
i \leqslant l \leqslant j
i⩽l⩽j成立,因此,一旦发现当前子列和为负,则可以重新开始考察一个新的子列。代码如下:
int maxSubArray(int* nums, int numsSize){
int result=0;//最开始假定最大值为0,因为这个题目要求的是负数和算为0,如果和LeetCode53一样需要负数和,此处应设置为INT_MIN
int count =0;//子数组的求和结果
for(int i=0;i<numsSize;i++)
{
count = count + nums[i];
//count大于假定的最大值,就让假定的最大值等于count
if(count > result)
{
result = count;
}
//加和小于等于0,则其不是最大连续子序列,让count从0开始加
//如果加和变成负数,说明从nums[i]开始向前到nums[0]的数无论怎么取连续子数组都只能小于等于result
//result记录的是nums[i]之前的数字的最大连续子数组的和
//所以,就没必要再回到前面去找加和了,直接从nums[i]向后加和对比
//如果从nums[i]开始到最后的加和中出现了加和大于nums[i]之前的最大连续子数组的和result
//那就让result赋值为nums[i]后面的最大连续子数组的和的值
//这样就找到了最大连续子数组的和
if(count<0)
{
count =0;
}
}
return result;
}
该算法只有一层规模为 n n n的for循环,故其时间复杂度为 O ( n ) O(n) O(n),这个例子是告诉大家,解决同一个问题,不同的算法会有很大的差别,让计算机记住一些中间的计算结果,可以避免重复计算。
![[已解决]ModuleNotFoundError: No module named ‘tqdm‘](https://img-blog.csdnimg.cn/direct/1545896e0e954d64b40ef3e4b4ffc355.png)