项目链接

GitHub - cloneofsimo/lora: Using Low-rank adaptation to quickly fine-tune diffusion models.

现在如果想体验stable diffusion的lora功能，有很多种渠道吧，虽然lora是微软开源，但是cloneofsimo提供了适配stable diffusion的lora流程。

数据准备

我准备了20张葫芦娃的图片用于微调，没有什么特别操作。

微调

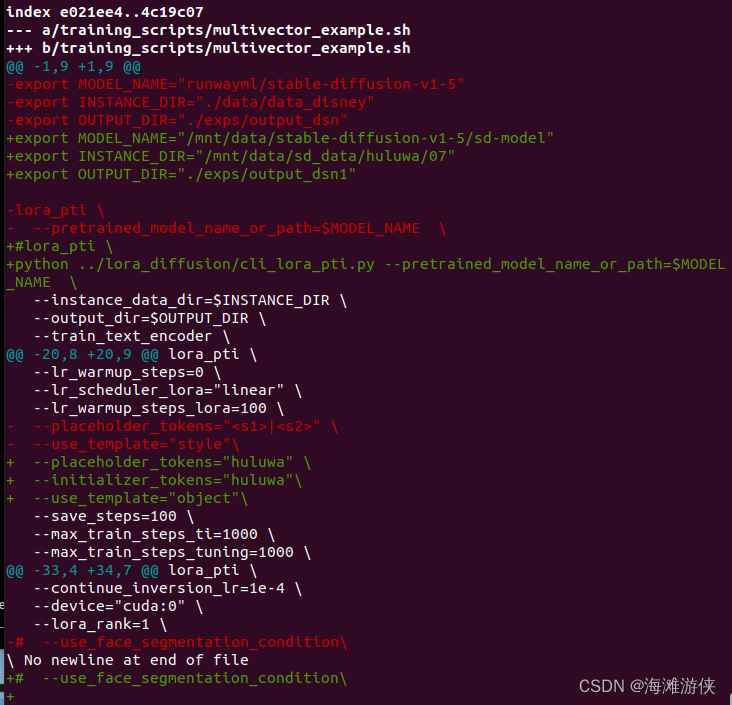
微调耗时很短，10分钟？

Code Review

代码基于cli_lora_pti.py 执行， 针对输入的关键词，我们生成对应的token id. 其实就是建立embedding的映射了。

这里有点不理解的是，initialize_token_ids, place_token_ids的作用不太理解。。。

接下来，进入

PivotalTuningDatasetCapation

它的作用就是构建数据集。

接下来，还有inpaint的训练选项，这是一个我很感兴趣的功能。我们可以选择是使用inpainting_dataloader还是text2img_dataloader 加载数据

然后，我们设定require_grad为false。

   unet.requires_grad_(False)
    vae.requires_grad_(False)

接下来，我们可以选择是否进行inversion， 如果选择训练inversion，我们会对于text encoder进行训练，

接下来，我们可以选择利用lora进行训练,这里可以选择是否使用extended lora进行训练，

然后，我们可以inspect_lora(什么意思呢？

最后，我们又一次进行tuning，对象为text_encoder和unet。并进行保存！我认为这个代码结构非常的清晰简洁，值得多看！

看什么呢？

有几个问题需要再梳理清楚

1. initialized_token_id和place holder token id是什么关系

 2.  inpaint 的操作如何进行？

3. inspect lora是什么操作？

4. inversion的细节

5. extended lora是什么操作？

6. unet微调的细节？

7. vae不需要微调吗？