✨✨✨专栏:数据结构
🧑🎓个人主页:SWsunlight

目录
一、用队列实现栈:
1、2个队列的关联起来怎么由先进先出转变为先进后出:(核心)
2、认识各个函数干嘛用的:
3、代码实现:
二、用栈实现队列:
1、题目:
2、思路:
3、代码:
三、设计循环队列:
1、题目:
2、思路:
编辑
3、代码:
一、用队列实现栈:
内容如下:
2个队列实现栈::首先考虑的是 栈的规则:先进后出(后进先出)
队列的规则:先进先出
1、2个队列的关联起来怎么由先进先出转变为先进后出:(核心)
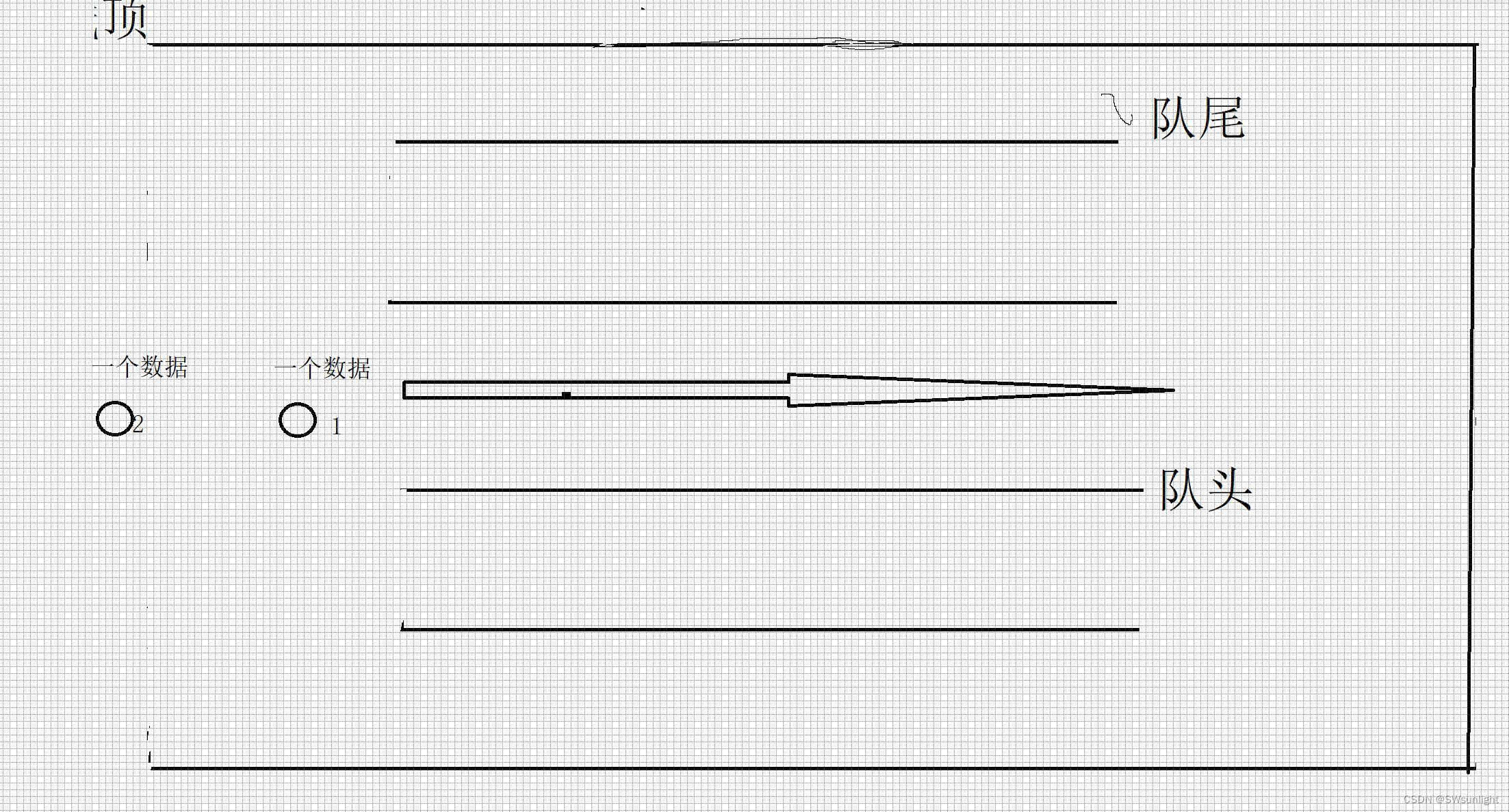
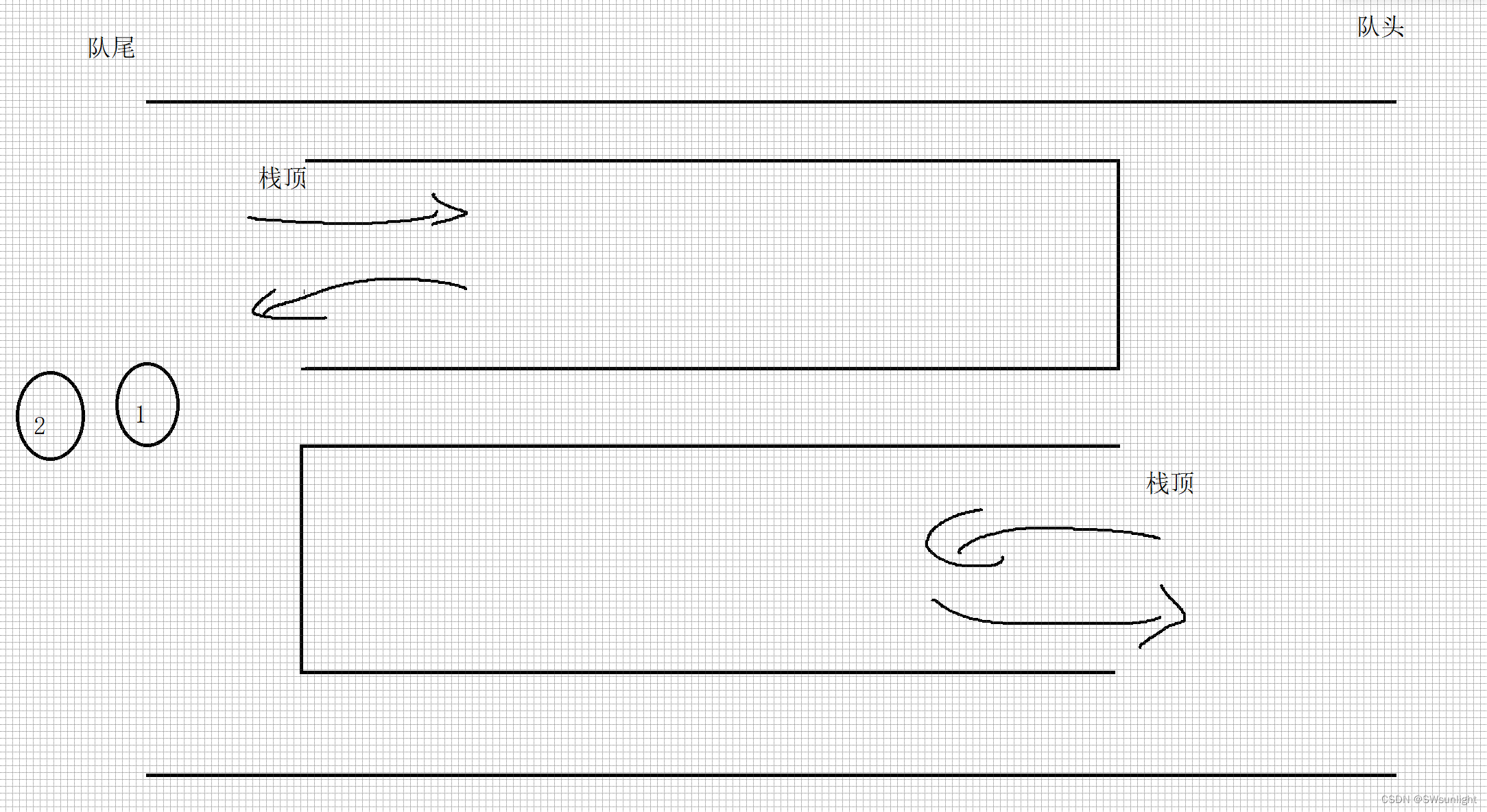
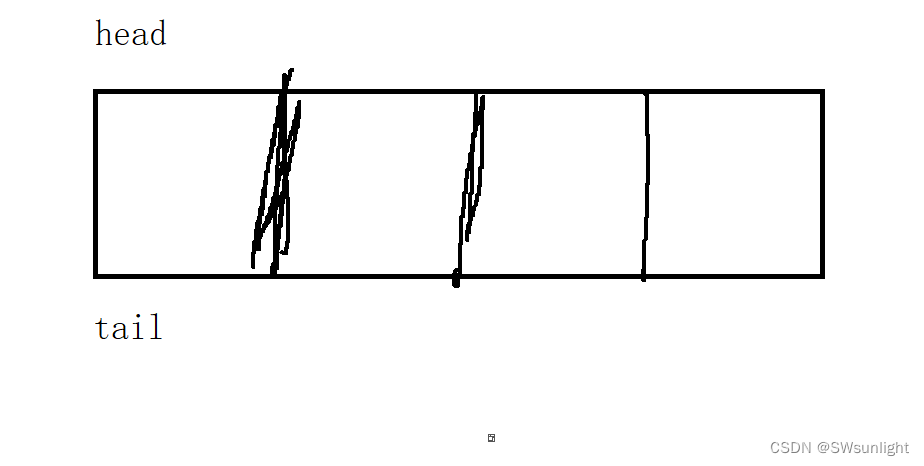
如上图,外围框架(虚构的,为了更好理解,让他具体化)就是我要实现的栈,而我要通过2个队列来实现栈,是不是是可以让小球先走上面的“通道”进去,全部小球(元素)进入上“通道”中,此时我排在通道最后的小球(元素)就是我要出栈的第一个数据。
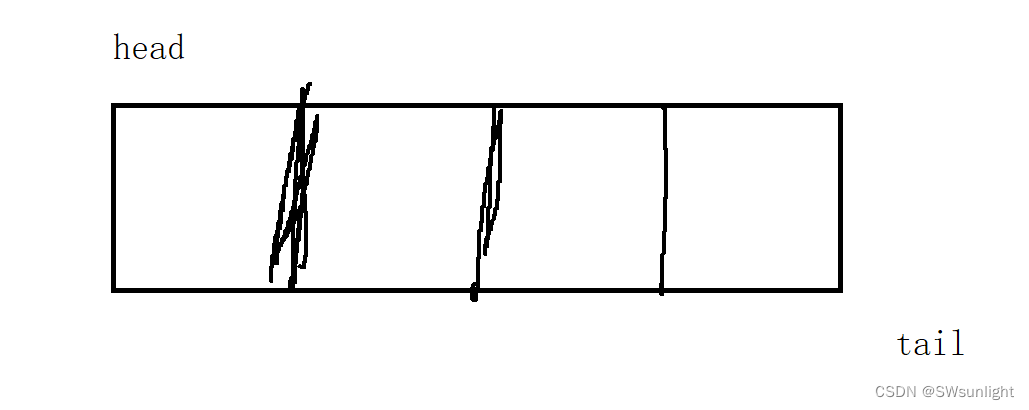
如下图:2号球要第一个出栈,我们发现下“通道”是空的,那么我让2号球前面的球离开这个“通道”去到下面的通道,上通道就会剩下一个2号球,此时取2号球顺利的第一个走出去,就相当于栈的Top(将后进的元素取出)
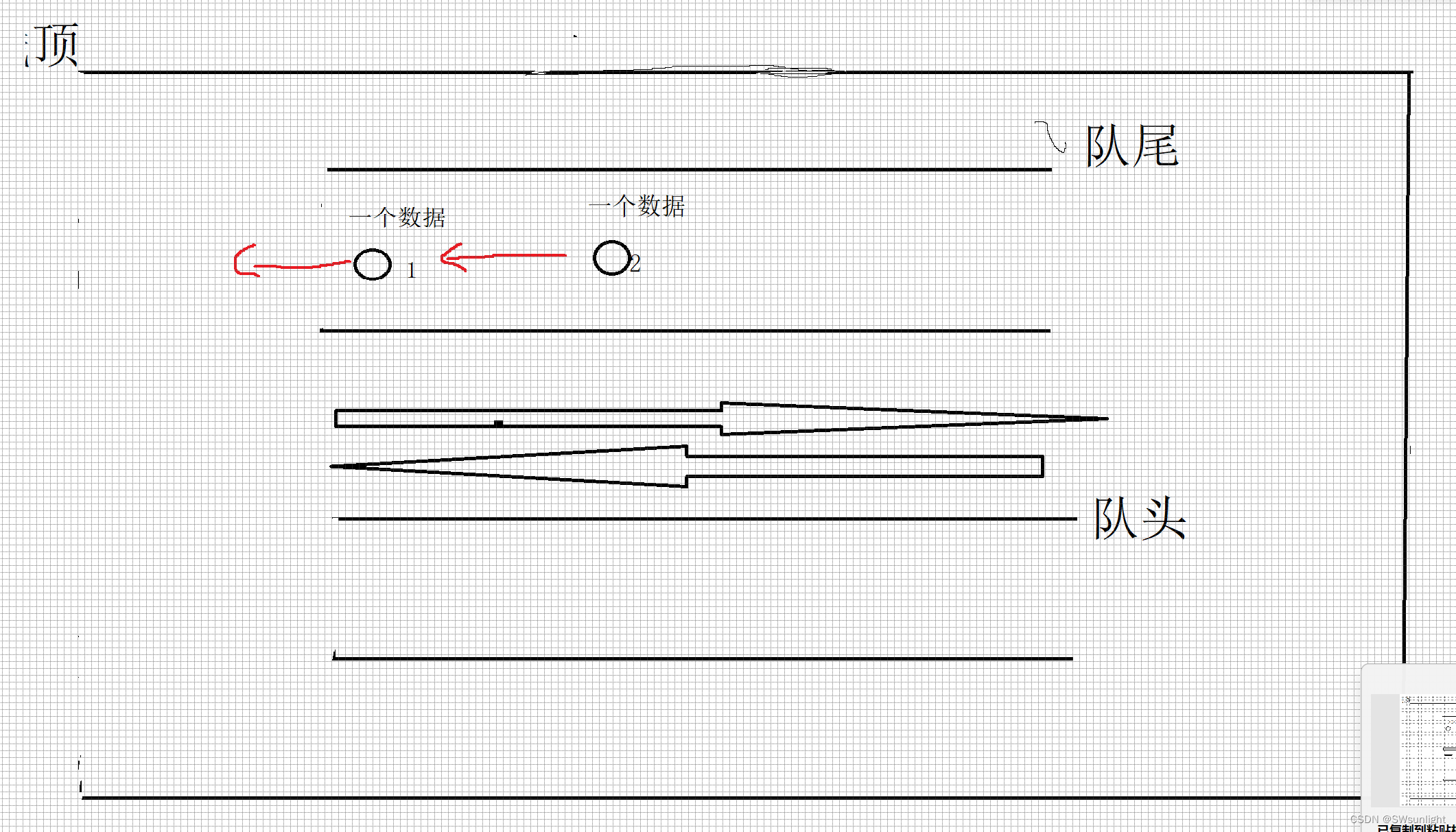
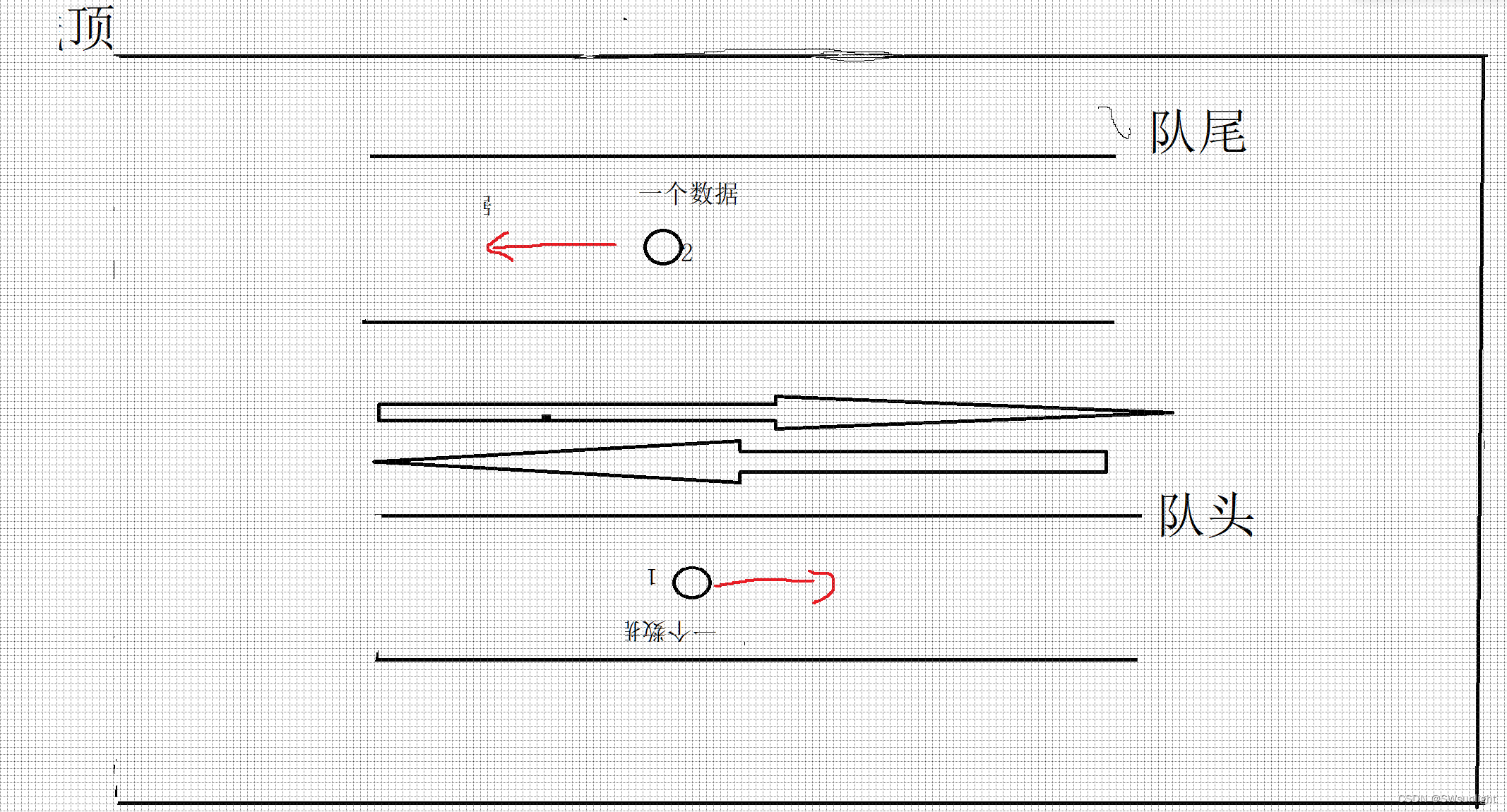 反复进行,就可以实现栈了,(队尾的元素能出栈,其他位置得绕着2个通道来回转(有点像明知她(他)不爱你,你还是要困死再这颗树),只有自己在成为队尾了(心灰意冷了),才会幡然醒悟(不能再一直停留再原地绕圈了,要向前看啦)
反复进行,就可以实现栈了,(队尾的元素能出栈,其他位置得绕着2个通道来回转(有点像明知她(他)不爱你,你还是要困死再这颗树),只有自己在成为队尾了(心灰意冷了),才会幡然醒悟(不能再一直停留再原地绕圈了,要向前看啦)
2、认识各个函数干嘛用的:
可能只是对我而言
我已经标好了,各个函数的功能:知道功能就好实现了
这个结构体的成员放2个队列即可:
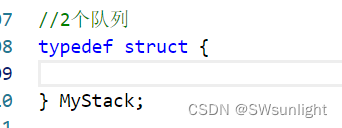

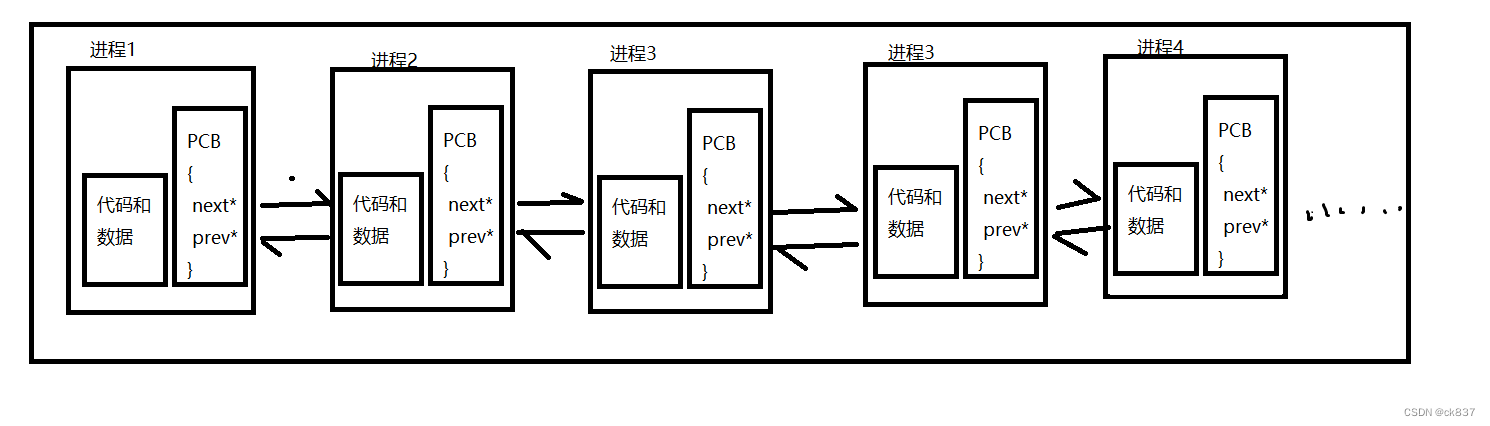
结构体MyStack嵌套2个(队列)结构体(Queue)——>Queue的结构体在嵌套节点的结构体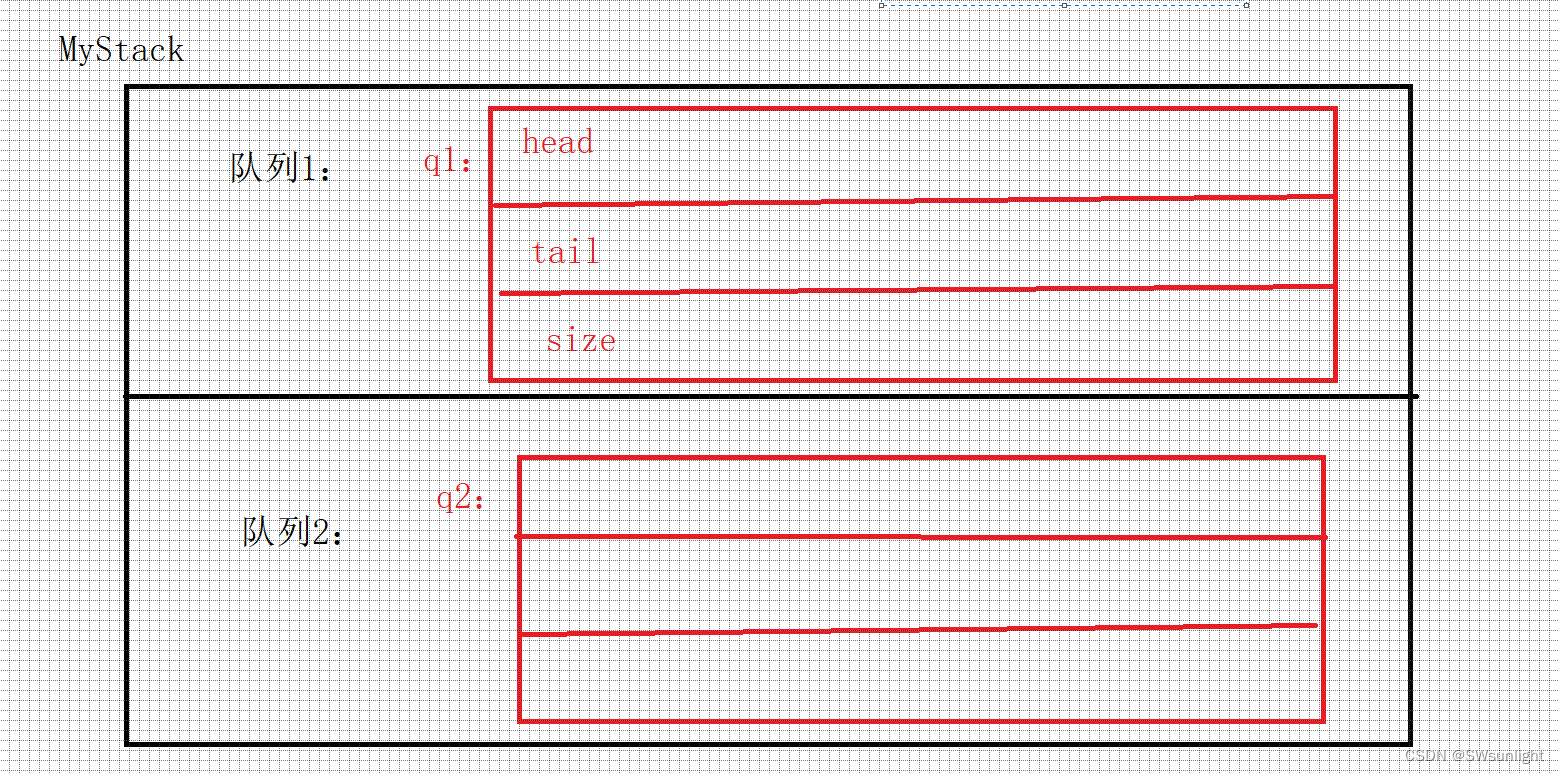
如下:头节点后面还会链接更多的尾节点
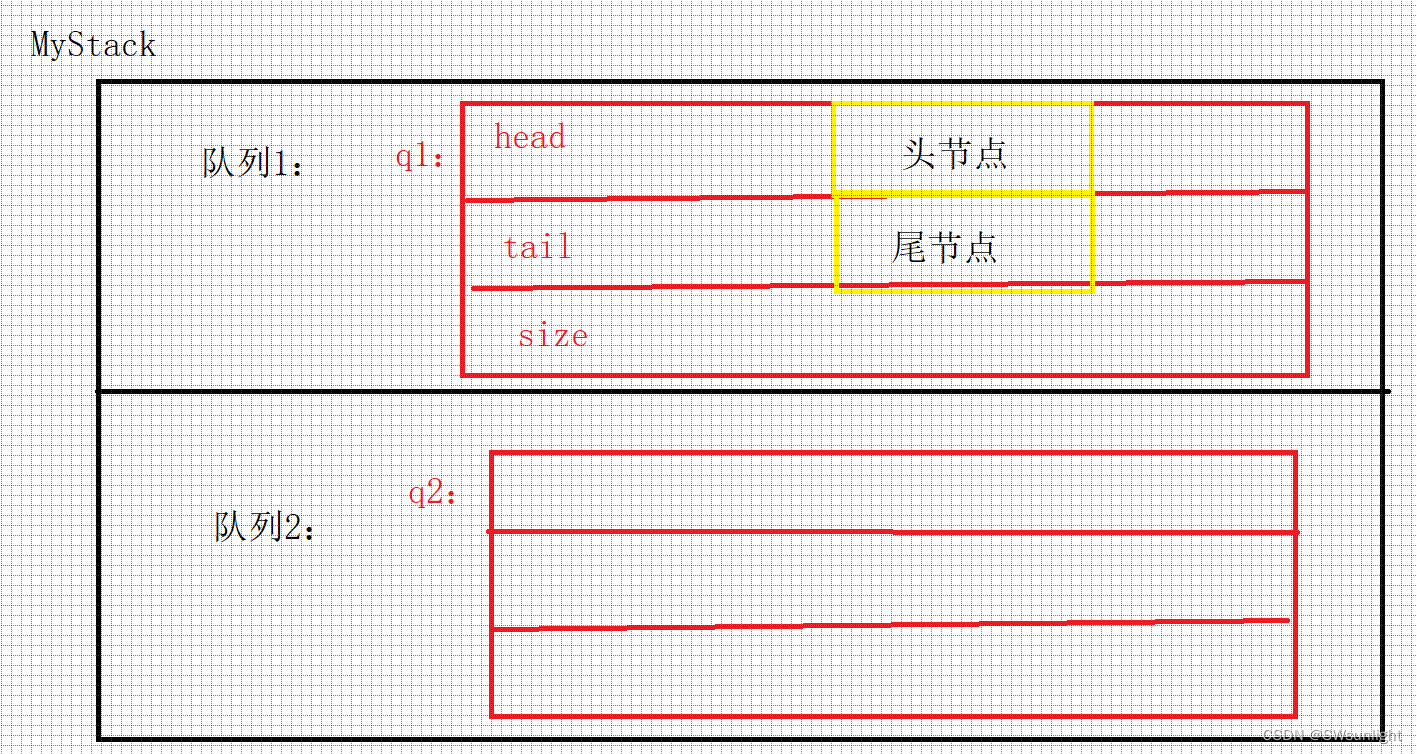
3、代码实现:
将之前写队列的代码复制过来直接可以用了
typedef int QUDataType;
//节点
typedef struct QueueNode{
QUDataType a;
//一定要用指针,不然结构体的大小就无法确定了
struct QueueNode *next;
}QuNode;
//再建立一个保存头和尾的结构体
typedef struct Queue {
QuNode* head;
QuNode* tail;
int size;
}Queue;
//初始化头尾节点
void QuInto(Queue* q)
{
//不能传空指针 即(q=NULL)
assert(q);
q->head = NULL;
q->tail = NULL;
q->size = 0;
}
//尾插(2种情况:1.头尾都为NUL 2.又数据入队列了)
void QuPush(Queue* q, QUDataType x)
{
//申请空间
QuNode* newnode = (QuNode*)malloc(sizeof(QuNode));
//判空
if (newnode == NULL)
{
perror("malloc");
return;
}
newnode->a = x;
newnode->next = NULL;//节点创建完成
//判断尾的位置
if (q->tail == NULL)
{
q->head = q->tail = newnode;
}
else
{
q->tail->next = newnode;
q->tail = newnode;
}
q->size++;
}
//头删(删除到尾以后,就不能再删了)
void QuPop(Queue* q)
{
assert(q);
//头的位置也不能为空
assert(q->size!=0);
//此时数据个数为1(也就是最后一个节点)
if (q->head->next==NULL)
{
free(q->head);
q->head = q->tail = NULL;
}
else//q->head != q->tail;
{
QuNode* next = q->head->next;
free(q->head);
q->head = next;
}
//数据个数也要减去
q->size--;
}
//判空
bool QuEmpty(Queue* q)
{
assert(q);
//头尾都相等时到达同一个位置,此时就为真,其他的情况都为假;
return q->size==0;
}
//取头数据
QUDataType QuFront(Queue* q)
{
assert(q);
assert(q->head);
return q->head->a;
}
//取尾数据
QUDataType QuBack(Queue* q)
{
assert(q);
//队尾都为空了,已经没数据了
assert(q->tail);
return q->tail->a;
}
//数据个数
int QuSize(Queue* q)
{
assert(q);
return q->size;
}
//销毁空间(写进数据,想要一次性释放完就来用)
void QuDestroy(Queue* q)
{
assert(q);
QuNode* cur = q->head;
while (cur)
{
QuNode* next = cur->next;
free(cur);
cur = next;
}
q->head = q->tail =NULL;
q->size = 0;
}
//2个队列
typedef struct {
Queue q1;
Queue q2;
} MyStack;
//初始化
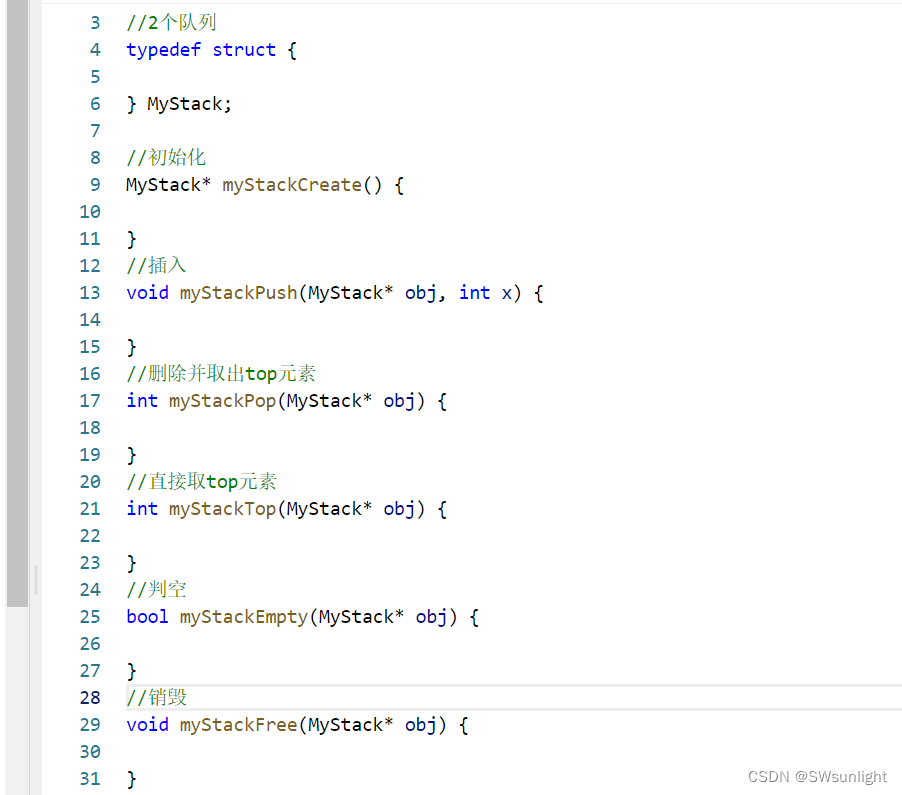
MyStack* myStackCreate() {
MyStack*pts = (MyStack*)malloc(sizeof(MyStack));
if(pts==NULL)
{
perror("malloc");
//exit(1);
return NULL;
}
QuInto(&pts->q1);
QuInto(&pts->q2);
return pts;
}
//插入
void myStackPush(MyStack* obj, int x) {
//判空插入,将数据插入不为空的队列
if(!QuEmpty(&obj->q1))
{
QuPush(&obj->q2,x);
}
else
{
QuPush(&obj->q2,x);
}
}
//删除并取出top元素
int myStackPop(MyStack* obj) {
//假设法:no存不为空
Queue* noEmpty = &obj->q1;
Queue* empty = &obj->q2;
if(!QuEmpty(empty))
{
noEmpty = &obj->q2;
empty = &obj->q1;
}
//我们要让size-1个数据去到那条空通道
while(QuSize(noEmpty)>1)
{
//头删,所以取头
int x = QuFront(noEmpty);
QuPop(noEmpty);
//将其数据存到size-1个数据存入空道
QuPush(empty,x);
}
//随便头还是尾取,因为此时这通道只有最后一个元素了
int top =QuFront(noEmpty);
QuPop(noEmpty);
return top;
}
//直接取top元素
int myStackTop(MyStack* obj) {
//不要删除,只是取元素,那么取不为空的通道的队尾元素(因为根据栈的原则:先出的是队尾元素)
if(!QuEmpty(&obj->q1))
{
return QuBack(&obj->q1);
}
else
{
return QuBack(&obj->q2);
}
}
//判空
bool myStackEmpty(MyStack* obj) {
//2个都是空同通道则为真,否则为假
return QuEmpty(&obj->q1)&&QuEmpty(&obj->q2);
}
//销毁
void myStackFree(MyStack* obj) {
QuDestroy(&obj->q1);
QuDestroy(&obj->q2);
free(obj);
obj = NULL;
}
关于销毁:要先从小(从内向外)的开始,我们应该先从q1和q2进行销毁,在销毁obj
obj申请的空间是为2个队列开辟的,2个队列申请的空间又是为里面的单链表开辟的,你直接销毁大哥,小弟起步就是群龙无首,变成了“野狗”
二、用栈实现队列:
1、题目:
2
2、思路:
和上面思路大差不差
先画图:和上面说的类似,不做赘述
区别1:栈的top指向的是 栈顶元素 还是 栈顶元素下一个位置
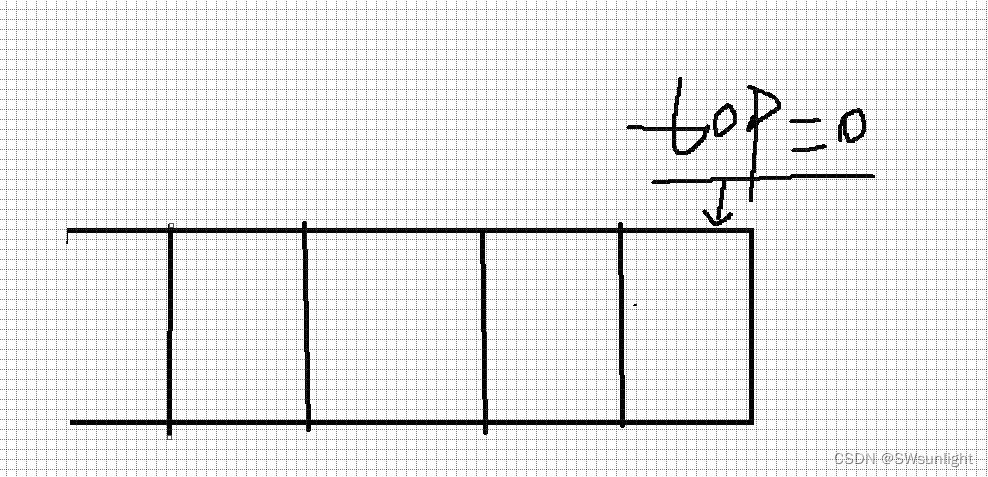
根据之前我写的top指向的是栈顶元素的下一个位置叙说:如下
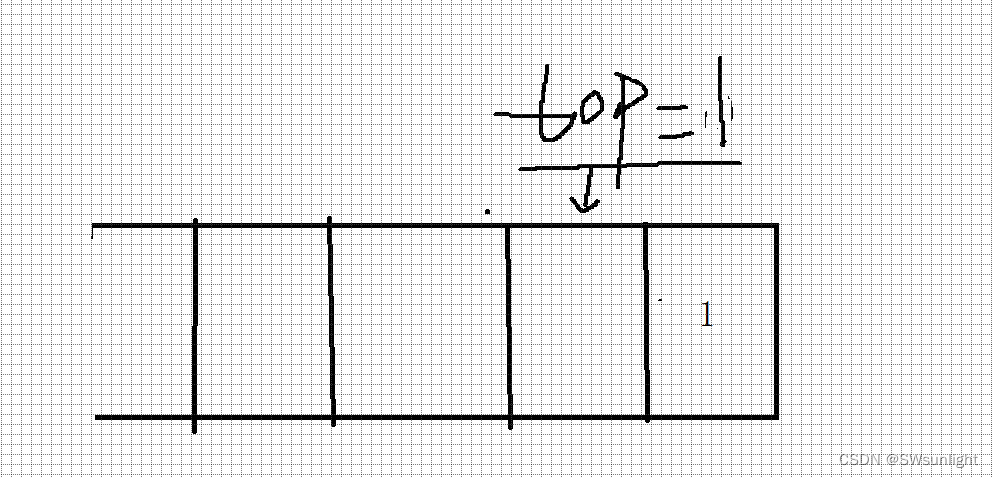
没有数据是top = 0;当存入一个时top = 1;
所以你再取数据放到空的栈时应该也要注意先pop一下再取
还有一个需要注意的点:它比队列实现栈跟倔强(醒悟的更慢)!!!
一个栈里面的数据如下:
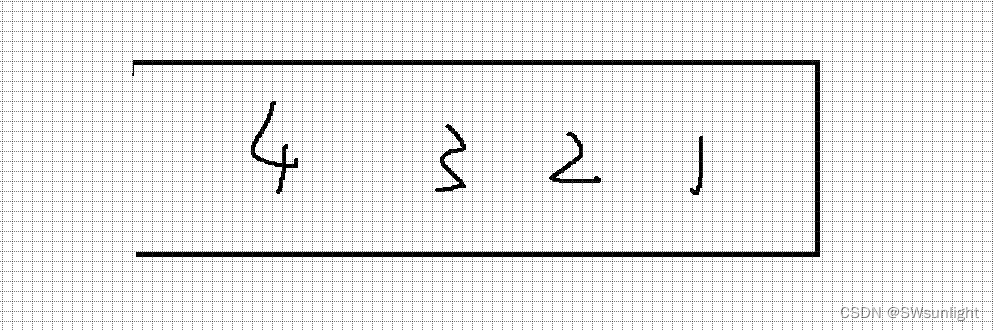
4 3 2 取出放到下面的空栈中
流程图如下:1 就顺利走了,以为这样就完事了??一开始我也这样想的,结果碰壁了
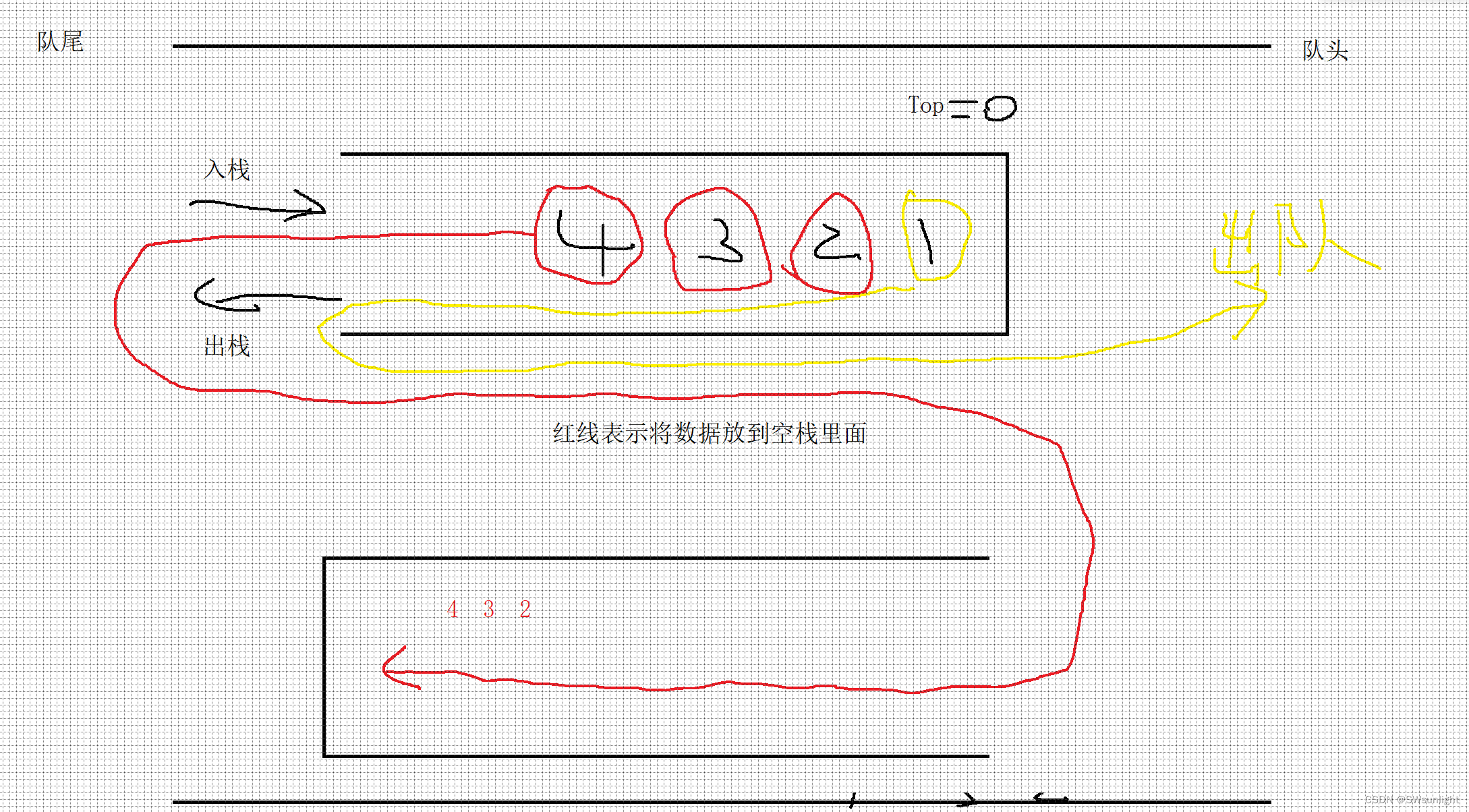
将1取走后,根据之前的思路,再pop时就会将3 2放到上面栈,那么最后出队顺序变成了:1 4 2 3
乱套了
非常不对劲
我想到了再回转一次,这样就可以保证我开始入队时的顺序不变,也就是将上面的栈作为出数据用,每次出一次数据,就将其他数据入栈到下面的栈,出完再回到上面的栈,无论你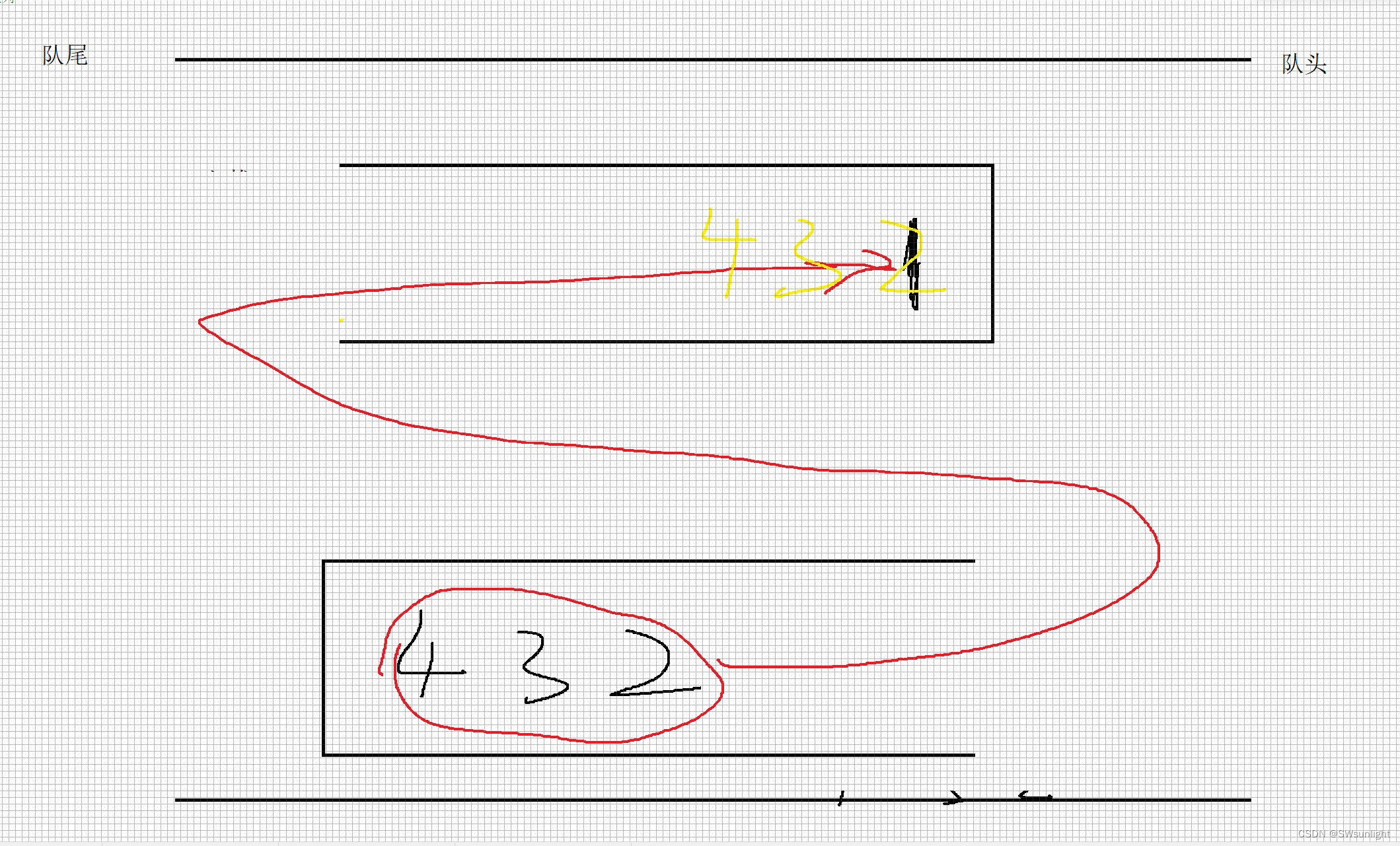
可以理解为:不撞南墙不回头(心死了,才向前)!!!!头比较硬哈,越靠后撞的次数越多
3、代码:
有更好的代码,作参考即可
typedef int LTDataType;
//顺序表(栈)
typedef struct SL
{
LTDataType* a;
int top;
int capacity;
}SL;
//入栈
void SLPush(SL* p,LTDataType x)
{
//不能传NULL,判空;
assert(p);
if (p->top == p->capacity)
{
//先判断是否为0,好进行扩容
int newnode = p->capacity == 0 ? 4 : 2 * (p->capacity);
//扩容;创建一个临时变量接收新的空间,成功在将其交给p->a;
LTDataType* s = (LTDataType*)realloc(p->a,newnode * sizeof(LTDataType));
if (s == NULL)
{
perror("realloc");
return;
}
p->a = s;
p->capacity = newnode;
}
p->a[p->top] = x;
//指向下一个数据地址
p->top++;
}
//出栈(类似尾删)
void SLPop(SL* p)
{
//是否为空
assert(p);
assert(p->top > 0);
p->top--;
}
//初始化
void SLInit(SL* p)
{
p->a = NULL;
p->capacity = 0;
//p->top = -1;//指向栈顶的数据
p->top = 0;//指向栈顶的下一个数据
}
//销毁
void SLDestroy(SL* p)
{
assert(p);
free(p->a);
p->a = NULL;
p->capacity = p->top = 0;
}
//判空
bool SLEmpty(SL* p)
{
//不能是空地址
assert(p);
//为0就是真(true),为1就是假(flase)
return p->top == 0;
}
//数据个数
int SLsize(SL* p)
{
int size = p->top;
return size;
}
//取数据:
LTDataType SLPot(SL*p)
{
assert(p);
return p->a[p->top];
}
//2个栈
typedef struct {
SL q1;
SL q2;
} MyQueue;
//初始化
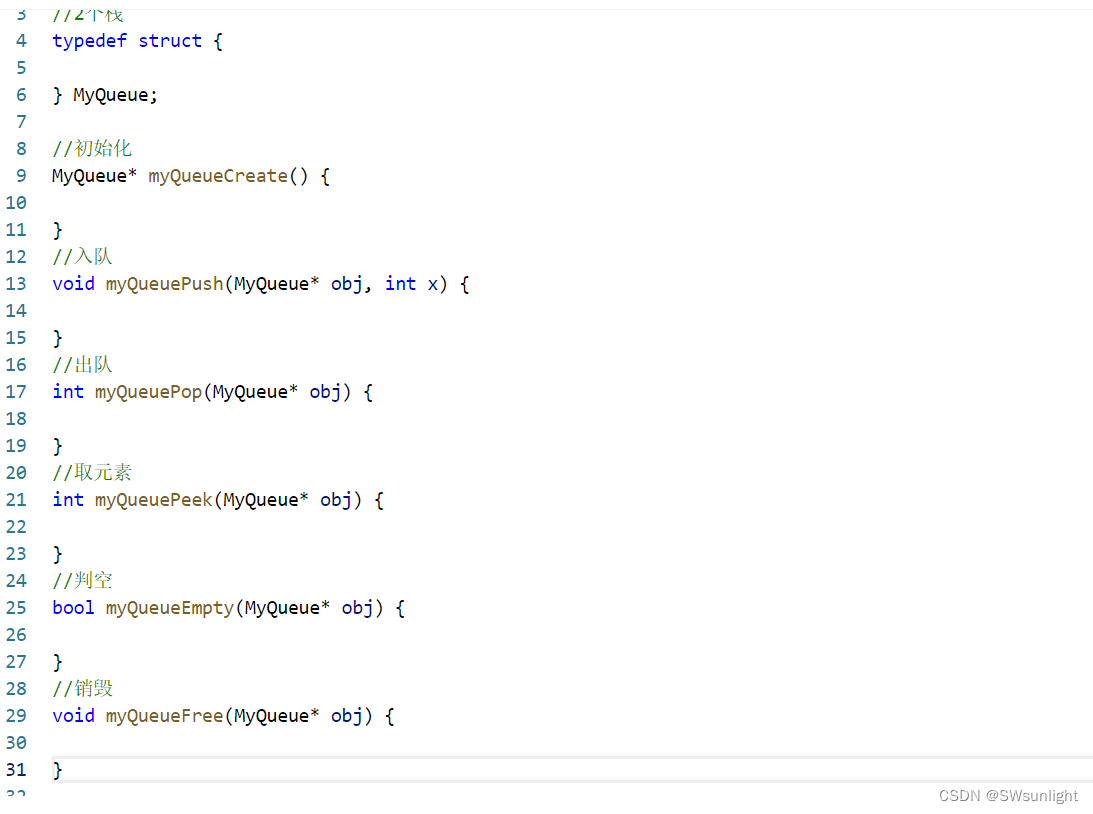
MyQueue* myQueueCreate() {
MyQueue*pts = (MyQueue*)malloc(sizeof(MyQueue));
if(pts==NULL)
{
perror("malloc");
return NULL;
}
SLInit(&pts->q1);
SLInit(&pts->q2);
return pts;
}
//入队
void myQueuePush(MyQueue* obj, int x) {
//非空,存数据:一定要注意top,我的top是指向栈顶元素的下一个位置
if(!SLEmpty(&obj->q1))
{
SLPush(&obj->q1,x);
}
else
{
SLPush(&obj->q2,x);
}
}
//出队
int myQueuePop(MyQueue* obj) {
//假设法:
SL *noEmpty =&obj->q1;
SL *empty =&obj->q2;
if(!SLEmpty(empty))
{
noEmpty =&obj->q2;
empty =&obj->q1;
}
while(SLsize(noEmpty)>1)
{
//根据top指向位置要先pop
SLPop(noEmpty);
int x = SLPot(noEmpty);
SLPush(empty,x);
}
SLPop(noEmpty);
int Top = SLPot(noEmpty);
while(!SLEmpty(empty))
{
//根据top指向位置要先pop
SLPop(empty);
int x = SLPot(empty);
SLPush(noEmpty,x);
}
return Top;
}
//取
int myQueuePeek(MyQueue* obj) {
SL*qq1 = &obj->q1;
SL*qq2 = &obj->q2;
//直接取第一个进去的数据
if(!SLEmpty(qq1))
{
return qq1->a[0];
}
else
{
return qq2->a[0];
}
}
//判空
bool myQueueEmpty(MyQueue* obj) {
return SLEmpty(&obj->q1)&&SLEmpty(&obj->q2);
}
//销毁
void myQueueFree(MyQueue* obj) {
SLDestroy(&obj->q1);
SLDestroy(&obj->q2);
free(obj);
obj = NULL;
}三、设计循环队列:
粗略讲解一下:循环队列
循环队列是一种线性数据结构。它也被称为“环形缓冲器”,大致就是一个队列有了空间大小,这个空间只能存出的数据是有限个,满了不能存,未满则可以继续存,相当于苍蝇馆吃饭,比较火爆,只能坐下k个人,那么就得排队,若是离开一个,就能进去一个,接着走
1、题目:

2、思路:
有链表和顺序表(数组)都可以实现,我用的数组,因为更简单一点:
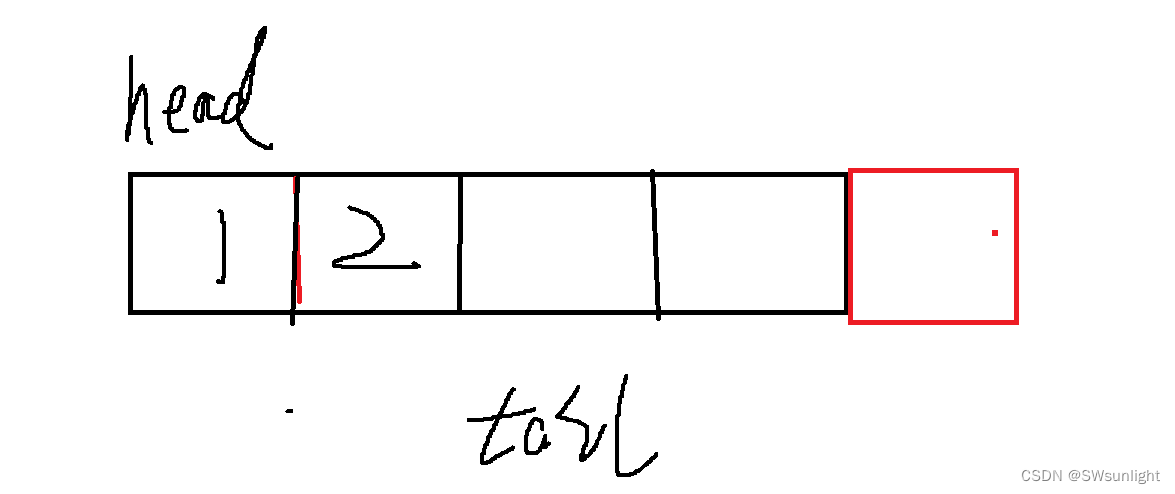
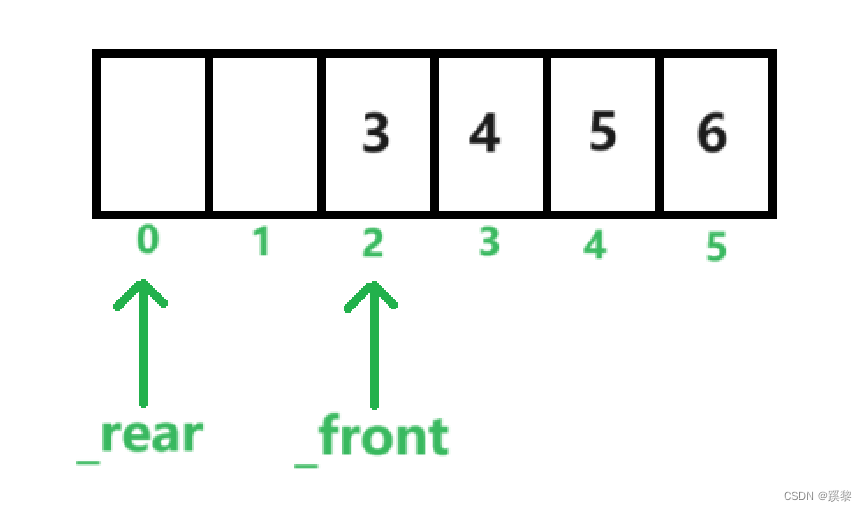
根据上面的介绍可以知道,循环列队要一个标记首和尾的变量(head和tail)
初状态:都在头的位置,下标来看的话就是 0 的位置
检查队列满和空的情况:
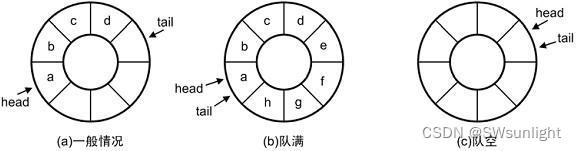
空的情况:很简单,就是head = tail
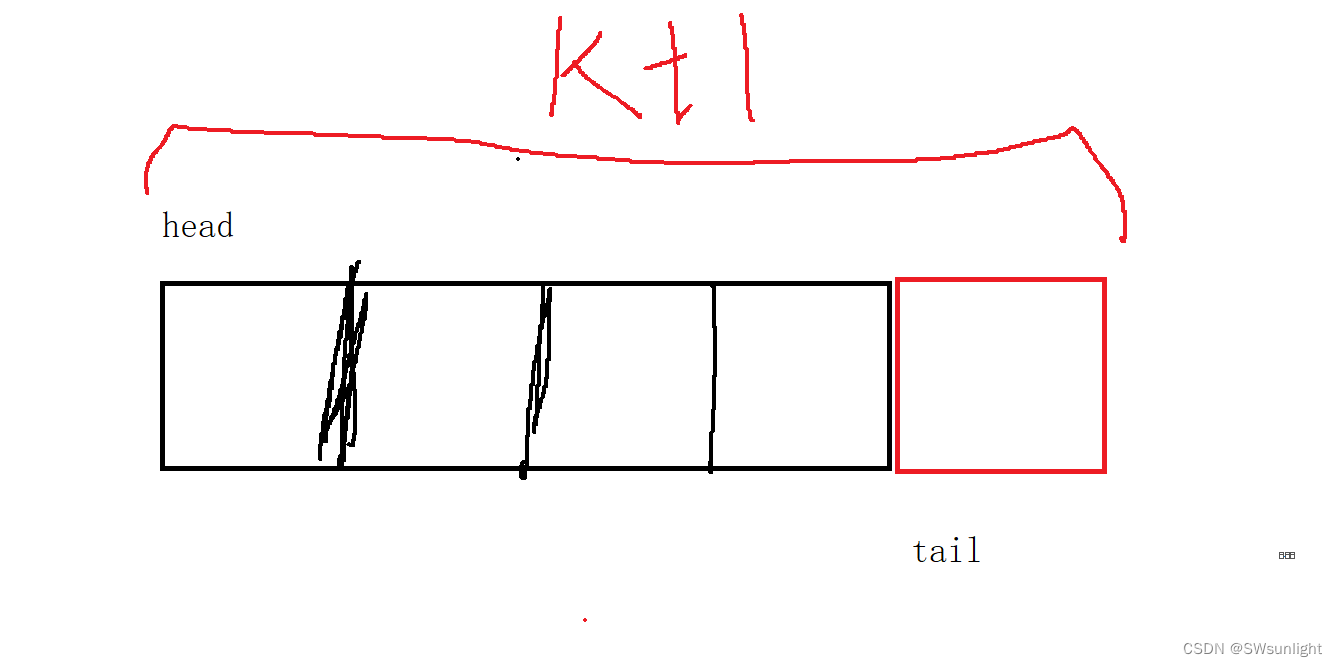
满队时,tail应该指向的下一个位置,存一个数据tail后移一位,所以如下:4个数据的空间,满队时,刚好 tail = k(k表示数据个数(空间大小))要判满的话 也是tail==head才行,
tail%k==head; 但是这么做的话有问题:空也是head == tail,这不是冲突么!
有2种方法:任选,操作难度差不多
1、设置size ——记下数据个数
2、多创建一个空间
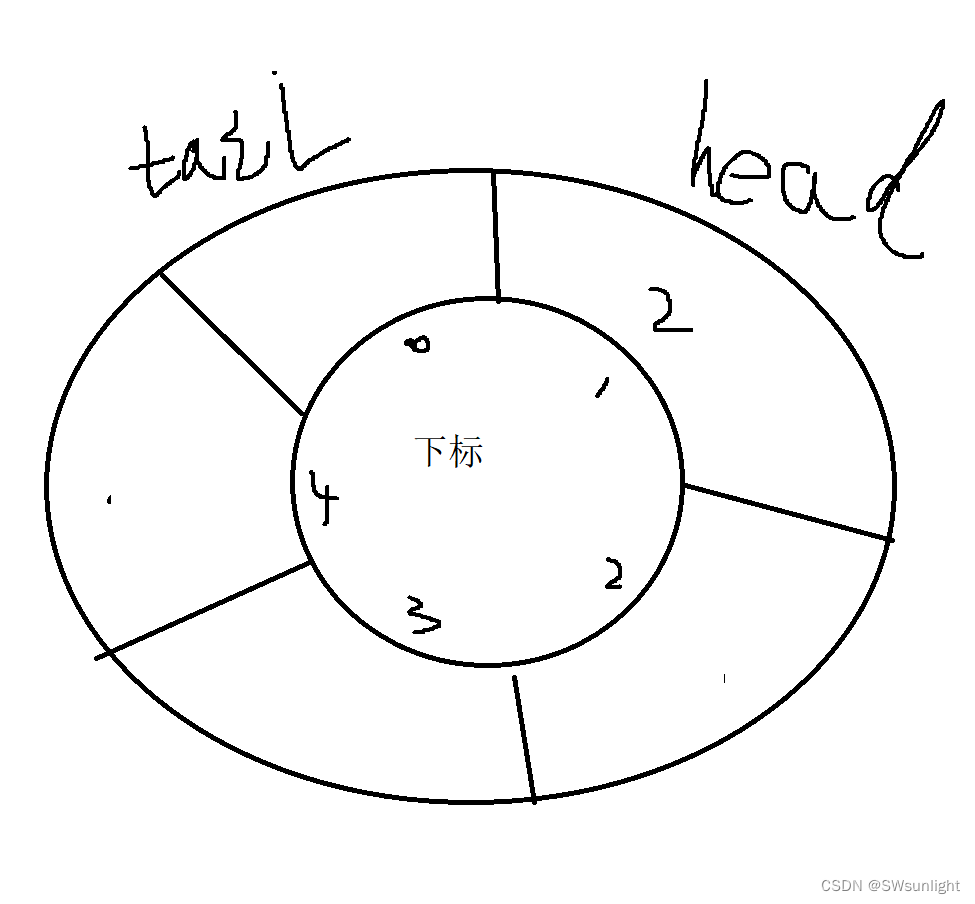
当满栈时,tail与head差了一步,我们写下 (tail+1)%(k+1);有点抽象,看下面
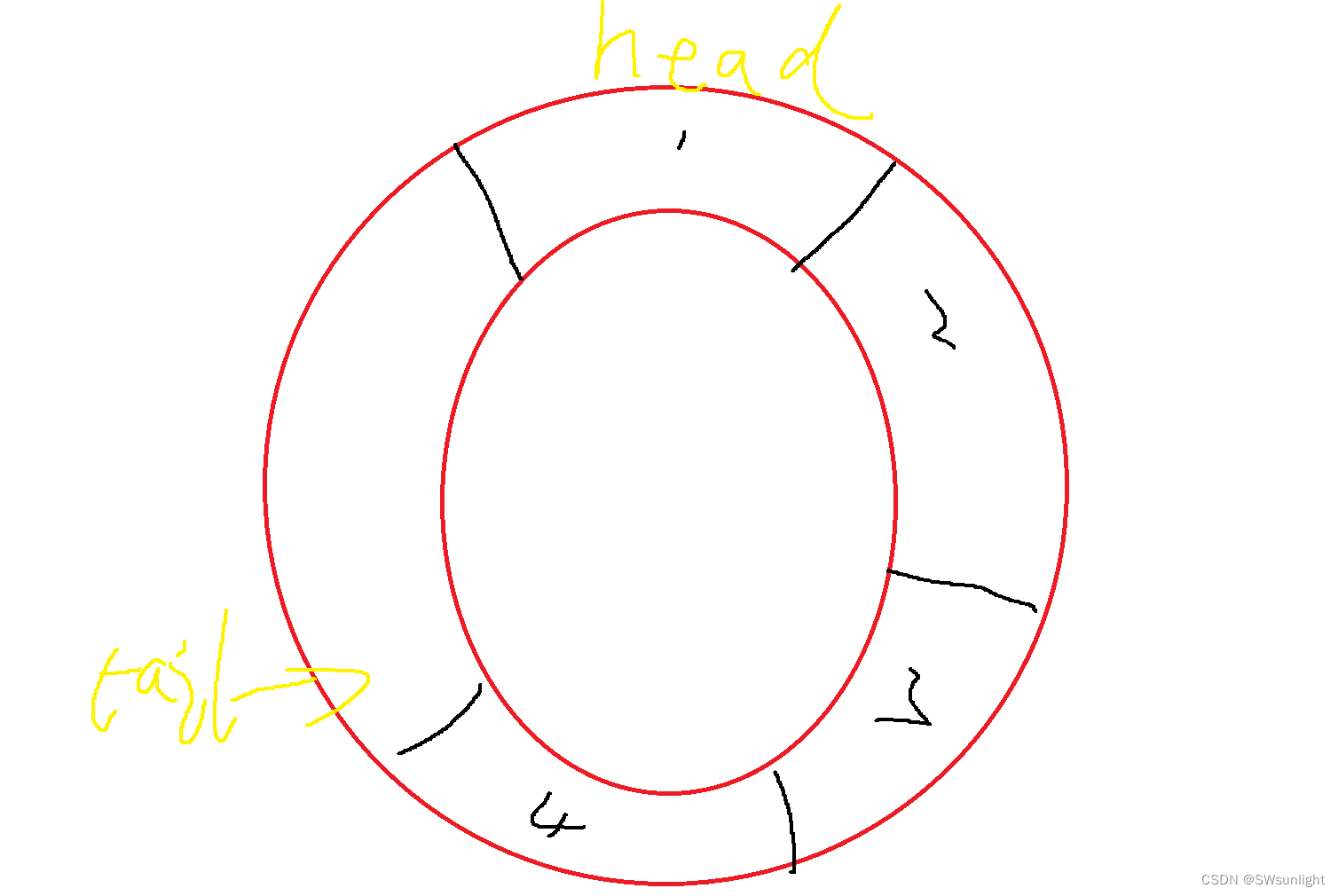
给它用环来看:是不是更清晰了,头和尾的差了一个 1也就是tail+1;因为数组是一块连续的空间,所以我们要用%(k+1)将尾和头相连
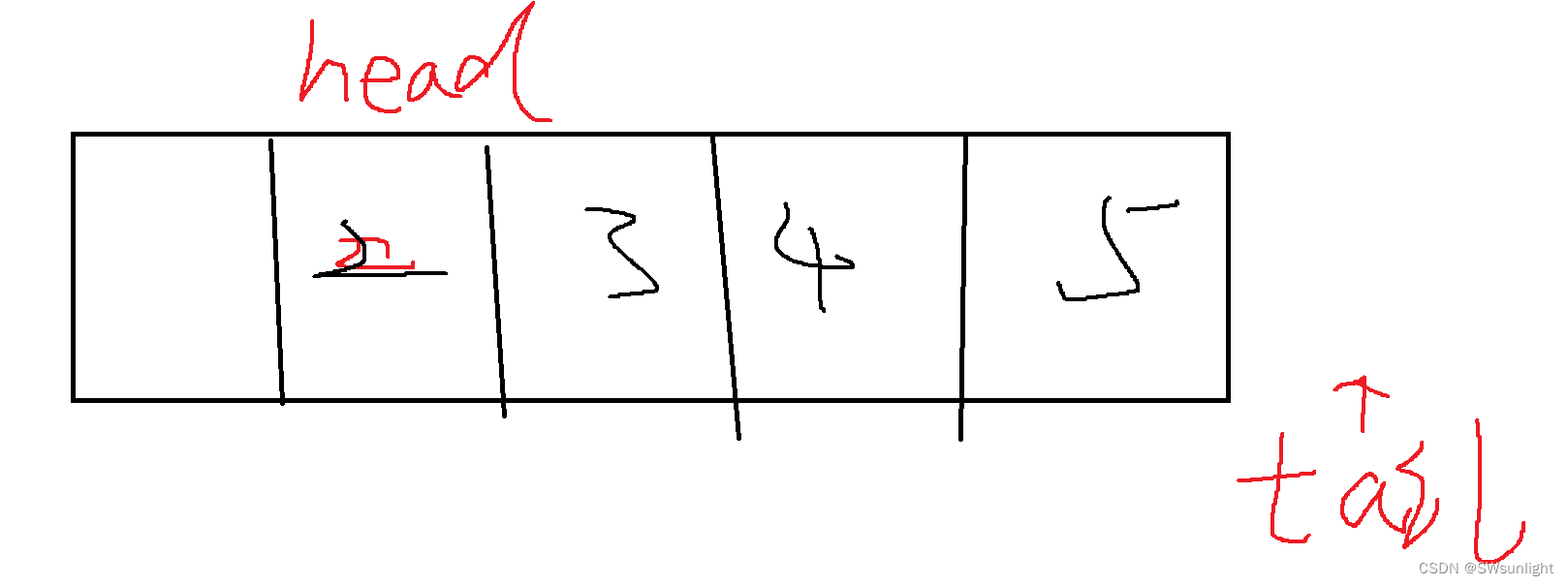
插入数据时,需要注意tail的取值:
先存数据再给tail = tail+1;但是tail不能一直往后走的(循环规定了循环的范围)!!!!它的取值只能是[0,k];所以要写一个tail %=(k+1); 因为x%k (取值为:0 —— k-1)
若是数据如此:tail是在下标为5的位置,后面是不能用的,所以要将tail传回到头去,保证了差一步(保证了一个空间不能用,因为我们多申请了一个,这个空间只是饰品,不能用)
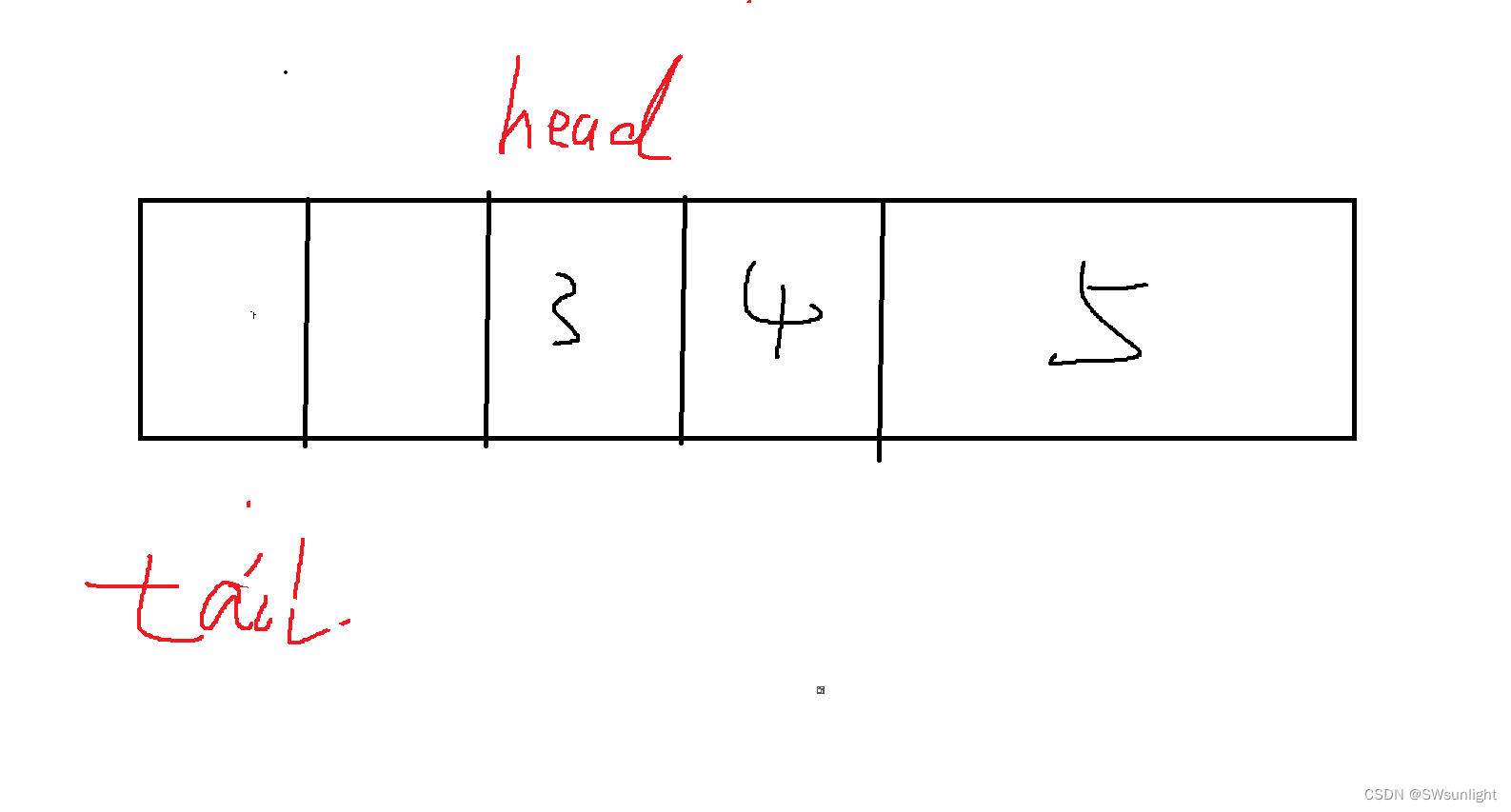
取尾元素:
tail的位置是下一个元素的位置,所以要用tail-1来调用,但是有坑,当tail的位置到达了下标0处,还能减掉吗???那不就是-1么,但是我们要的取的值tail-1的范围应该是[o,k]这个区间范围内
上面我们是 tail = tail%(k+1);——>>> tail-1 = tail%(k+1)-1;
我们要将它区间变成[0,k]; 变形:
3、代码:
typedef struct {
int *a;
int head;
int tail;
int k;
} MyCircularQueue;
//因为在判空和判满的上面的函数需要调用他俩,所以我们要进行函数声明
bool myCircularQueueIsFull(MyCircularQueue* obj);
bool myCircularQueueIsEmpty(MyCircularQueue* obj);
//初始化:
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue*pts = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
if(pts==NULL)
{
perror("malloc");
return NULL;
}
pts->a = (int*)malloc(sizeof(int)*(k+1));
if(pts->a==NULL)
{
perror("malloc");
return NULL;
}
pts->k = k;
pts->tail = pts->head =0;
return pts;
}
//插入,返回真假
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
//是否为满,满了就不能插入;
if(myCircularQueueIsFull(obj))
{
return false;
}
else
{
obj->a[obj->tail]= value;
obj->tail++;
obj->tail%=(obj->k+1);
return true;
}
}
//删除:返回真假
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
//是否为空,为空不能删除
if(myCircularQueueIsEmpty(obj))
{
return false;
}
else
{
obj->head++;
obj->head%=(obj->k+1);
return true;
}
}
//取头元素
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[obj->head];
}
}
//取尾元素
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[(obj->tail-1+obj->k+1)%(obj->k+1)];
}
}
//s是否为空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head == obj->tail;
}
//是否满
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return obj->head == (obj->tail+1)%(obj->k+1);
}
//销毁
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
obj->a =NULL;
free(obj);
obj = NULL;
}


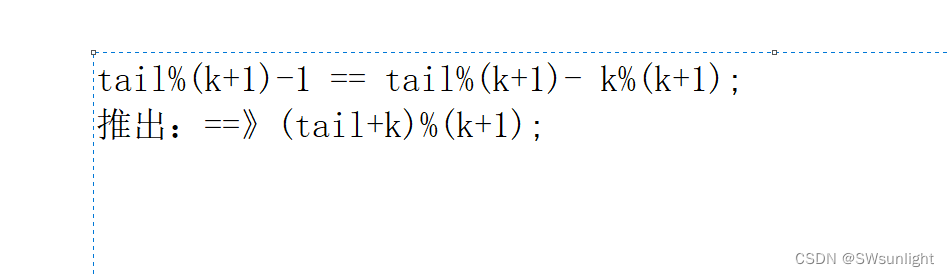






![[AutoSar]BSW_Com021单帧 首帧 流控帧 连续帧 详解](https://img-blog.csdnimg.cn/direct/9741b74f351340cc919265c8db329110.png)