题干：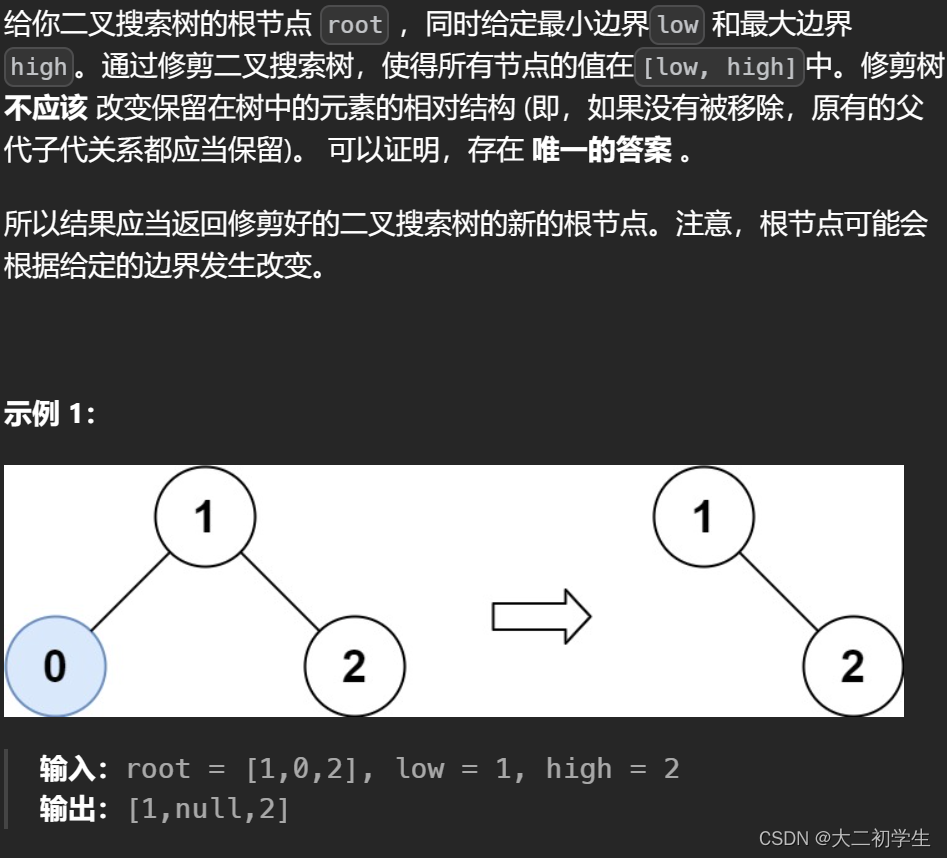

代码：

class Solution {
public:
    TreeNode* traversal(TreeNode* root, int low, int high){
        if(root == NULL)return  NULL;
        if(root->val < low)return traversal(root->right, low, high);
        if(root->val > high)return traversal(root->left, low, high);
        root->left = traversal(root->left, low, high);
        root->right = traversal(root->right, low, high);
        return root;
    }
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == NULL)return NULL;
        return traversal(root, low, high);
    }
};

要点：修剪操作的触发条件时节点值在区间之外，小于low大于high。但虽然根节点值小于low可是由于BST的特性其比根节点值大的右子树可能会大于low，所以需要将其右子树也加入递归进行判断，并且将结果返回给上一层。然后创建root->right = traversal(root->right,low,high）来接收返回值。