在 Mac 上删除的文件将被移至垃圾箱并保留 30 天,然后才会被永久删除。然而,许多 Mac 用户可能会意外清空垃圾箱,而没有意识到其中包含重要文件。本指南包含从清空的废纸篓中恢复 Mac 上已删除文件的所有有效方法。
当您意识到自己不小心清空了 Mac 上的垃圾箱时,请迅速采取行动并停止使用它;继续使用它会使重要文件面临被新数据覆盖的风险,从而使它们几乎无法恢复。
方法 1:使用数据恢复软件恢复 Mac 上清空的废纸篓
使用数据恢复程序是清空垃圾箱后恢复已删除文件的最快方法。奇客数据恢复Mac版是最好的数据恢复软件之一,具有用户友好的界面来执行 Mac 垃圾恢复。
使用 奇客数据恢复Mac版 工具,您可以恢复意外清空Mac上垃圾箱后永久删除的文件,包括照片、文档、视频、档案等。
奇客数据恢复: 支持1000+数据格式恢复免费下载软件扫描数据,支持文件、照片、视频、邮件、音频等1000+种文件的格式恢复更有电脑/笔记本、回收站、U盘、硬盘等各类存储设备数据丢失恢复![]() https://www.geekersoft.cn/geekersoft-data-recovery.html
https://www.geekersoft.cn/geekersoft-data-recovery.html
请按照以下步骤使用数据恢复软件恢复 Mac 上清空的废纸篓:
第 1 步:扫描丢失和删除的文件
启动适用于 Mac 的 奇客数据恢复Mac版 ,然后选择磁盘或垃圾箱文件夹中的其他磁盘。单击“搜索丢失的文件”。

第 2 步:找到被删除的文件
快速深度扫描后,将显示清空的垃圾箱文件夹中已删除的文件。这款强大的数据恢复软件提供过滤功能,帮助您快速找到所需的可恢复文件。
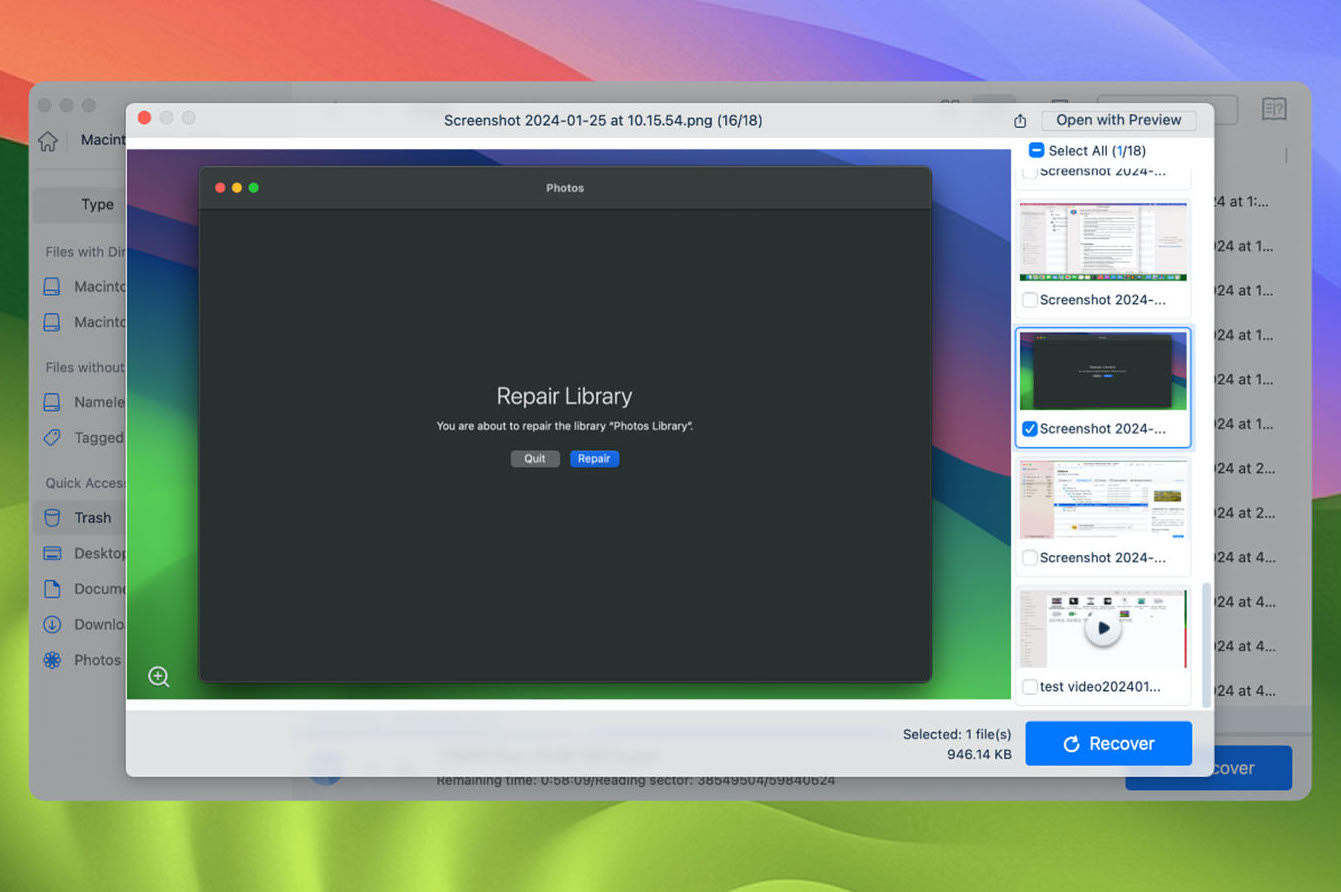
步骤 3:预览并恢复已删除的文件
如果您需要帮助确定需要哪个已删除的文件,请单击眼睛图标预览文件内容。然后单击“恢复”或“全部恢复”按钮从清空的废纸篓中恢复已删除的文件。
有时,您仍然可以在没有软件的情况下恢复清空的垃圾箱。查看以下三种在 Mac 上恢复垃圾箱的方法。
方法 2:从 Time Machine 备份恢复 Mac 上意外清空的废纸篓
macOS 提供了强大的 Time Machine 程序。它可以将您的 Mac 恢复到特定时间,包括其设置和数据。如果您在时间机器中备份了已删除的文件,则可以在清空垃圾箱后恢复它们。以下是您可以参考的步骤:
第 1 步:将 Time Machine 备份磁盘连接到 Mac。
步骤 2:单击顶部菜单中的 Time Machine 图标,然后选择“浏览 Time Machine 备份”选项。
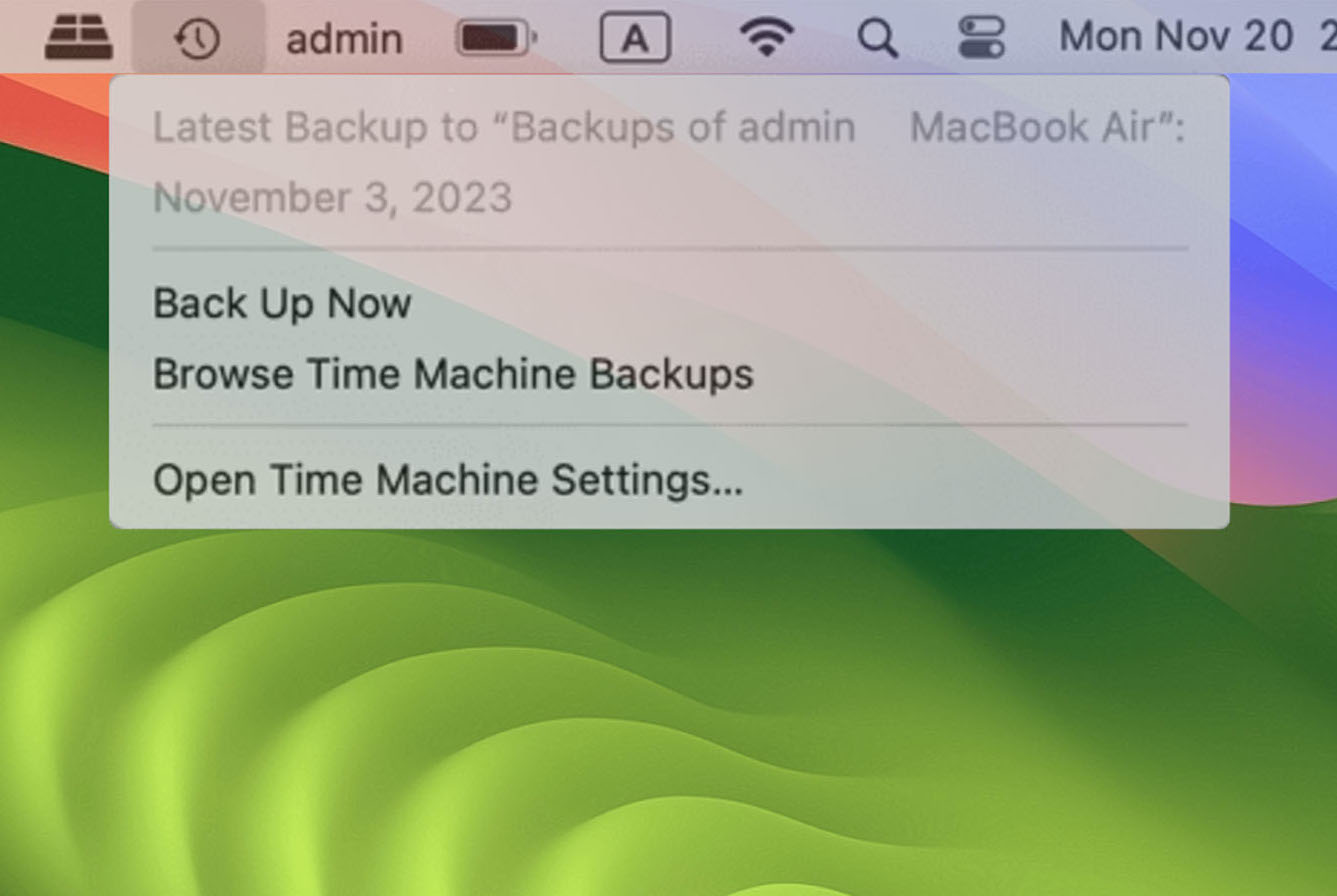
第三步:在原来的位置搜索你想要的文件;按时间和日期过滤文件的版本,然后单击“恢复”将它们恢复到您的 Mac 上。
方法 3:使用 iCloud 备份清空 Mac 上的垃圾箱后恢复已删除的文件
除了使用Time Machine备份数据外,iCloud还提供便捷的云备份服务;一旦你在Mac上打开iCloud同步,Mac删除的文件就可以通过iCloud备份找回。值得注意的是,这种方法也有30天的时间限制。
请查看以下步骤,使用 iCloud 备份恢复 Mac 上清空的废纸篓:
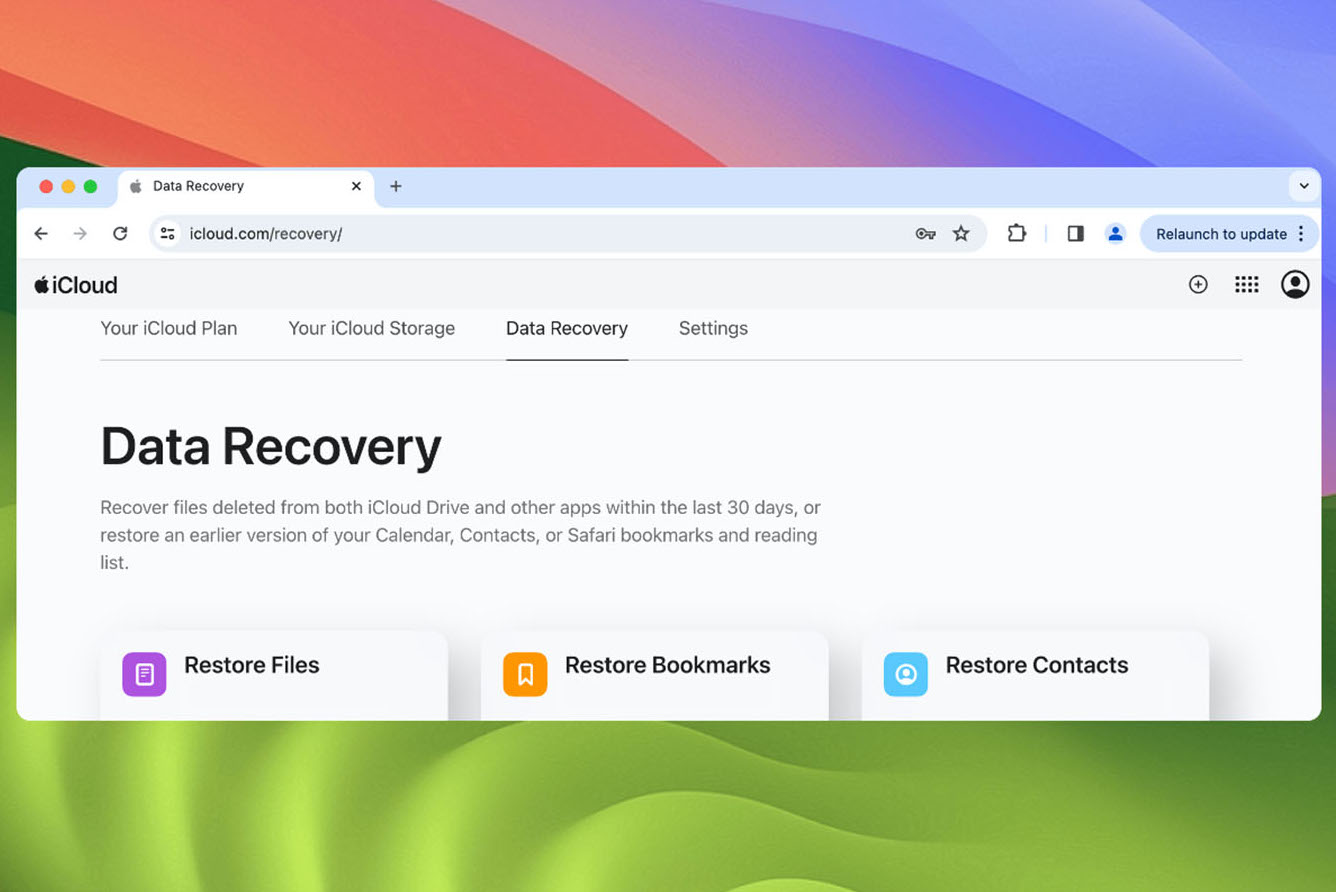
第 1 步:访问iCloud 并使用您的 Apple ID 登录。
步骤2:选择“数据恢复”选项,然后等待网站在您的iCloud帐户中搜索可恢复的文件。
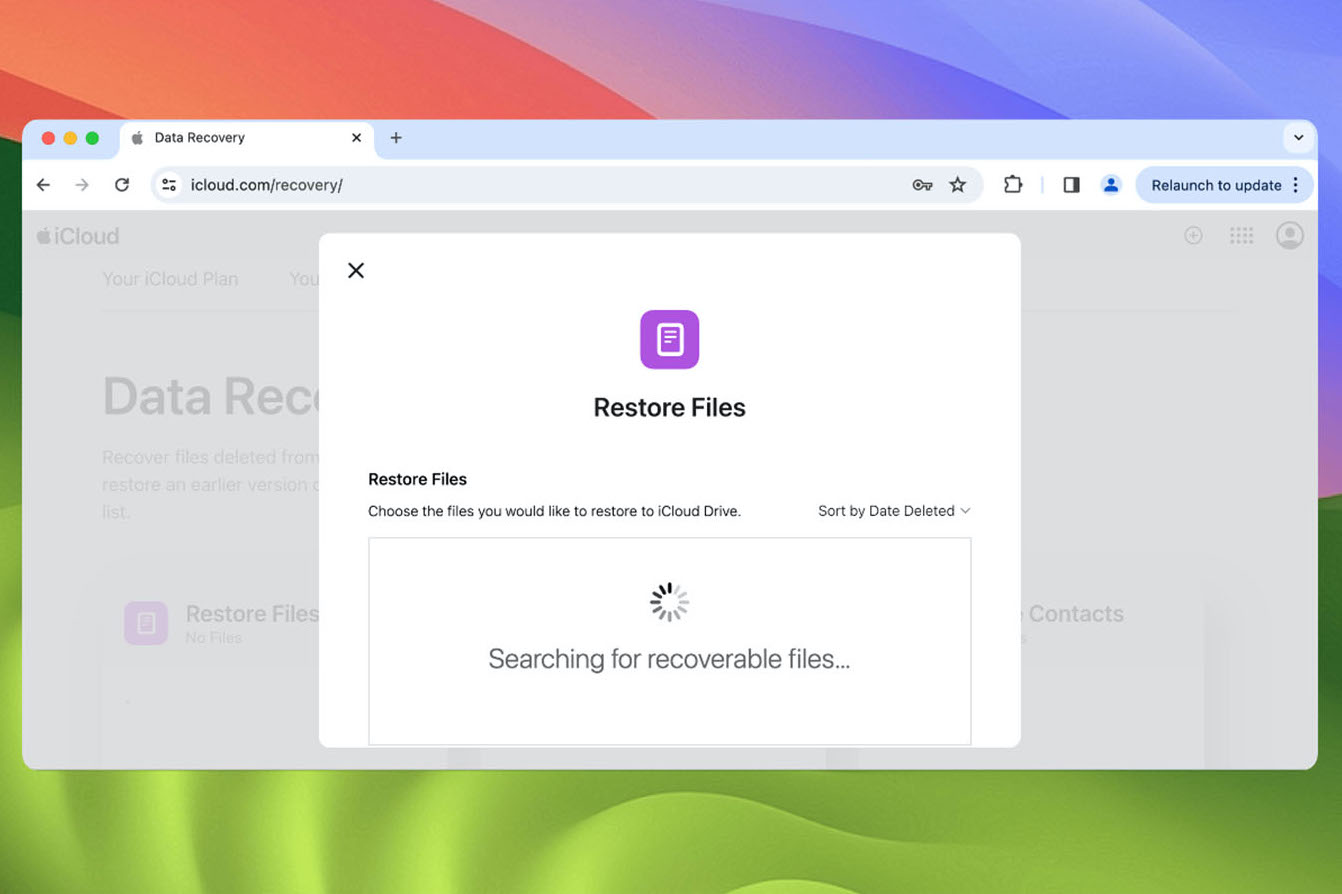
第三步:找到需要恢复的文件,勾选文件前面的复选框将其选中,然后单击“恢复文件”进行保存。
注意: iCloud 备份有限的文件类型,包括照片、视频、联系人、日历、笔记、iWork 文档和电子邮件。
方法 4:使用终端从 Mac 上清空的废纸篓中恢复文件
终端是 Mac 上的内置程序,就像 Windows 计算机上的命令提示符一样,它允许用户使用命令行执行不同的任务,例如从 Mac 垃圾箱中恢复已删除的文件。
但坦率地说,如果清空 Trash,则很难通过命令行从清空的 Trash 文件夹中检索已删除的文件。您可以尝试这种有用的命令行方式来恢复已删除的垃圾文件。
以下是如何使用终端程序在 Mac 上恢复清空的废纸篓:
步骤 1:从“Finder > 应用程序 > 实用程序 > 终端”路径启动终端。
步骤 2:输入cd。垃圾桶并按 Enter 键。然后,输入mv xxx,将“xxx”替换为已删除文件的名称,然后再次按 Enter 键。
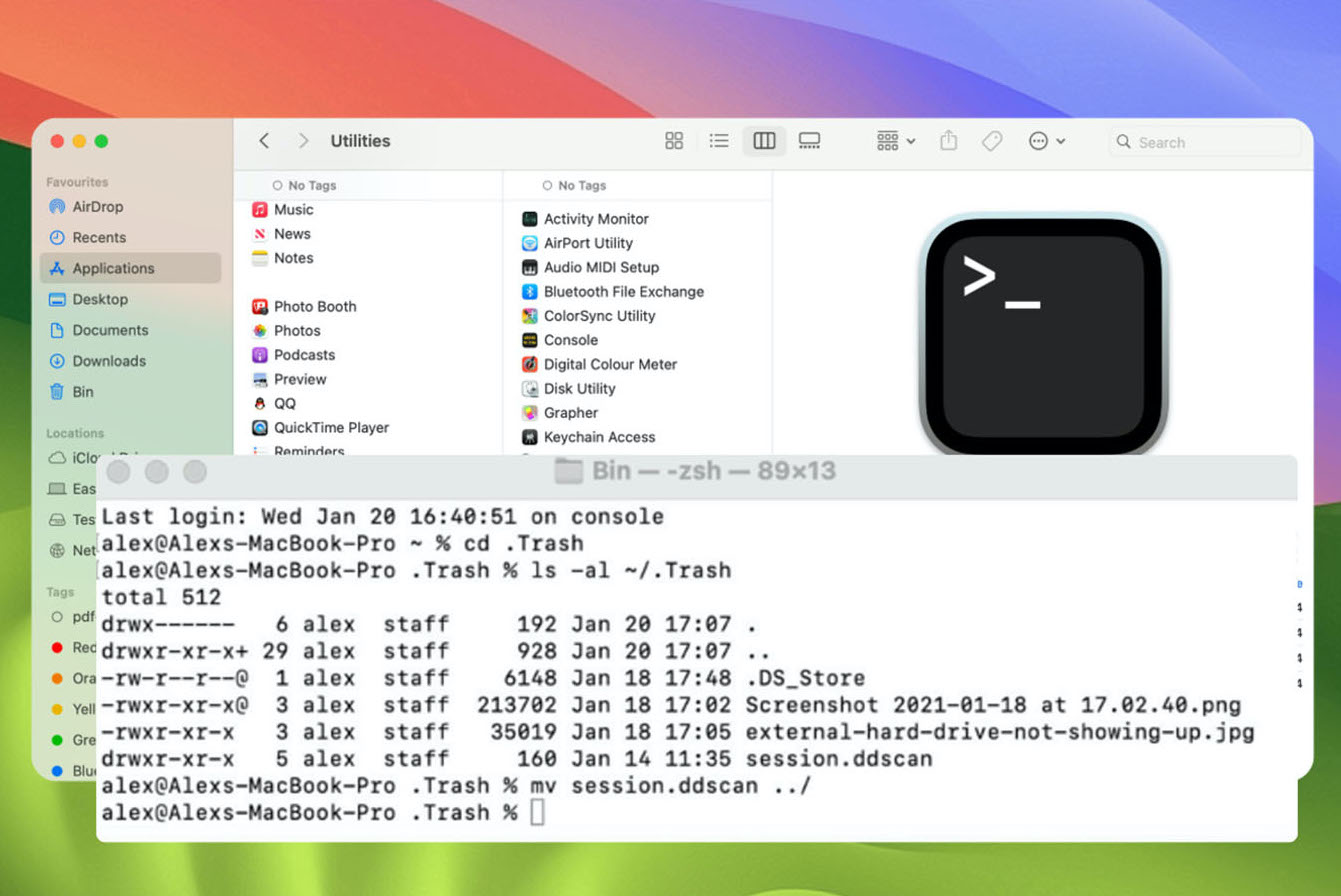
步骤 3:输入Quit以关闭终端。启动“Finder”,在窗口右上角的搜索栏中输入已删除文件的名称即可找到恢复的文件。
Mac 垃圾恢复常见问题解答
以下是有关 Mac 垃圾恢复的常见问题:
清空废纸篓会永久删除 Mac 上的文件吗?
清空废纸篓并不意味着永久删除 Mac 上的文件,您可以使用数据恢复软件(例如专业且值得信赖的 奇客数据恢复mac版)从清空的废纸篓中恢复已删除的文件。
Mac 清空回收站后可以恢复已删除的文件吗?
只要新数据不会覆盖已删除的数据,您就可以在清空 Mac 上的回收站后恢复已删除的文件。查看以下步骤:
步骤 1:安装并启动奇客数据恢复mac版。
步骤2:选择要扫描可恢复数据的目标磁盘。
步骤 3:扫描过程完成后,预览并恢复 Mac 上清空回收站中已删除的文件。
如何恢复 Mac 上已清空的垃圾箱中已删除的文件?
您可以通过以下方法从清空的垃圾箱中免费恢复 Mac 上已删除的文件:
- 使用 Time Machine 备份从清空的废纸篓中恢复 Mac 上已删除的文件
- 使用 iCloud 备份清空垃圾箱后恢复 Mac 上的文件
- 使用 奇客数据恢复mac版免费版从清空的垃圾箱中恢复已删除的文件
如何在没有软件的情况下从 Mac 垃圾箱中恢复已删除的文件?
您可以通过从 Time Machine 或 iCloud 备份恢复已删除的文件,无需软件即可从 Mac 上的“废纸篓”中恢复这些文件。但是从备份恢复已删除的文件有一个明显的限制:在删除文件之前必须先备份它们。否则,您必须考虑使用软件或向数据恢复服务寻求帮助。
结论
在不确定垃圾箱中是否有重要文件的情况下清空垃圾箱可能会导致严重的数据丢失,并对您的工作和生活造成巨大打击。但不要惊慌。本文讨论了专业的数据恢复工具和清空垃圾箱后恢复已删除文件的有效方法。
您可以选择合适的方法来执行 Mac 垃圾恢复并通过分步指南返回您的宝贵数据。






![[muduo网络库]——muduo库三大核心组件之 Poller/EpollPoller类(剖析muduo网络库核心部分、设计思想)](https://img-blog.csdnimg.cn/direct/c835e66dd7f3493e94b40369c641205e.png)