文章目录
- 题目:Dijkstra求最短路
- 思路
- 伪代码:
- 代码
- 优化
- 优化代码:
- Java代码
- 总结
题目:Dijkstra求最短路
给定一个 n个点 m条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1号点到 n号点的最短距离,如果无法从 1号点走到 n号点,则输出 −1。
输入格式
第一行包含整数 n和 m。
接下来 m行每行包含三个整数 x,y,z,表示存在一条从点 x到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1号点到 n号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1 ≤ n ≤ 500,1 ≤ m ≤ 105,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
思路
迪杰斯特拉算法采用的是一种贪心的策略。
求源点到其余各点的最短距离步骤如下:
-
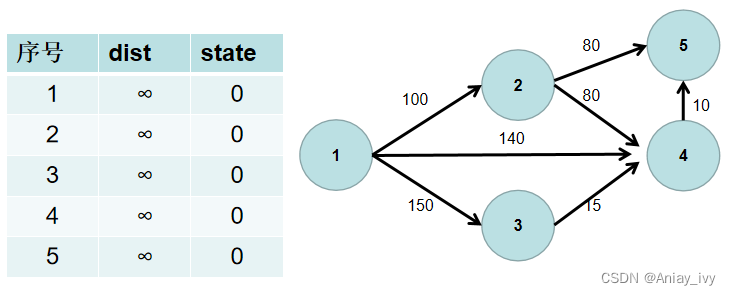
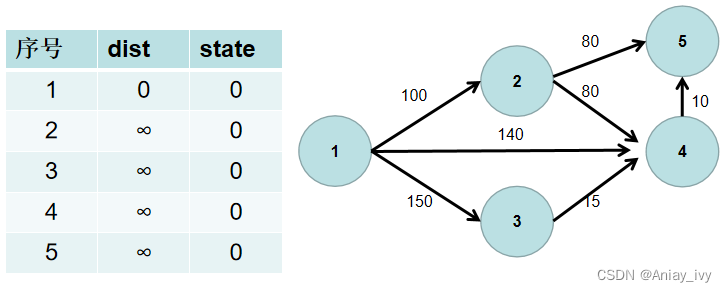
用一个 dist 数组保存源点到其余各个节点的距离,dist[i] 表示源点到节点 i 的距离。初始时,dist 数组的各个元素为无穷大。
用一个状态数组 state 记录是否找到了源点到该节点的最短距离,state[i] 如果为真,则表示找到了源点到节点 i 的最短距离,state[i] 如果为假,则表示源点到节点 i 的最短距离还没有找到。初始时,state 各个元素为假。
-
源点到源点的距离为 0。即dist[1] = 0。
-
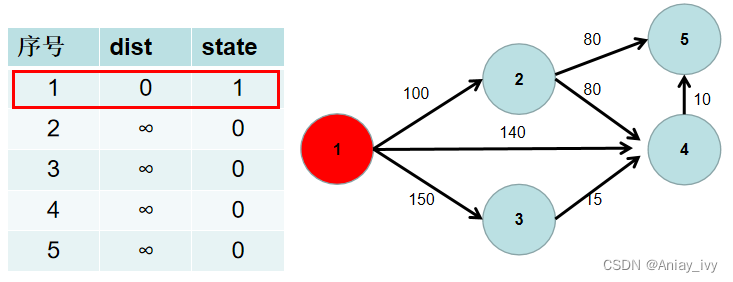
遍历 dist 数组,找到一个节点,这个节点是:没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 i。此时就找到了源点到该节点的最短距离,state[i] 置为 1。
-
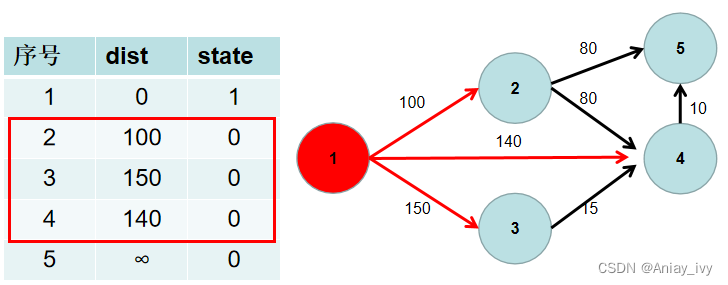
遍历 i 所有可以到达的节点 j,如果 dist[j] 大于 dist[i] 加上 i -> j 的距离,即 dist[j] > dist[i] + w[i][j](w[i][j] 为 i -> j 的距离) ,则更新 dist[j] = dist[i] + w[i][j]。
-
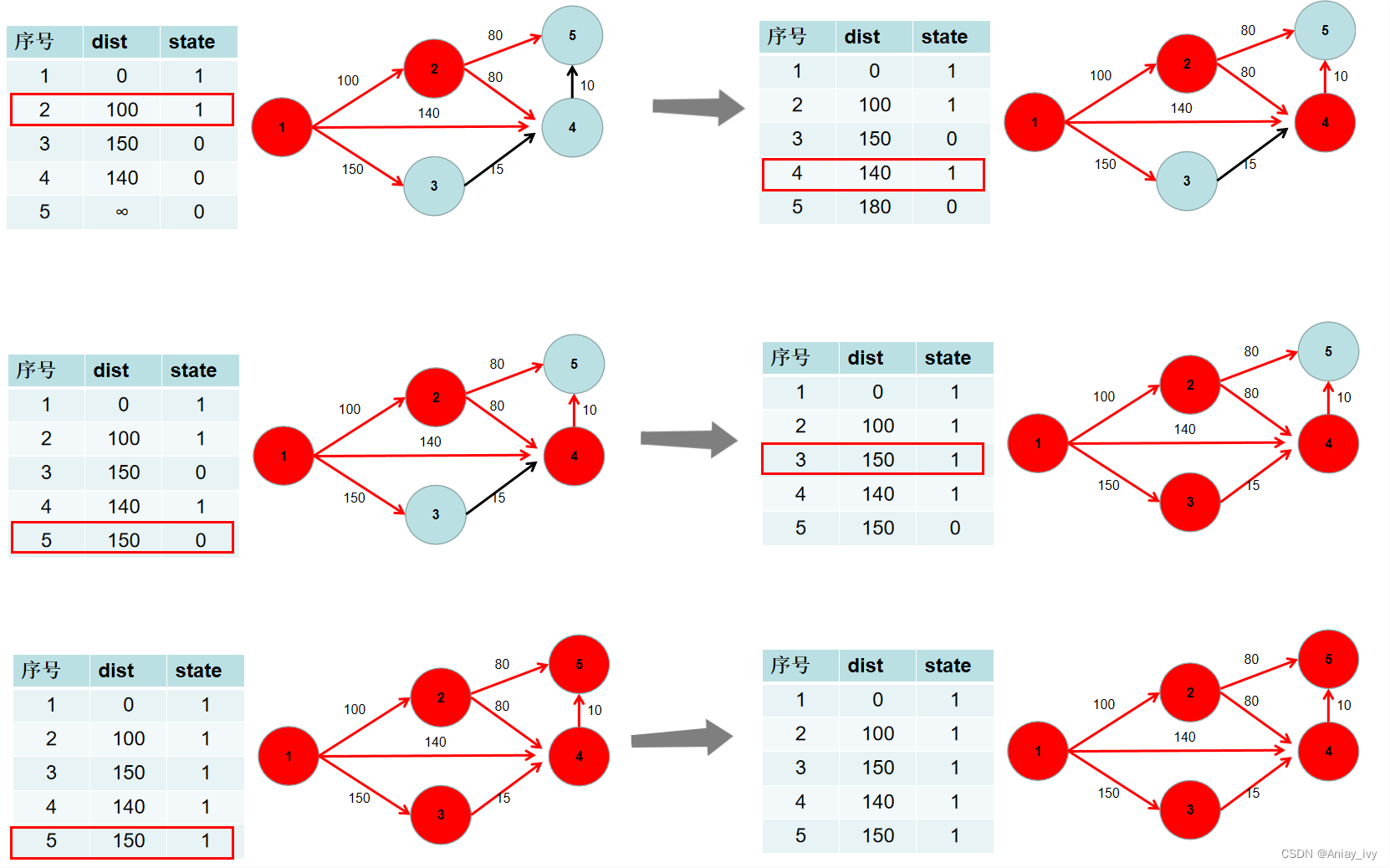
重复 3 4 步骤,直到所有节点的状态都被置为 1。
-
此时 dist 数组中,就保存了源点到其余各个节点的最短距离。

伪代码:
int dist[n],state[n];
dist[1] = 0, state[1] = 1;
for(i:1 ~ n)
{
t <- 没有确定最短路径的节点中距离源点最近的点;
state[t] = 1;
更新 dist;
}
代码
#include<iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010;
int h[N], e[M], ne[M], w[M], idx;//邻接表存储图
int state[N];//state 记录是否找到了源点到该节点的最短距离
int dist[N];//dist 数组保存源点到其余各个节点的距离
int n, m;//图的节点个数和边数
void add(int a, int b, int c)//插入边
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void Dijkstra()
{
memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大
dist[1] = 0;//源点到源点的距离为置为 0
for (int i = 0; i < n; i++)
{
int t = -1;
for (int j = 1; j <= n; j++)//遍历 dist 数组,找到没有确定最短路径的节点中距离源点最近的点t
{
if (!state[j] && (t == -1 || dist[j] < dist[t]))
t = j;
}
state[t] = 1;//state[i] 置为 1。
for (int j = h[t]; j != -1; j = ne[j])//遍历 t 所有可以到达的节点 i
{
int i = e[j];
dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]
}
}
}
int main()
{
memset(h, -1, sizeof(h));//邻接表初始化
cin >> n >> m;
while (m--)//读入 m 条边
{
int a, b, w;
cin >> a >> b >> w;
add(a, b, w);
}
Dijkstra();
if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了,则存在路径
cout << dist[n];
else
cout << "-1";
}
优化
看一下算法的时间复杂度:
for(i:1 ~ n)//n次
{
t <- 没有确定最短路径的节点中距离源点最近的点;//每次遍一遍历dist数组,n次的复杂度是O(n^2)
state[t] = 1;
更新 dist;//每次遍历一个节点的出边,n次遍历了所有节点的边,复杂度为O(e)
}
算法的主要耗时的步骤是从dist 数组中选出:没有确定最短路径的节点中距离源点最近的点 t。只是找个最小值而已,没有必要每次遍历一遍dist数组。
在一组数中每次能很快的找到最小值,很容易想到使用小根堆。可以使用库中的小根堆(推荐)或者自己编写。
优化代码:
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>//堆的头文件
using namespace std;
typedef pair<int, int> PII;//堆里存储距离和节点编号
const int N = 1e6 + 10;
int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接表存储图
int dist[N];//存储距离
bool st[N];//存储状态
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
heap.push({0, 1});//插入距离和节点编号
while (heap.size())
{
auto t = heap.top();//取距离源点最近的点
heap.pop();
int ver = t.second, distance = t.first;//ver:节点编号,distance:源点距离ver 的距离
if (st[ver]) continue;//如果距离已经确定,则跳过该点
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});//距离变小,则入堆
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
使用小根堆后,找到 t 的耗时从 O(n^2) 将为了 O(1)。每次更新 dist 后,需要向堆中插入更新的信息。所以更新dist的时间复杂度有 O(e) 变为了 O(elogn)。总时间复杂度有 O(n^2) 变为了 O(n + elongn)。适用于稀疏图。
Java代码
import java.util.*;
public class Main{
static int N = 510,n,m, max = 0x3f3f3f3f;
static int[][] g = new int[N][N];//存每个点之间的距离
static int[] dist = new int[N];//存每个点到起点之间的距离
static boolean[] st = new boolean[N];//存已经确定了最短距离的点
public static int dijkstra(){
Arrays.fill(dist,max);//将dist数组一开始赋值成较大的数
dist[1] = 0; //首先第一个点是零
//从0开始,遍历n次,一次可以确定一个最小值
for(int i = 0 ; i < n ; i ++ ){
int t = -1; //t这个变量,准备来说就是转折用的
for(int j = 1 ; j <= n ; j ++ ){
/***
* 因为数字是大于1的,所以从1开始遍历寻找每个数
* 如果s集合中没有这个数
* 并且t == -1,表示刚开始 或者 后面的数比我心找的数距离起点的距离短
* 然后将j 的值赋值给 t
***/
if(!st[j] && (t == -1 || dist[j] < dist[t])){
t = j;
}
}
st[t] = true;//表示这个数是已经找到了确定了最短距离的点
//用已经确认的最短距离的点来更新后面的点
//就是用1到t的距离加上t到j的距离来更新从1到j的长度
for(int j = 1 ; j <= n ; j ++ ){
//
dist[j] = Math.min(dist[j],dist[t] + g[t][j]);
}
}
//如果最后n的长度没有改变,输出-1,没有找到;否则输出最短路n
if(dist[n] == max) return -1;
else return dist[n];
}
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
m = scan.nextInt();
//将他们每个点一开始赋值成一个较大的值
for(int i = 1 ; i <= n ; i ++ ){
Arrays.fill(g[i],max);
}
while(m -- > 0){
int a = scan.nextInt();
int b = scan.nextInt();
int c = scan.nextInt();
g[a][b] = Math.min(g[a][b],c);//这个因为可能存在重边,所以泽出最短的
}
int res = dijkstra();
System.out.println(res);
}
}
总结
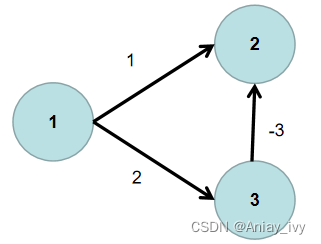
迪杰斯特拉算法适用于求正权有向图中,源点到其余各个节点的最短路径。注意:图中可以有环,但不能有负权边。
例如:如下图就不能使用迪杰斯特拉算法求节点 1 到其余各个节点的最短距离。