目录
前言
1.数组和结构体相关的一些知识
1.数组
2.结构体数组
3.递归遍历数组
2.二叉树的顺序存储表示法和实现
1.定义
2.初始化
3.先序遍历二叉树
4.中序遍历二叉树
5.后序遍历二叉树
6.完整代码
前言
二叉树的非递归的表示和实现。
1.数组和结构体相关的一些知识
1.数组
在C语言中,可以将数组作为参数传递给函数。当数组作为参数传递时,实际上传递给函数的是数组的地址,而不是数组的副本。这意味着,在函数内部对数组进行的修改会影响到原始数组。
例如在下面的代码中,我们把数组名作为参数传递给modifyArray函数,在函数中修改数组的值,main函数打印原来的数组,会发现原来的数组也被修改。
#include <stdio.h>
#include <stdlib.h>
void modifyArray(int *s,int size){
for (int i = 0; i < size; i++) {
s[i] = s[i] * 10;
}
printf("\n");
}
int main(int argc, const char *argv[]) {
int arr[5] = {1,2,3,4,5};
int length = sizeof(arr) / sizeof(arr[0]);
printf("修改之前的数组:\n");
for (int i = 0; i < length;i++) {
printf("%d\t",arr[i]);
}
modifyArray(arr,length);
printf("\n修改之前的数组:\n");
for (int i = 0; i < length;i++) {
printf("%d\t",arr[i]);
}
printf("\n");
return 0;
}
当然上述的函数我们还可以写成数组的形式。
void modifyArray(int s[],int size){
for (int i = 0; i < size; i++) {
s[i] = s[i] * 10;
}
printf("\n");
}2.结构体数组
在上述的代码中,我们使用数组操作基本数据类型非常的方便。当时当我们需要自定义数据类型的时候,上述的代码就不满足我们的需求了。例如我们需要表示学生数组的时候,因为每个学生都有自己的属性,姓名,年龄等等,这个时候我们就需要使用结构体数组。
在数据结构中,我们有时候需要使用数组表示一些数据类型,因此有时候我们需要把数组声明为全局函数。代码实例如下:
#include <stdio.h>
#include <stdlib.h>
// 学生结构体
typedef struct {
char name[50]; // 姓名
int age; // 年龄
} Student;
int main() {
// 创建一个包含3个学生对象的数组并初始化
Student students[3] = {
{"张三", 20},
{"李四", 21},
{"王五", 22}
};
// 输出学生信息
printf("学生信息如下:\n");
for (int i = 0; i < 3; i++) {
printf("学生姓名:%s\n", students[i].name);
printf("学生年龄:%d\n", students[i].age);
}
return 0;
}3.递归遍历数组
在我们使用数组表示二叉树的时候,需要递归遍历数组,这里需要您了解数组递归的写法。
在这个示例中以下面的代码为例,,recursivePrint 函数用于递归地遍历数组并打印数组中的元素。它接受三个参数:arr 表示数组,size 表示数组的大小,index表示当前遍历的索引位置。函数首先检查索引是否超出数组范围,如果是,则递归终止。否则,它打印当前索引处的数组元素,然后递归调用自身,传入下一个索引位置。在 main函数中,我们创建一个数组并调recursivePrint 函数来遍历打印数组元素。
#include <stdio.h>
// 递归遍历数组并打印数组中的元素
void recursivePrint(int arr[], int size, int index) {
// 递归终止条件:当索引超出数组范围时,结束递归
if (index >= size) {
return;
}
// 打印当前索引处的数组元素
printf("%d ", arr[index]);
// 递归调用,遍历下一个元素
recursivePrint(arr, size, index + 1);
}
int main() {
int arr[] = {1, 2, 3, 4, 5};
int size = sizeof(arr) / sizeof(arr[0]);
printf("数组元素为:");
recursivePrint(arr, size, 0);
printf("\n");
return 0;
}
2.二叉树的顺序存储表示法和实现
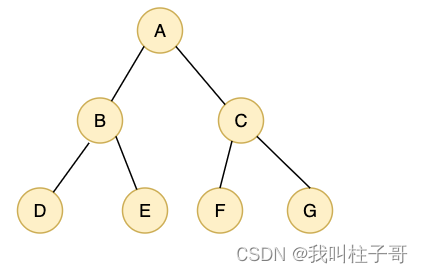
图1.完全二叉树
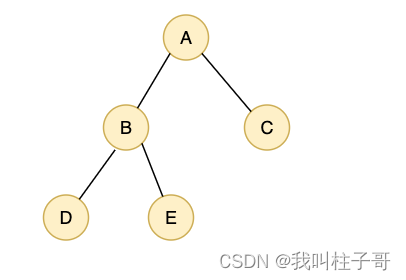
图2.普通二叉树
我们使用一组连续的存储空间表示树的结构。按照从上到下、从左到右的顺序存储完全二叉树的的节点,对于一般二叉树上的点,我们使用0表示不存在该节点。
对于图1来说,内存中的存储结构如下图3所示。

图3.完全二叉树的存储结构
如果不是二叉树,假如我们使用0表示结点不存在,图2所示的存储结构如图4所示。

图4.普通二叉树
下面我们看看如果使用代码来实现。
1.定义
我们使用数组实现二叉树的顺序存储
#define MAX_TREE_SIZE 100
typedef char TElemType;
typedef int Status;
typedef TElemType SqBiTree[MAX_TREE_SIZE];2.初始化
初始化时候,将数组中的元素全部设为"\0"
// 初始化二叉树
Status initSqBiTree(SqBiTree tree) {
for (int i = 0; i< MAX_TREE_SIZE; i++) {
tree[i] = '\0';
}
// 将二叉树所有元素初始化为空
return 1; // 初始化成功
}3.先序遍历二叉树
遍历二叉树之前我们观察下根节点、左子树节点、右子树节点的规律。
根节点的下标为a[0].左子树上的节点的下标依次为1,3,...2*i+1,右子树上的节点的下标依次为2,4,...2*i+2
// 前序遍历二叉树
void preOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 访问根节点
printf("%c ", tree[node_index]);
// 递归遍历左子树
preOrderTraverse(tree, 2 * node_index + 1);
// 递归遍历右子树
preOrderTraverse(tree, 2 * node_index + 2);
}
}4.中序遍历二叉树
// 中序遍历二叉树
void inOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 递归遍历左子树
inOrderTraverse(tree, 2 * node_index + 1);
// 访问根节点
printf("%c ", tree[node_index]);
// 递归遍历右子树
inOrderTraverse(tree, 2 * node_index + 2);
}
}5.后序遍历二叉树
// 后序遍历二叉树
void postOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 递归遍历左子树
postOrderTraverse(tree, 2 * node_index + 1);
// 递归遍历右子树
postOrderTraverse(tree, 2 * node_index + 2);
// 访问根节点
printf("%c ", tree[node_index]);
}
}6.完整代码
#include <stdio.h>
#define MAX_TREE_SIZE 100
typedef char TElemType;
typedef int Status;
typedef TElemType SqBiTree[MAX_TREE_SIZE];
// 初始化二叉树
Status initSqBiTree(SqBiTree tree) {
for (int i = 0; i< MAX_TREE_SIZE; i++) {
tree[i] = '\0';
}
// 将二叉树所有元素初始化为空
return 1; // 初始化成功
}
// 前序遍历二叉树
void preOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 访问根节点
printf("%c ", tree[node_index]);
// 递归遍历左子树
preOrderTraverse(tree, 2 * node_index + 1);
// 递归遍历右子树
preOrderTraverse(tree, 2 * node_index + 2);
}
}
// 中序遍历二叉树
void inOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 递归遍历左子树
inOrderTraverse(tree, 2 * node_index + 1);
// 访问根节点
printf("%c ", tree[node_index]);
// 递归遍历右子树
inOrderTraverse(tree, 2 * node_index + 2);
}
}
// 后序遍历二叉树
void postOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 递归遍历左子树
postOrderTraverse(tree, 2 * node_index + 1);
// 递归遍历右子树
postOrderTraverse(tree, 2 * node_index + 2);
// 访问根节点
printf("%c ", tree[node_index]);
}
}
int main(int argc, const char *argv[]) {
SqBiTree tree;
// 初始化二叉树
initSqBiTree(tree);
// 构造一个简单的二叉树,根节点为'A',左子树为'B',右子树为'C'
tree[0] = 'A';
tree[1] = 'B';
tree[2] = 'C';
tree[3] = 'D';
tree[4] = 'E';
tree[5] = '\0';
tree[6] = '\0';
// 输出初始化后的二叉树
printf("前序遍历结果为:");
preOrderTraverse(tree, 0);
printf("\n");
printf("中序遍历结果为:");
inOrderTraverse(tree, 0);
printf("\n");
printf("后序遍历结果为:");
postOrderTraverse(tree, 0);
printf("\n");
return 0;
}
// 后序遍历二叉树
void postOrderTraverse(SqBiTree tree, int node_index) {
if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {
// 递归遍历左子树
postOrderTraverse(tree, 2 * node_index + 1);
// 递归遍历右子树
postOrderTraverse(tree, 2 * node_index + 2);
// 访问根节点
printf("%c ", tree[node_index]);
}
}
int main(int argc, const char *argv[]) {
SqBiTree tree;
// 初始化二叉树
initSqBiTree(tree);
// 构造一个简单的二叉树,根节点为'A',左子树为'B',右子树为'C'
tree[0] = 'A';
tree[1] = 'B';
tree[2] = 'C';
tree[3] = 'D';
tree[4] = 'E';
tree[5] = '\0';
tree[6] = '\0';
// 输出初始化后的二叉树
printf("前序遍历结果为:");
preOrderTraverse(tree, 0);
printf("\n");
printf("中序遍历结果为:");
inOrderTraverse(tree, 0);
printf("\n");
printf("后序遍历结果为:");
postOrderTraverse(tree, 0);
printf("\n");
return 0;
}
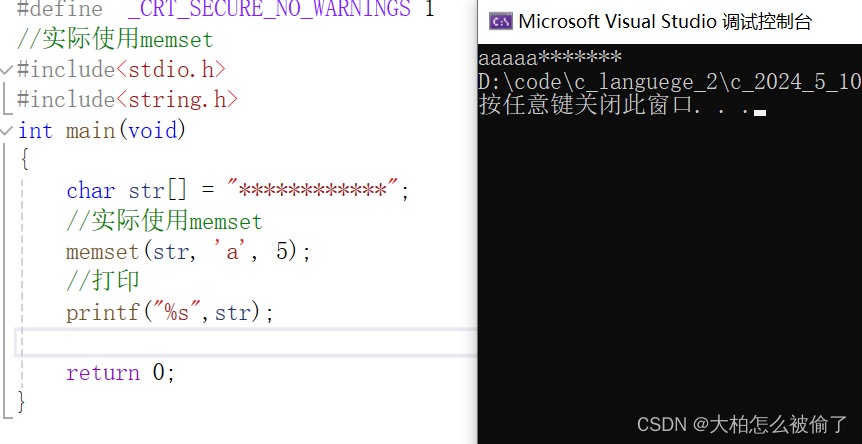
在main函数中,我们构建了一个图2所示的二叉树,控制台打印信息如下:









![[c++]多态的分析](https://img-blog.csdnimg.cn/direct/f1566f38456545a295c217543bcc7441.png)