1.KMeans算法是什么?
在没有标准标签的情况下,以空间的k个节点为中心进行聚类,对最靠近他们的对象进行归类。
2.KMeans公式:
2. 1.关键分为三个部分:
1.一开始会定义n个中心点,然后计算各数据点与中心点的距离:dist(xi,ujt)
2. 判断数据点属于哪一类:主要看当前数据点离哪一个中心点的距离最近
3.所有数据点分类完后,需要更新各个类的中心点,然后不断重复1,2操作直至中心点不再变化
中心点更新=1/k(当前区域的节点数)*(当前区域节点xi之和)

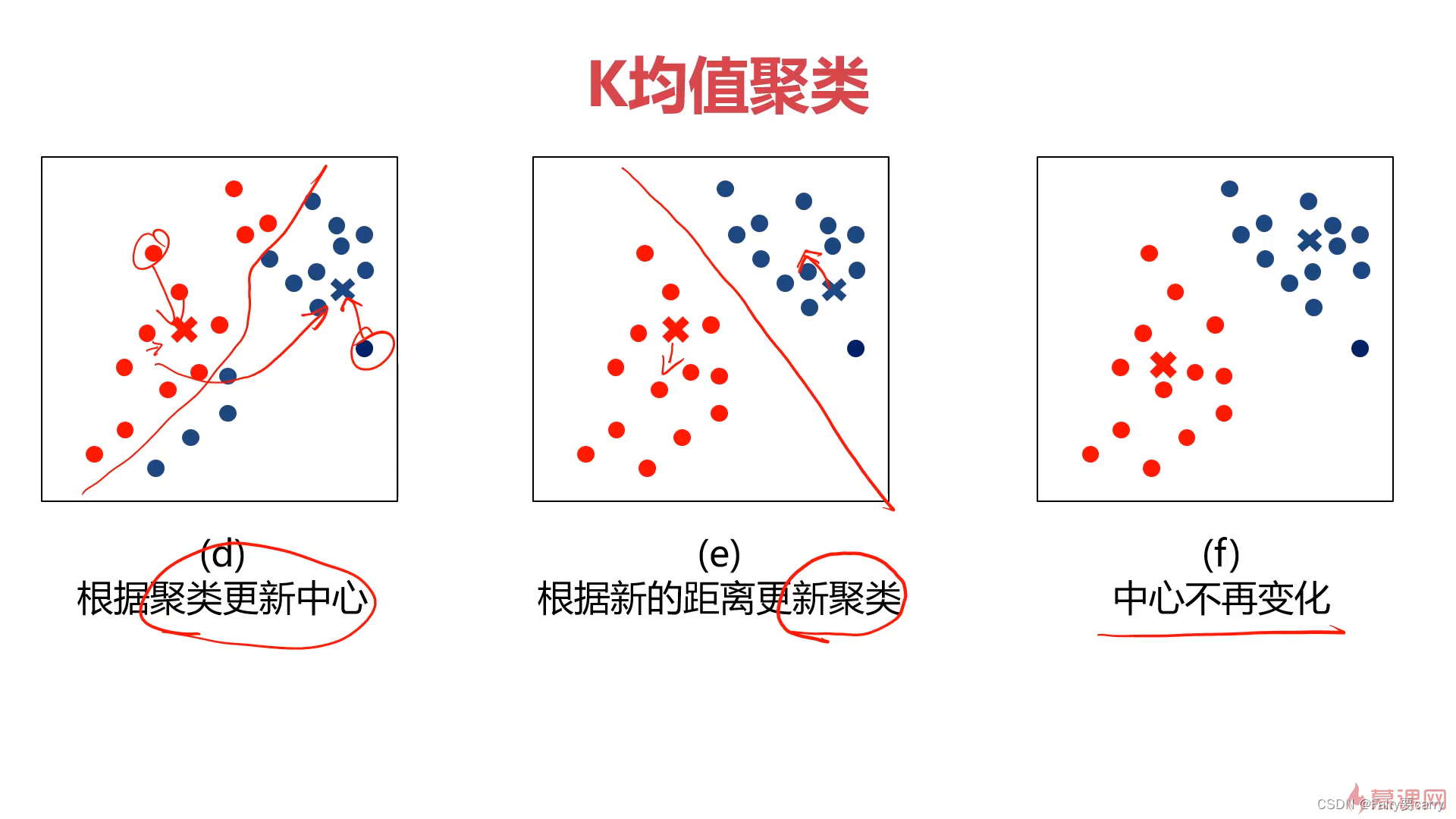
2.2.KMeans均值聚类的图像展示:
3.KNN算法
3.1.KNN算法是什么?
**1.概念:**给定一共训练数据集,对输入的新的数据实例A,在数据集上寻找和A实例最邻近的K各实例(K个邻居),然后这K个实例的多数属于某个类,那么这个A实例就属于该这个类中;
2.认识: 因为新实例的数据的判别,和它的K个邻居关系很大,所以我们需要知道K个邻居的正确标签,因此KNN算法是一个监督式学习的算法;

3.2.例子:

4.均值漂移聚类算法(Mean-shift)
4.1是什么?
KMeans算法需要一开始定义n个类别(n个中心点),但是如果数据量越来越大,类别越来越多时KMeans已经无法满足当前需求了。而均值漂移算法是一个基于密度梯度上升的聚类算法(沿着密度梯度上升,从而寻找聚类中心点)
因此Mean-shift是一个无监督学习算法。
4.2公式:
1.计算均值偏移:M(x)偏移量=1/K*(当前中心点和其余数据点的距离之和)
2.中心点的更新:新的中心点=旧的中心点+M(x)偏移量

4.3 均值漂移算法的流程:
**KMeans算法:*一开始定义n个中心类,然后根据与中心类的距离进行数据点的归类,并重复以上操作直至中心点不再变化(中心点=1/K(xi之和));
**Mean-shift算法:*随机找一个点作为中心点A,并定义半径r,找出与A距离在r内的所有节点记为集合S——>计算偏移量中心节点的均值偏移量(1/K(u-xi)),不断移动中心点A直至收敛

5.KMeans算法实战:
1.概念: 本质是一个非监督学习的聚类算法,也就是说不需要提供标签,它会以空间K个中心点进行聚类,对最靠近他们的对象进行归类。
2.过程: 1.首先KM = KMeans(n_clusters=3, random_state=0)选择中心点个数——>2.然后根据各个数据datai到中心点的距离确定各个datai所属的类别——>3.不断更新聚类中心(1/K*(xi之和))【k为每个区域的节点个数,xi为该区域的节点】直至中心点不再变化
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import accuracy_score
# 1.读取数据进行预览
data = pd.read_csv('D:/pythonDATA/data.csv')
data.head()
# 2.定义X和y
X = data.drop(['labels'], axis=1)
y = data.loc[:, 'labels']
y.head()
pd.value_counts(y) # 查看label类别数(0,1,2)
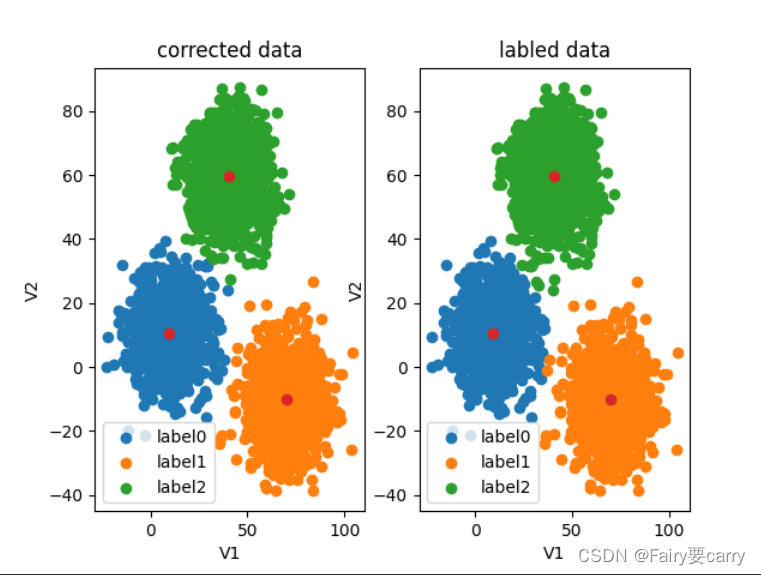
# 3.根据给定的正确的标签进行分类
fig1 = plt.figure()
label0 = plt.scatter(X.loc[:, 'V1'][y == 0], X.loc[:, 'V2'][y == 0])
label1 = plt.scatter(X.loc[:, 'V1'][y == 1], X.loc[:, 'V2'][y == 1])
label2 = plt.scatter(X.loc[:, 'V1'][y == 2], X.loc[:, 'V2'][y == 2])
plt.title('labeled data')
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0, label1, label2), ('label0', 'label1', 'label2'))
# 4.建立Kmeans模型:需要指定中心节点数3个
KM = KMeans(n_clusters=3, random_state=0)
KM.fit(X)
# 5.输出中心节点信息,并画出中心点
centers = KM.cluster_centers_
print("中心点信息:")
print(centers)
plt.scatter(centers[:, 0], centers[:, 1])
plt.show()
y_predict = KM.predict(X)
# 矫正结果
y_corrected = []
for i in y_predict:
if i == 0:
y_corrected.append(2)
elif i == 1:
y_corrected.append(1)
else:
y_corrected.append(0)
print(pd.value_counts(y_corrected), pd.value_counts(y))
# 预测模型
accuracy = accuracy_score(y, y_corrected)
print(accuracy)
6.KNN算法的实战
1.概念: 本质上是一个监督学习算法,数据需要提供正确的标签。
2.过程: 根据输入的数据实例寻找该实例最近的K个实例——>如果这K个实例的大多数属于A类,那么这个新输入的实例就属于A类
3.缺点: 1.需要指定K邻居数量,且需要给数据附上标签;2.没有中心节点
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import silhouette_score
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# 1. 读取数据进行预览
data = pd.read_csv('D:/pythonDATA/data.csv')
data.head()
# 2. 定义X和y
X = data.drop(['labels'], axis=1)
y = data.loc[:, 'labels']
# 3. 使用KNN算法进行聚类
k = 3 # 设定簇的数量
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X, y)
# 4. 预测每个样本所属的簇
y_predict = knn.predict(X)
y_predict = np.array(y_predict)
print(y_predict)
# 5. 评估聚类结果
silhouette_avg = silhouette_score(X, y_predict)
print("Silhouette Score:", silhouette_avg)
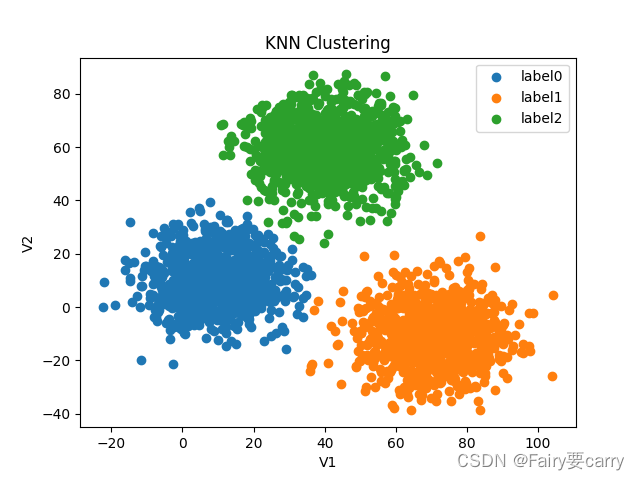
# 6. 画图(KNN不提供聚类中心,因此无法画出中心点)
label0 = plt.scatter(X.loc[:, 'V1'][y_predict == 0], X.loc[:, 'V2'][y_predict == 0])
label1 = plt.scatter(X.loc[:, 'V1'][y_predict == 1], X.loc[:, 'V2'][y_predict == 1])
label2 = plt.scatter(X.loc[:, 'V1'][y_predict == 2], X.loc[:, 'V2'][y_predict == 2])
plt.legend((label0, label1, label2), ('label0', 'label1', 'label2'))
plt.title("KNN Clustering")
plt.xlabel('V1')
plt.ylabel('V2')
plt.show()
y_predict_test = knn.predict([[80, 60]])
print(y_predict_test)
7.MeanShift算法的实战:
1.概念: 与KMeans算法一样是一个非监督学习算法,无需提供数据标签,也无需像KMeans算法一样提前定义中心节点的个数。
2.过程: 首先随机选一个没有分类的点作为中心点**(初始化)——>然后找出中心点A距离在r内的所有点,记为集合S (生成集合)——>再然后就是计算中心点A到集合S内每个元素的偏移量M(x) (确定方向)——>不断进行节点的更新并聚合直到所有的点都不再移动或者移动的距离小于一个设定的阈值(生成聚类)**
3.公式: 1.计算均值偏移:M(x)=1/K*(当前中心点和其余数据的距离差之和) ——>2.中心点的更新:新的中心点=旧的中心点+M(x) 偏移量
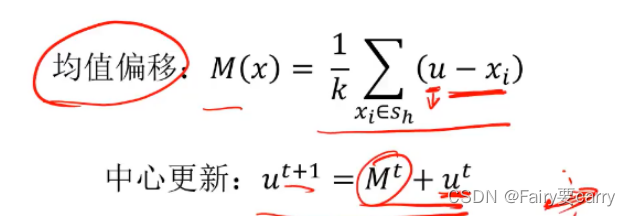
from sklearn.cluster import MeanShift, estimate_bandwidth
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.metrics import silhouette_score
# 1.读取数据进行预览
data = pd.read_csv('D:/pythonDATA/data.csv')
data.head()
# 2.定义X
X = data.drop(['labels'], axis=1)
y = data.loc[:, 'labels']
# 3.使用MeanShift算法进行聚类
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
meanshift = MeanShift(bandwidth=bandwidth)
meanshift.fit(X)
# 4.输出聚类中心信息
centers = meanshift.cluster_centers_
print("中心点信息:")
print(centers)
# 5.预测每个样本所属的簇
y_predict = meanshift.predict(X)
silhouette_avg = silhouette_score(X, y_predict)
print("Silhouette Score:", silhouette_avg)
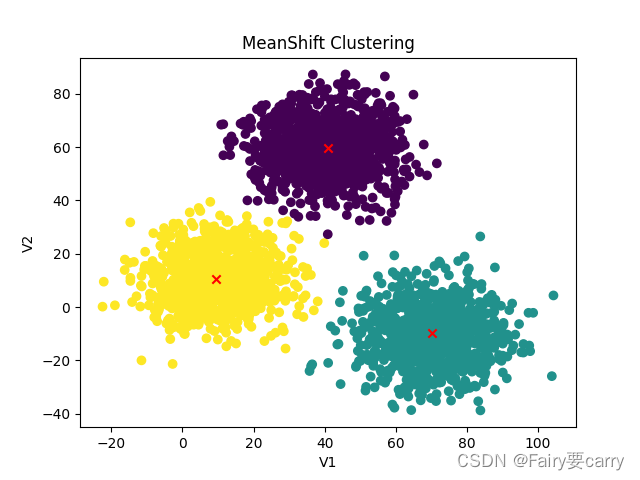
# 6.画图
plt.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y_predict)
plt.scatter(centers[:, 0], centers[:, 1], marker='x', color='red')
plt.title("MeanShift Clustering")
plt.xlabel('V1')
plt.ylabel('V2')
plt.show()
8.silhouette_score轮廓系数对于聚类的评分
-
是什么: **轮廓系数(Silhouette Score)**是一种用于评估聚类效果的指标,它考虑了聚类的紧密度和分离度。其计算方法如下:
-
对于每个
样本i,计算与同簇中所有其他样本的平均距离,记作ai。ai越小(优),表示样本i越应该被分到该簇。 -
对于
样本i,计算它与其他任意簇中所有样本的平均距离,取最小值,记作bi。bi越大(优),表示样本i越不应该被分到其他簇。 -
轮廓系数Si定义为:Si = (bi - ai) / max(ai, bi)
对所有样本的轮廓系数取平均值,得到整个数据集的平均轮廓系数。
轮廓系数的取值范围在[-1, 1]之间,其中:
- 如果Si接近于1,则表示样本i聚类合理,距离相近的样本分在同一个簇,且簇与其他簇有很好的分离度。
- 如果Si接近于-1,则表示样本i更适合分到其他簇,当前的聚类结果可能不合理。
- 如果Si接近于0,则表示样本i位于两个簇的边界附近。
所以,轮廓系数越大越好,表示聚类效果越好。









![[C++核心编程-06]----C++类和对象之对象模型和this指针](https://img-blog.csdnimg.cn/direct/3a1a6021b0d04cee9a1bdbe48682cca2.png)