C++算法题 - 图

news2024/11/20 4:45:37

目录

  • 200. 岛屿数量
  • 130. 被围绕的区域
  • 133. 克隆图
  • 399. 除法求值
  • 207. 课程表
  • 210. 课程表 II

200. 岛屿数量

LeetCode_link

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出：1

示例 2：
输入：grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出：3

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

思路：把图当作一个4叉树，然后出界条件的判断类似于二叉树中的if(root == nullptr) return;一样的判断，并且要注意不要重复访问，要将访问过的位置做标记

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int n = grid.size(), m = grid[0].size();
        int count = 0;
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(grid[i][j] == '1'){
                    count++;
                    paint(grid, i, j);
                }
            }
        }
        return count;
    }
    void paint(vector<vector<char>>& grid, int i, int j){
        int n = grid.size(), m = grid[0].size();
        if(i<0 || i>=n || j<0 || j>=m) return;
        if(grid[i][j] != '1')   return;
        grid[i][j] = '2';
        int a[4] = {1, 0, -1, 0};
        int b[4] = {0, 1, 0, -1};
        for(int k = 0; k < 4; k++){
            paint(grid, i+a[k], j+b[k]);
        }
    }
};

130. 被围绕的区域

LeetCode_link

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：
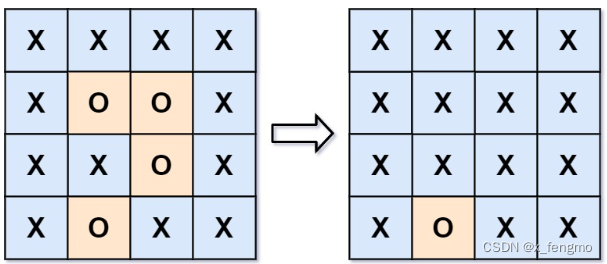
在这里插入图片描述
输入：board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
输出：[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：
输入：board = [[“X”]]
输出：[[“X”]]

提示：
m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

思路：分别把与边界相连的“根”和不与边界相连的“根”保存下来，之后再根据“根”进行染色

注意:
bool re = found(board, i+1, j) && found(board, i-1, j) && found(board, i, j+1) && found(board, i, j-1);
和
bool down = found(board, i+1, j);
bool up = found(board, i-1, j);
bool right = found(board, i, j+1);
bool left = found(board, i, j-1);
bool re = down && up && right && left;
是不一样的，如果是* && * && * && *的情况，如果第一个表达式的值是false，则后面的表达式都不会执行，因此，如果我们希望后面的函数依旧执行来进行染色，则不能合并成一个语句书写。

class Solution {
public:
    void solve(vector<vector<char>>& board) {
        int n = board.size(), m = board[0].size();
        stack<pair<int, int>> p;
        stack<pair<int, int>> nop;
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m ;j++){
                if(board[i][j] == 'O'){
                    if(found(board, i, j)){
                        p.push({i, j});
                    }else{
                        nop.push({i ,j});
                    }
                }
            }
        }
        while(!p.empty()){
            auto site = p.top();
            paint(board, site.first, site.second, 'X');
            p.pop();
        }
        while(!nop.empty()){
            auto site = nop.top();
            paint(board, site.first, site.second, 'O');
            nop.pop();
        }
    }
    bool found(vector<vector<char>>& board, int i, int j){
        if(i<0 || i>=board.size() || j<0 || j>=board[0].size()) return false;
        if(board[i][j] != 'O')  return true;
        board[i][j] = 'A';
        bool down = found(board, i+1, j);
        bool up = found(board, i-1, j);
        bool right = found(board, i, j+1);
        bool left = found(board, i, j-1);
        return down && up && right && left;
    }
    void paint(vector<vector<char>>& board, int i, int j, char c){
        if(i<0 || i>=board.size() || j<0 || j>=board[0].size()) return;
        if(board[i][j] != 'A')  return;
        board[i][j] = c;
        paint(board, i+1, j, c);
        paint(board, i-1, j, c);
        paint(board, i, j+1, c);
        paint(board, i, j-1, c);
    }
};

思路：先把边界的点作为“根”寻找一遍，标记上’A’。之后遍历全部，如果被标记为’A’的就是与边界相连的，如果不是’A’而是’O’的，则是不与边界相连的，直接置为’X’即可。

class Solution {
public:
    void solve(vector<vector<char>>& board) {
        int n = board.size(), m = board[0].size();
        for(int i = 0; i < n; i++){
            found(board, i, 0);
            found(board, i, m-1);
        }
        for(int i = 0; i < m; i++){
            found(board, 0, i);
            found(board, n-1, i);
        }
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(board[i][j] == 'A'){
                    board[i][j] = 'O';
                }else if(board[i][j] == 'O'){
                    board[i][j] = 'X';
                }
            }
        }
    }
    void found(vector<vector<char>>& board, int i, int j){
        if(i<0 || i>=board.size() || j<0 || j>=board[0].size()) return;
        if(board[i][j] != 'O')  return;
        board[i][j] = 'A';
        found(board, i+1, j);
        found(board, i-1, j);
        found(board, i, j+1);
        found(board, i, j-1);
    }
};

133. 克隆图

LeetCode_link

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：
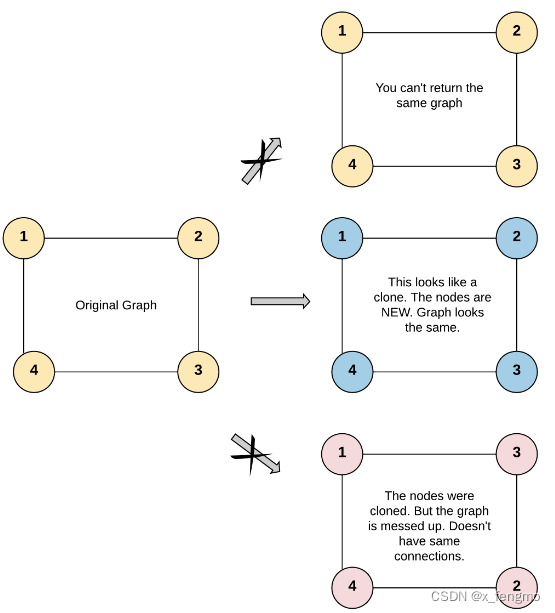
在这里插入图片描述
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：
在这里插入图片描述
输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：
输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

提示：
这张图中的节点数在 [0, 100] 之间。
1 <= Node.val <= 100
每个节点值 Node.val 都是唯一的，
图中没有重复的边，也没有自环。
图是连通图，你可以从给定节点访问到所有节点。

思路：hash中存储已经创建的新节点，并且可以用作判断是不是创建过，防止绕圈。用队列进行广度搜索。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
private:
    unordered_map<int, Node*> hash;
public:
    Node* cloneGraph(Node* node) {
        if(node == NULL)    return NULL;
        queue<Node*> q;
        Node* root = new Node(node->val);
        hash[node->val] = root;
        q.push(node);
        while(!q.empty()){
            Node* temp = q.front();
            Node* now_new = hash[temp->val];
            for(auto nei : temp->neighbors){
                if(hash.find(nei->val) == hash.end()){
                    q.push(nei);
                    Node* n = new Node(nei->val);
                    hash[nei->val] = n;
                }
                now_new->neighbors.push_back(hash[nei->val]);
            }
            q.pop();
        }
        return hash[node->val];
    }
};

399. 除法求值

LeetCode_link

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

注意：未在等式列表中出现的变量是未定义的，因此无法确定它们的答案。

示例 1：
输入：equations = [[“a”,“b”],[“b”,“c”]], values = [2.0,3.0], queries = [[“a”,“c”],[“b”,“a”],[“a”,“e”],[“a”,“a”],[“x”,“x”]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意：x 是未定义的 => -1.0

示例 2：
输入：equations = [[“a”,“b”],[“b”,“c”],[“bc”,“cd”]], values = [1.5,2.5,5.0], queries = [[“a”,“c”],[“c”,“b”],[“bc”,“cd”],[“cd”,“bc”]]
输出：[3.75000,0.40000,5.00000,0.20000]

示例 3：
输入：equations = [[“a”,“b”]], values = [0.5], queries = [[“a”,“b”],[“b”,“a”],[“a”,“c”],[“x”,“y”]]
输出：[0.50000,2.00000,-1.00000,-1.00000]

提示：
1 <= equations.length <= 20
equations[i].length == 2
1 <= Ai.length, Bi.length <= 5
values.length == equations.length
0.0 < values[i] <= 20.0
1 <= queries.length <= 20
queries[i].length == 2
1 <= Cj.length, Dj.length <= 5
Ai, Bi, Cj, Dj 由小写英文字母与数字组成

思路：先建图，有向图。之后深度搜索，以问题中的第一个串为根，找问题中的第二个串。
在这里插入图片描述

class Solution {
    struct Node{
        string s;
        vector<Node*> neiborhoods;
        vector<double> value;
        Node(string _s): s(_s),  neiborhoods(vector<Node*>()), value(vector<double>()) {}
    };
    unordered_map<string, Node*> hash;//用于建图时，为了不重复建节点
    unordered_set<string> flag;//用于找答案时，为了不兜圈子
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        //建图
        int n = equations.size(), m = equations[0].size();
        for(int i = 0; i < n; i++){
            if(hash.find(equations[i][0]) == hash.end()){
                Node* node = new Node(equations[i][0]);
                hash[equations[i][0]] = node;
            }
            if(hash.find(equations[i][1]) == hash.end()){
                Node* node = new Node(equations[i][1]);
                hash[equations[i][1]] = node;
            }
            //有向图，相反方向互为导数
            Node* left = hash[equations[i][0]];
            Node* right = hash[equations[i][1]];
            left->neiborhoods.push_back(right);
            left->value.push_back(values[i]);
            right->neiborhoods.push_back(left);
            right->value.push_back(1/values[i]);

        }
        //找答案
        vector<double> rec = {};
        for(int i = 0; i < queries.size(); i++){
            flag.clear();
            if(hash.find(queries[i][0]) == hash.end() || hash.find(queries[i][1]) == hash.end()){  
                rec.push_back(-1);
            }else{
                rec.push_back(find_road(queries[i][0], queries[i][1]));
            }
        }
        return rec;
    }
    double find_road(string a, string b){
        if(a == b)  return 1;
        flag.insert(a);
        int n = hash[a]->neiborhoods.size();
        for(int i = 0; i < n; i++){
            string neibor = hash[a]->neiborhoods[i]->s;
            if(flag.find(neibor) == flag.end()){
                double temp = find_road(hash[a]->neiborhoods[i]->s, b);
                if(temp > 0){
                    return temp * hash[a]->value[i];
                }
            }
        }
        return -1;
    }
};

207. 课程表

LeetCode_link

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：
1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同

思路：拓扑问题，需要记录入度信息。用列表存放入度为0的点，用于“学习”课程，可以直接学习，不需要前序课程了。需要统计每门课的后续节点。

class Solution {
    unordered_map<int, vector<int>> hash;
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        if(prerequisites.size() == 0)  return true;       
        queue<int> q;
        vector<int> indegrees(numCourses, 0);
        for(int i = 0; i < prerequisites.size(); i++){
            int first = prerequisites[i][0];
            int second = prerequisites[i][1];
            if(hash.find(second) == hash.end()){
                hash[second] = {first};
            }else{
                hash[second].push_back(first);
            }
            indegrees[first] ++;
        }
        for(int i = 0; i < numCourses; i++){
            if(indegrees[i] == 0){
                q.push(i);
            }
        }
        int now_node;
        while(!q.empty() && numCourses > 0){
            now_node = q.front();
            q.pop();
            numCourses--;
            if(hash.find(now_node) == hash.end())   continue;
            int next = hash[now_node].size();
            for(int i = 0; i < next; i++){
                indegrees[hash[now_node][i]]--;
                if(indegrees[hash[now_node][i]] == 0){
                    q.push(hash[now_node][i]);
                }
            }
        }
        if(numCourses > 0){
            return false;
        }
        return true;
    }
};

210. 课程表 II

LeetCode_link

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。

  • 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2：
输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

示例 3：
输入：numCourses = 1, prerequisites = []
输出：[0]

提示：
1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
所有[ai, bi] 互不相同

思路：与上一题相似

class Solution {
    unordered_map<int, vector<int>> hash;
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        queue<int> q;
        vector<int> rec;
        vector<int> indegrees(numCourses, 0);
        for(int i = 0; i < prerequisites.size(); i++){
            if(hash.find(prerequisites[i][1]) == hash.end()){
                hash[prerequisites[i][1]] = {prerequisites[i][0]};
            }else{
                hash[prerequisites[i][1]].push_back(prerequisites[i][0]);
            }
            indegrees[prerequisites[i][0]] ++;
        }
        for(int i = 0; i < numCourses; i++){
            if(indegrees[i] == 0){
                q.push(i);
            }
        }
        int now_course;
        while(!q.empty() && numCourses > 0){
            now_course = q.front();
            rec.push_back(now_course);
            numCourses --;
            q.pop();
            if(hash.find(now_course) == hash.end()) continue;
            for(int i = 0; i < hash[now_course].size(); i++){
                indegrees[hash[now_course][i]]--;
                if(indegrees[hash[now_course][i]] == 0){
                    q.push(hash[now_course][i]);
                }
            }
        }
        if(numCourses > 0)  return {};
        return rec;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1661755.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android 屏幕适配全攻略（中）-从九宫格到矢量图,揭秘Android多屏幕适配的正确打开方式

Android 屏幕适配全攻略（中）-从九宫格到矢量图,揭秘Android多屏幕适配的正确打开方式

在移动互联网时代&#xff0c;无论是小小的手机屏幕&#xff0c;还是大大的平板显示器&#xff0c;Android 应用都必须做到完美适配&#xff0c;给用户以极佳的体验。本文将剖析 Android 多屏幕适配背后的种种技术细节&#xff0c;为您揭开最佳实践的正确打开方式&#xff0c;让…
阅读更多...
ModuleSim 仿真找不到模块 module is not defined

ModuleSim 仿真找不到模块 module is not defined

提示如下&#xff1a; # vsim -t 1ps -L altera_ver -L lpm_ver -L sgate_ver -L altera_mf_ver -L altera_lnsim_ver -L cycloneive_ver -L rtl_work -L work -voptargs""acc"" pulse_generator_tb # Start time: 14:26:25 on May 10,2024 # ** Note: (…
阅读更多...
基于小波交叉谱分析的地震波走时变化测量（MATLAB）

基于小波交叉谱分析的地震波走时变化测量（MATLAB）

地震波在地球介质中传播&#xff0c;带来了丰富的地下介质物性的信息&#xff0c;为了解地球内部结构及运动变化提供了可能。地球内部地震波速度的差异是人们确定地球圈层结构和横向不均匀性的重要物理参数&#xff0c;地下介质应力的变化和积累是地震的孕育和发生的原因&#…
阅读更多...
Day7 字符串和常用数据结构

Day7 字符串和常用数据结构

文章目录 字符串和常用数据结构使用字符串使用列表生成式和生成器使用元组使用集合使用字典练习练习1&#xff1a;在屏幕上显示跑马灯文字。练习2&#xff1a;设计一个函数产生指定长度的验证码&#xff0c;验证码由大小写字母和数字构成。练习3&#xff1a;设计一个函数返回给…
阅读更多...
速卖通ip地址会相互影响吗？如何防止账号关联？

速卖通ip地址会相互影响吗？如何防止账号关联？

在跨境电商行业&#xff0c;大部分平台都是不允许一个卖家操作多个店铺的&#xff0c;如果被平台检测出账户关联&#xff0c;可能会被封店。在速卖通平台&#xff0c;会通过IP地址来判断是否经营多个账号吗?IP地址会使店铺相互影响吗? 一、速卖通IP地址会关联吗? 首先各位卖…
阅读更多...
内容安全（DPI和DFI解析）

内容安全（DPI和DFI解析）

内容安全前言&#xff1a; 防火墙的本质其实就是包过滤&#xff0c;我们通常所说的安全设备&#xff08;如&#xff1a;IPS、IDS、AV、WAF&#xff09;的检测重心是应用层。下一代防火墙基于传统防火墙的拓展能力&#xff0c;就是可以将以上的安全设备模块集成在一起&#xff0…
阅读更多...
LeetCode-1486. 数组异或操作【位运算 数学】

LeetCode-1486. 数组异或操作【位运算 数学】

LeetCode-1486. 数组异或操作【位运算 数学】 题目描述&#xff1a;解题思路一&#xff1a;暴力很简单。解题思路二&#xff1a;优化&#xff01;时间复杂度&#xff1a;O(1)。注释丰富&#xff0c;明了。解题思路三&#xff1a;精简版&#xff01; 题目描述&#xff1a; 给你…
阅读更多...
通俗的理解网关的概念的用途（三）：你的数据包是如何到达下一层的

通俗的理解网关的概念的用途（三）：你的数据包是如何到达下一层的

其实&#xff0c;这一章我写不好&#xff0c;因为这其中会涉及到一些计算和一些广播等概念&#xff0c;本人不善于此项。在此略述&#xff0c;可以参考。 每台设备的不同连接在获得有效的IP地址后&#xff0c;会根据IP地址的规则和掩码的规则&#xff0c;在操作系统和交换机&a…
阅读更多...
【吃透Java手写】3-SpringBoot-简易版-源码解析

【吃透Java手写】3-SpringBoot-简易版-源码解析

【吃透Java手写】SpringBoot-简易版-源码解析 1 SpringbootDemo2 准备工作2.1 Springboot-my2.1.1 依赖2.1.2 SpringBootApplication2.1.3 SJBSpringApplication2.1.3.1 run方法 2.2 Springboot-user2.2.1 依赖2.2.2 UserController2.2.3 UserApplication 2.3 分析run方法的逻辑…
阅读更多...
Codeforces Round 217 (Div. 2) A. Rook, Bishop and King（BFS）

Codeforces Round 217 (Div. 2) A. Rook, Bishop and King（BFS）

Rook, Bishop and King 题面翻译 【题目描述】 佩蒂亚正在学习国际象棋。他已经学会如何移动王、车和象。让我们提示你如何移动国象棋子。棋盘有 64 64 64个棋格&#xff0c;呈 8 8 8\times8 88正方形。一个格子可以用 ( r , c ) (r,c) (r,c)来表示—— r r r指行&#xff…
阅读更多...
乡村振兴的文化旅游融合：整合乡村文化资源与旅游资源，发展文化旅游产业，提升美丽乡村的文化内涵和旅游吸引力

乡村振兴的文化旅游融合：整合乡村文化资源与旅游资源，发展文化旅游产业，提升美丽乡村的文化内涵和旅游吸引力

一、引言 随着城市化进程的加速和人们精神文化需求的日益增长&#xff0c;乡村旅游逐渐成为旅游市场的新热点。乡村振兴战略的提出&#xff0c;为乡村旅游的发展提供了新的契机。在这一背景下&#xff0c;如何整合乡村文化资源与旅游资源&#xff0c;发展文化旅游产业&#xf…
阅读更多...
postman常用功能超全使用教程

postman常用功能超全使用教程

Postman 使用 一、Postman 简介 Postman是一个接口测试工具,在做接口测试的时候,Postman相当于一个客户端,它可以模拟用户发起的各类HTTP请求(如:get/post/delete/put…等等),将请求数据发送至服务端,获取对应的响应结果。 二、Postman 功能简介 三、Postman 下载安装 Post…
阅读更多...
crontab开启定时任务

crontab开启定时任务

linux上面可以使用crontab -e配置定时任务,但是一般需求进行一些配置才能使用,默认如下: crontab开启定时任务&#xff1a; 1.输入select-editor 2.选择 2. /usr/bin/vim.basic 有时候不需要第一步直接输入2就可以了,如下图所示 此时就可以在里面配置我们想要执行的定时任务…
阅读更多...
适合年轻人的恋爱交友脱单软件有哪些？中国十大社交软件排行榜分享

适合年轻人的恋爱交友脱单软件有哪些？中国十大社交软件排行榜分享

交友始祖&#xff1a;Tinder 一直很受欢迎&#xff0c;可以向上扫给 super like (每日有一次免费机会)。如果双方互相 like&#xff0c;代表配对成功&#xff0c;就可以开始聊天。另外&#xff0c;每日有 10 个 top picks 供选择&#xff0c;你可以免费选一位 主力编外&#xf…
阅读更多...
ETL免费工具kettle(PDI)，安装和配置

ETL免费工具kettle(PDI)，安装和配置

起源&#xff1a; Kettle最早是一个开源的ETL工具&#xff0c;全称为KDE Extraction, Transportation, Transformation and Loading Environment。在2006年&#xff0c;Pentaho公司收购了Kettle项目&#xff0c;原Kettle项目发起人Matt Casters加入了Pentaho团队&#xff0c;成…
阅读更多...
如何使用visual vm和jstat进行远程监控

如何使用visual vm和jstat进行远程监控

如何使用visual vm和jstat进行监控 安装visual vm 好像从jdk某个版本开始&#xff0c;jdk的bin目录下就不自带jvisualvm了&#xff0c;需要从官网下载一个visual vm。 打开visual vm Local是你本地的&#xff0c;无需多言。 先准备下必备的插件 如何通过visual vm观测远程…
阅读更多...
Windows程序设计课程作业-2（音乐文件播放功能）

Windows程序设计课程作业-2（音乐文件播放功能）

目录 1、作业内容 要求1&#xff1a; 提示&#xff1a; 要求2&#xff1a; 提示&#xff1a; 作业提交方式: 2、主要思路 1&#xff09;准备工作 2&#xff09;提取音乐文件功能 3&#xff09;选择音乐进行播放 4&#xff09;异常信息进行处理 5&#xff09;停止播…
阅读更多...
Apinto下载安装以及集群部署总结

Apinto下载安装以及集群部署总结

下载 下载官方提供的安装包安装&#xff08;推荐&#xff09; wget https://github.com/eolinker/apinto/releases/download/v0.13.3/apinto_v0.13.3_linux_amd64.tar.gz && tar -zxvf apinto_v0.13.3_linux_amd64.tar.gz && cd apinto 安装 先确保已经入解…
阅读更多...
Debian mariadb 10.11 XXXX message from server: “Too many connections“

Debian mariadb 10.11 XXXX message from server: “Too many connections“

问题表现 报错信息&#xff1a;Caused by: com.mysql.jdbc.exceptions.jdbc4.MySQLNonTransientConnectionException: Data source rejected establishment of connection, message from server: "Too many connections" 处理步骤 1、尝试能不能通过终端登录&…
阅读更多...
[报错解决]Communications link failure

[报错解决]Communications link failure

报错 主机IDEA项目连接虚拟机的数据库报错。 主要报错信息有&#xff1a; com.mysql.cj.jdbc.exceptions.CommunicationsException: Communications link failure The last packet sent successfully to the server was 0 milliseconds ago. The driver has not received a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023