Rook, Bishop and King

题面翻译

【题目描述】

佩蒂亚正在学习国际象棋。他已经学会如何移动王、车和象。让我们提示你如何移动国象棋子。棋盘有$64$个棋格，呈$8\times 8$正方形。一个格子可以用$(r,c)$来表示——$r$指行，$c$指列（虽然在经典棋局中用字母和数字一起表示）。每一个棋子占用一个棋格。一次合法的棋步就是执行如下之一：

• 车可以横向或纵向移动任意格。
• 象可以斜着移动任意格。
• 王可以任意方向移动一格——横着或者斜着。

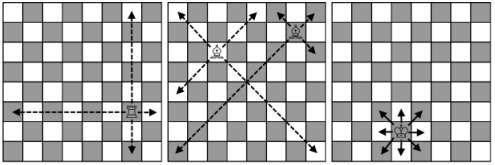
佩蒂亚在想，从$(r_1,c_1)$移动到$(r_2,c_2)$所需的最少步数是多少？我们假设在棋盘上只有一枚棋子。帮他解决问题。

【输入格式】

输入包括四个整数$r_1,c_1,r_2,c_2(1<=r_1,c_1,r_2,c_2<=8)$——分别代表出发的棋格和目的地棋格。数据保证两个格子不相同。你可以假设棋盘的行从上到下是$1$到$8$，棋盘从左到右是$1$到$8$。

【输出格式】

输出三个用空格分隔的整数，分别代表车、象、王从$(r_1,c_1)$移动到$(r_2,c_2)$所需的最少步数。如果无法移动到，则输出$0$。

题目描述

Little Petya is learning to play chess. He has already learned how to move a king, a rook and a bishop. Let us remind you the rules of moving chess pieces. A chessboard is 64 square fields organized into an $ 8×8 $ table. A field is represented by a pair of integers $ (r,c) $ — the number of the row and the number of the column (in a classical game the columns are traditionally indexed by letters). Each chess piece takes up exactly one field. To make a move is to move a chess piece, the pieces move by the following rules:

• A rook moves any number of fields horizontally or vertically.
• A bishop moves any number of fields diagonally.
• A king moves one field in any direction — horizontally, vertically or diagonally.

The pieces move like thatPetya is thinking about the following problem: what minimum number of moves is needed for each of these pieces to move from field $ (r_{1},c_{1}) $ to field $ (r_{2},c_{2}) $ ? At that, we assume that there are no more pieces besides this one on the board. Help him solve this problem.

输入格式

The input contains four integers $ r_{1},c_{1},r_{2},c_{2} $ ( $ 1<=r_{1},c_{1},r_{2},c_{2}<=8 $ ) — the coordinates of the starting and the final field. The starting field doesn’t coincide with the final one.

You can assume that the chessboard rows are numbered from top to bottom 1 through 8, and the columns are numbered from left to right 1 through 8.

输出格式

Print three space-separated integers: the minimum number of moves the rook, the bishop and the king (in this order) is needed to move from field $ (r_{1},c_{1}) $ to field $ (r_{2},c_{2}) $ . If a piece cannot make such a move, print a 0 instead of the corresponding number.

样例 #1

样例输入 #1

4 3 1 6

样例输出 #1

2 1 3

样例 #2

样例输入 #2

5 5 5 6

样例输出 #2

1 0 1

---

这道题和普通的BFS并无太大区别，在做的时候我会想到开一个结构体来记录坐标，步数和前一步操作，这个方法对于Rook和King都适用，但是对Bishop不行。

Bishop的移动过程是斜着移动多个距离，如果一个一个坐标的进行遍历，就会导致有些坐标会被封堵上，这样就导致有些情况是无法被扫出来的。

所以这道题BFS的正解其实是每次都遍历完路径上能够到达的所有点。

CODE：

#include<bits/stdc++.h>
using namespace std;
const int N = 15;
const int Rook_dx[4] = {1,-1,0,0};
const int Rook_dy[4] = {0,0,1,-1};
const int Bishop_dx[4] = {1,1,-1,-1};
const int Bishop_dy[4] = {1,-1,1,-1};
const int King_dx[8] = {1,0,-1,0,1,1,-1,-1};
const int King_dy[8] = {0,1,0,-1,1,-1,1,-1};
struct Node{
    int x,y;
    int step;
    int pre;
};
int r1,c1,r2,c2;
bool vis[N][N];

int bfs(int type){ //1:Rook,2"Bishop,3"King
    memset(vis,0,sizeof vis);
    int res = 2e9;
    queue<Node>q;
    q.push({r1,c1,0,10});

    vis[r1][c1] = 1;

    while(q.size()){
        Node t = q.front();
        q.pop();

        if(t.x == r2 && t.y == c2)return t.step;

        //cout << t.x << " " << t.y << " " << t.step << endl;

        if(type == 1){
            for(int i = 0;i < 4;i++){
                int x = t.x + Rook_dx[i],y = t.y + Rook_dy[i];
                if(x >= 1 && x <= 8 && y >= 1 && y <= 8 && !vis[x][y]){
                    vis[x][y] = 1;
                    if(t.pre == i) q.push({x,y,t.step,i});
                    else q.push({x,y,t.step + 1,i});
                }
            }
        }else if(type == 2){
            for(int i = 0;i < 4;i++){
                int x = t.x,y = t.y;
                while(x <= 8 && x >= 1 && y <= 8 && y >= 1){	//在没有超过边界的时候一直去走
                    if(!vis[x][y]){
                        q.push({x,y,t.step + 1,i});
                        vis[x][y] = 1;
                    }
                    x += Bishop_dx[i],y += Bishop_dy[i];
                }
            }
        }else{
            for(int i = 0;i < 8;i++){
                int x = t.x + King_dx[i],y = t.y + King_dy[i];
                if(x >= 1 && x <= 8 && y >= 1 && y <= 8 && !vis[x][y]){
                    vis[x][y] = 1;
                    q.push({x,y,t.step + 1,i});
                }
            }
        }
    }
    if(res == 2e9)return 0;
    else return res;
}

int main(){
    cin >> r1 >> c1 >> r2 >> c2;
    //bfs(2);
    cout << bfs(1) << " " << bfs(2) << " " << bfs(3) << " ";
    return 0;
}