参考文章思路：点我

题：C. Count Binary Strings

前言：嗯,今天做这个题的时候，想了一堆乱七八糟的解法，想记录一下$hh$。

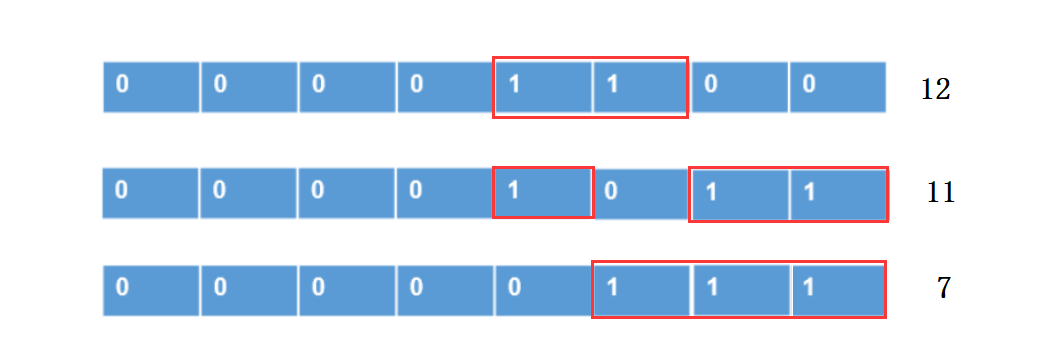
题意：输入以类似于邻接表的形式给出字符串（只由$0$和$1$组成）每一段之间的限制数，其中限制数这样规定：
当数值为$0$时：$[i,j]$段字符串没有限制
当数值为$1$时：$[i,j]$段字符串都是相同的
当数值为$2$时：$[i,j]$段字符串至少有$2$个字符是不一样的。

乱七八糟的思路：我最开始想的是把一个区间内限制数为1的给合并起来当作一个数来处理，反正都是相同的而且相邻。缩点的开始甚至想到了$tarjan$，但是实在不必，由于$n$比较小，直接暴力即可。接下来就是处理限制数为$2$的情况。（用合并之后的值作为新数进行计算。）我想的是求出来总的然后减去不符合条件的。
比如说$2\sim 4$之间又不符合条件的就把$2\sim 4$之间相同的给减掉，两边的话直接就$2$的$k$次幂组合。但是忽略了一个问题，这个有可能减的是重复的。当$5\sim 7$也有相同的的时候就重复了。后来又想的$dp$，这显然就区间$dp$，但是区间$dp$有一个弊端：当枚举区间$[i,j]$的时候，还要枚举$[i,j]$之间的点$k$，那么就有一个问题:$dp[i][j]$转移方程咋写？所以这个想法也是错的，在这种情况下：区间dp没法综合起子区间的情况。
由前所述，我想减去不满足条件的情况序列，然而一开始我想的不是枚举区间乘以两端，而是枚举左端点，看右端点最短能到哪，然后再减，减的时候其实是$\mathrm{111...};\mathrm{1111....};\mathrm{11111....};$后来才发现右边可以随便组合。
正解：还是说正经的$dp$吧。我们注意到如果把住一头，比如说就看第$i$位，那么由$i$向左看，看到某个$j$位，如果$[j,i]$的限制为$1$，而$[j-1,i]$的限制为$2$，那么$[1,i]$区间内的都应该为$2$.也就是$2222211111$的情况，最左的$1$是$j$位。现在枚举$[1,i]$区间内的$k$，如果$[k,i]$的区间为$1$，那么$k$应该在$j$的右边，并且可以重合；如果为$2$，那么$k$应该在$j$的左边，不能重合。
考虑状态转移：
设$dp[i][j]$为$[1,i]$区间以$j$为分界的方案数。那么

1. $dp[i+1][j]+=dp[i][j]$(在第$i+1$位上放一个和第$i$位相同的数）
2. $dp[i+1][i+1]+=dp[i][j]$(在第$i+1$位放一个和第$i$位不同的数）
   代码：

#include<iostream>
#include<cstdio>
const int length = 105;
int linjie[length][length];
int f[length][length];
typedef long long ll;
int mod = 998244353;
int main(void)
{
	int n;
	scanf_s("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		for (int j = i; j <= n; j++)
		{
			int a;
			scanf_s("%d", &a);
			linjie[i][j] = a;
			linjie[j][i] = a;
		}
	}
	f[1][1] = 2;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= i; j++)
		{
			int flag = 1;
			for (int k = 1; k <= i; k++)
			{
				if (linjie[k][i] == 1 && k < j)flag = 0;
				if (linjie[k][i] == 2 && k >= j)flag = 0;
			}
			if (!flag)
				f[i][j] = 0;
			f[i + 1][j] = ((ll)f[i+1][j]+f[i][j])%mod;
			f[i + 1][i + 1] =((ll)f[i+1][i+1]+ f[i][j])%mod;
		}
	}
	int sum = 0;
	for (int i = 1; i <= n; i++)
	{
		sum = ((ll)sum + f[n][i]) % mod;
	}
	printf("%d", sum);
}