目录
最近对问题
凸包问题
最近对问题
顾名思义就是采用蛮力法求出所有点之间的距离,然后进行比较找出第一个最近对,一个一个进行比较。
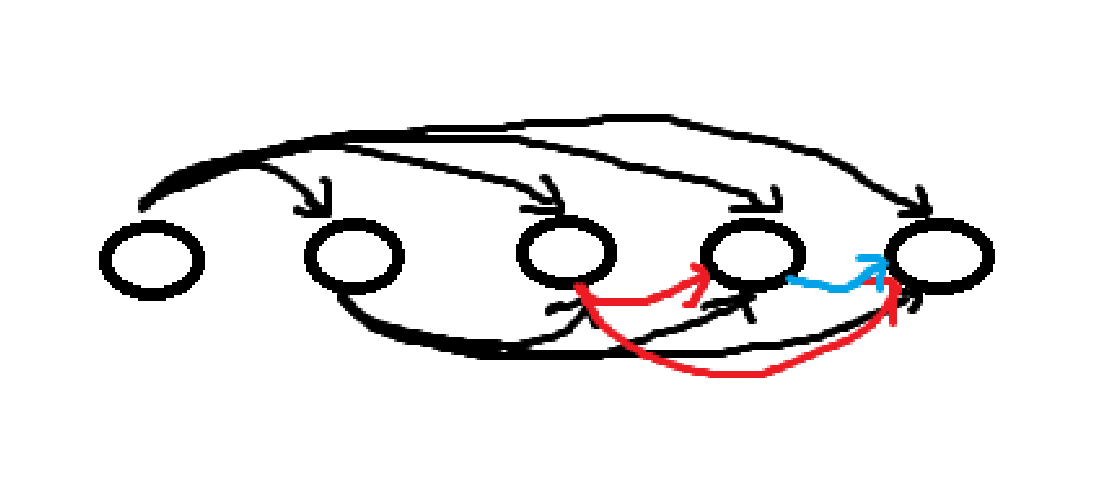
大概思路就是如图(每个圈代表一个数对)
第一个和其他四个比较
第二个和其他三个比较
.......
最后比较最小的
代码
图形化界面主要是easyx的graphics
#include<iostream>
#include <fstream>
#include<graphics.h>
#include <conio.h>
using namespace std;
#define Max 20 //20个点的凸包问题
#define maxn 10000
#define time 15
typedef struct {
int a;
int b;
}point;
void draw_point(point x[]);
void draw_line(int a, int b, int c, int d);
void judge(point x[]);
int main() {
point x[Max];
ifstream in("a.txt");
cout << "从txt中读取点坐标如下:" << endl;
for (int i = 0; i < 20; i++)
{
in >> x[i].a;
in >> x[i].b;
}
for (int i = 0; i < 20; i++)
{
cout << i + 1 << ":" << "(" << x[i].a << "," << x[i].b << ")" << endl;
}
cout << endl << endl;
in.close();
cout << "存储的数据如下:" << endl;
draw_point(x);
judge(x);
getchar();
return 0;
}
void judge(point x[]) {
int i, j, a, b, c, n, num1 = 0, num2 = 0;
int flag;
for (i = 0; i < Max; i++)
{
for (j = i + 1; j < Max; j++)
{
b = x[i].a - x[j].a;
a = x[j].b - x[i].b;
c = x[i].a * x[j].b - x[j].a * x[i].b;
for (n = 0; n < Max; n++)
{
if (n != i && n != j)
{
flag = x[n].a * a + x[n].b * b;
if (flag < c)
num1++;
else if (flag > c)
num2++;
else {
num1++;
num2++;
}
;
}
}
if (num1 == 18 || num2 == 18)
{
cout << "如下两点是极边:" << "(" << x[i].a << "," << x[i].b << ")" << "(" << x[j].a << "," << x[j].b << ")" << endl;
draw_line(x[i].a, x[i].b, x[j].a, x[j].b);
}
num1 = num2 = 0;
}
}
}
void draw_point(point x[]) {
initgraph(880, 680, SHOWCONSOLE);
setorigin(320, 240);
int a, b;
for (int i = 0; i < Max; i++) {
a = x[i].a * time;
b = x[i].b * time;
fillcircle(a, b, 4);
}
}
void draw_line(int a, int b, int c, int d)
{
line(a * time, b * time, c * time, d * time);
}运行结果
先写一个a.txt文件的点(20个)

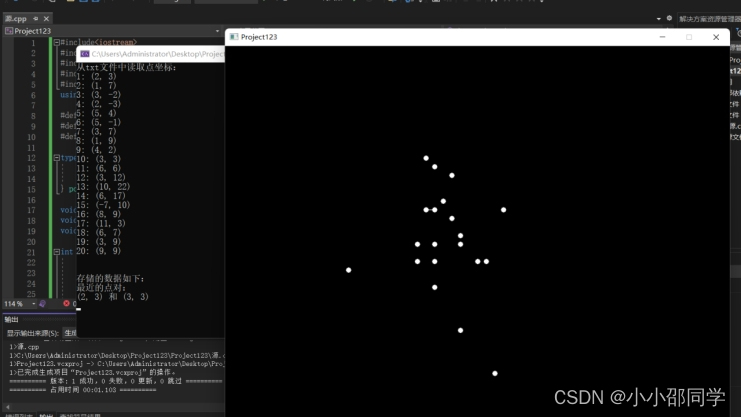
运行(可视化界面)

凸包问题
凸包问题就是在一个有n个点集的平面上,找出所有的“极点”,这些极点所构成的边界能够把其他所有的点都能包含在内。
思路
由两个点连起来的直线会将平面分成两部分,其中半个平面的点都满足ax+by>c ,另一半平面中的点都满足ax+by<c ,对于线上的点来说满足ax+by=c。因此,算法的思路就是对于每个点带入ax+by-c,判断表达式结果的符号是否相同即可。
代码
#include<iostream>
#include<fstream>
#include<graphics.h>
#include<cmath>
#include<algorithm>
using namespace std;
#define Max 20 // 最大点数
#define maxn 10000
#define time 15
typedef struct {
int a;
int b;
} point;
void draw_point(point x[]);
void draw_line(int a, int b, int c, int d);
void closest_pair(point x[]);
int main() {
point x[Max];
ifstream in("points.txt");
cout << "从txt文件中读取点坐标:" << endl;
for (int i = 0; i < Max; i++) {
in >> x[i].a;
in >> x[i].b;
}
for (int i = 0; i < Max; i++) {
cout << i + 1 << ": (" << x[i].a << ", " << x[i].b << ")" << endl;
}
cout << endl << endl;
in.close();
cout << "存储的数据如下:" << endl;
draw_point(x);
closest_pair(x);
getchar();
closegraph(); // 关闭图形窗口
return 0;
}
void closest_pair(point x[]) {
int min_distance = INT_MAX;
int pair1 = -1, pair2 = -1;
for (int i = 0; i < Max; i++) {
for (int j = i + 1; j < Max; j++) {
int distance = pow(x[i].a - x[j].a, 2) + pow(x[i].b - x[j].b, 2);
if (distance < min_distance) {
min_distance = distance;
pair1 = i;
pair2 = j;
}
}
}
cout << "最近的点对:" << endl;
cout << "(" << x[pair1].a << ", " << x[pair1].b << ") 和 (" << x[pair2].a << ", " << x[pair2].b << ")" << endl;
// 绘制最近的点对连线
draw_line(x[pair1].a, x[pair1].b, x[pair2].a, x[pair2].b);
}
void draw_point(point x[]) {
initgraph(880, 680, SHOWCONSOLE);
setorigin(320, 240);
int a, b;
for (int i = 0; i < Max; i++) {
a = x[i].a * time;
b = x[i].b * time;
fillcircle(a, b, 4);
}
}
void draw_line(int a, int b, int c, int d) {
line(a * time, b * time, c * time, d * time);
}运行结果
先写一个points.txt文件的点(20个)

运行:(可视化界面)