好题总结汇总

总结一些做完很有收获的题。

---

一、经典问题 + DP的结合

1、题意：

给定 $n$ 种颜色的球的数量 $a_1,a_2,...,a_n$，选出一些不同种类的球(也就是在n种球中选球的任意情况)，将球两两组合并且这两个球不能一致，或者将1个球看成一组，找到选出来的这些球的最小组数，球所有情况的最小组合数之和。

2、总结:

(1) 先对 $a$ 数组进行排序。

(2) 假如我们已经选到了 $n$ 个球的数量 $a_1,a_2,...,a_n,a_1\le a_2\le ...\le a_n$ 按照k个不同小球组合在一起或者是1个个组合的最小组合数是多少?
结论是：
$result=max(a[n],ceil(\sum a[i]/k))$

(3) 当我们有个这个结论，我们就可以直接进行背包 $dp$ 了，定义 $dp$ 数组为：$dp[i][j]$，表示前i个物品中必选 $a[i]$, $a[i]$ 为最大值，且体积为 $j$ 的方案数。
转移方程为：$dp[0][0]=1,dp[i][j]=\sum dp[1....i-1][j]$，复杂度 $O(n^2)$。

(4) 求取答案，$Ans=\sum dp[i][j]\ast max(a[i],ceil(j/k))$

3、代码：

#include <bits/stdc++.h> 
#define int long long 
using namespace std; 
const int N = 5010 + 10; 
const int mod = 998244353; 
int n, m; 
int a[N];
int dp[N][N]; 
void solve() {
    cin >> n; 
    for(int i = 1; i <= n; ++ i ) cin >> a[i]; 
    sort(a + 1, a + 1 + n); 
    
    dp[0][0] = 1; 
    
    int su[N] {0};
    su[0]=1;
    dp[0][0]=1;
    for(int i = 1; i <= n; ++ i ) {
        for(int j = a[i]; j <= 5000; ++ j ) { 
            dp[i][j] += su[j-a[i]];
            // su[j] = (dp[i][j] + su[j]) % mod; 
        }
        for(int j = 0; j <= 5000; ++ j ) 
            su[j] = (su[j] + dp[i][j]) % mod;
    }
    // cout<<dp[1][1]<<endl;
    int ans = 0; 
    for(int i = 1; i <= n; ++ i ) 
        for(int j = 0; j <= 5000; ++ j ) {
            ans = (ans + dp[i][j] * max((int)ceil(j * 1.0 / 2), a[i]) % mod) % mod;
            // cout<<dp[i][j]<<' '<<max((int)ceil(j * 1.0 / 2), a[i])<<endl;
        }
    cout<<ans<<endl;
}
signed main() {
    int ts = 1;  
    // cin >> ts; 
    while(ts -- ) solve(); 
    
    return 0; 
}

---

二、数学公式推导

1、题意：

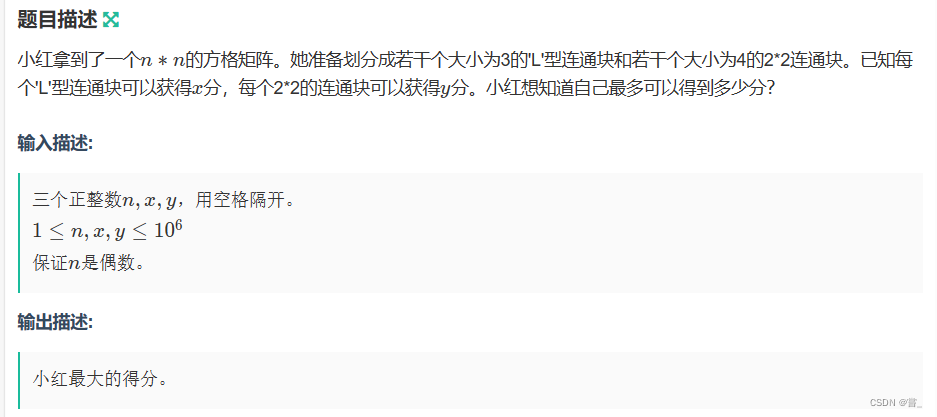
2、题解：

非常妙的一道题，直接开始推导：
假设我们划分 $a$ 个’L’形，$b$ 个2*2连通块。
我们可以得到一个方程组：
设 $T$ 是一个未知的非负整数，满足 $a\ast 3+b\ast 4=T$
$b=(T-3\ast a)/4$
$f(a,b)=f(a,(T-3\ast a)/4)=a\ast x+b\ast y=a\ast x+(T-3\ast a)/4\ast y=(x-3\ast y/4)\ast a+T\ast y/4$
我们发现就是一个有关a的一次函数，我们分类讨论根据单调性求即可。

3、代码:

#include<bits/stdc++.h>
#define int long long 
using namespace std; 
const int N = 1e5 + 10; 

int n,x,y;
signed main() {
    cin>>n>>x>>y;
    if(n==2){
        cout<<max(x,y)<<endl;
        return 0; 
    }
    if(x * 4 == 3 * y) {
        cout<<y*n*n/4<<endl;
        return 0; 
    } 
    
    if(x * 4 <= 3 * y) {
        cout<<n*n/4*y<<endl;
    }
    else {
        int ans=n*n/3*x;
        if(n*n%3) {
            ans-=(x-max(x,y));
        }
        cout<<ans<<endl;
    }
    
    return 0; 
}

---

三、