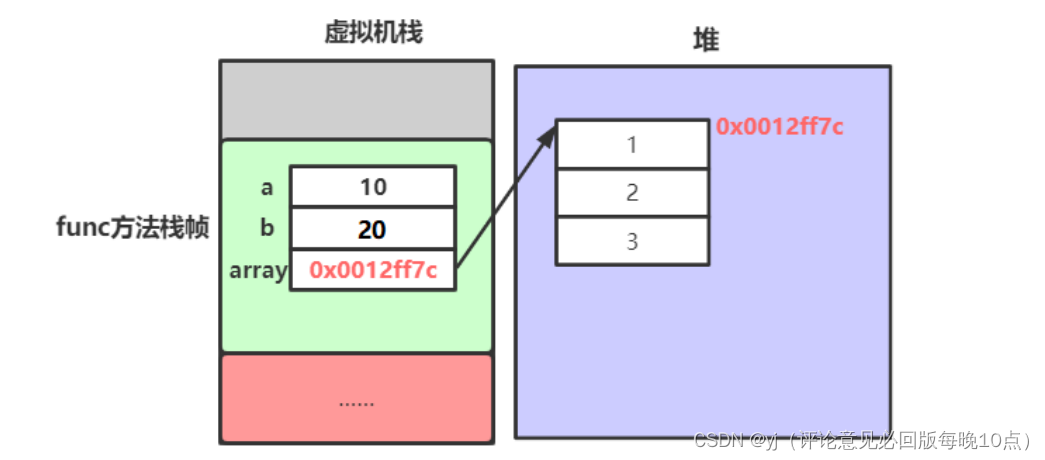
42.接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
- 我的原始人解法:遍历每个高度,然后从当前高度往后找,如果存在大于等于它的高度,就计算一次收集的雨水。比如 [4,1,2,5],那么收集的雨水量就是
(4-4) + (4-1) + (4-2),如果没有比它大的,由于雨水量只取决于低的高度,所以我们可以将其更新成他后面的第二高的高度,下一轮继续处理这一处,看能够和后面大于等于它的高度接多少雨水。 -
public int trap(int[] height) { int n = height.length; int res = 0; for(int i = 0; i < n - 1; i++){ int j = i + 1; int max = Integer.MIN_VALUE; while(j < n && height[j] < height[i]){ max = Math.max(max, height[j]); j++; } // 后面存在大于等于它的高度 if(j < n){ res += sum(height, i, j); i = j - 1; }else{ height[i] = max; i -= 1; } } return res; } // 计算 start ~ end 的雨水 public int sum(int[] height, int start, int end){ int sum = 0; for(int i = start; i < end; i++){ sum += height[start] - height[i]; } return sum; } - 前后缀分解:其实某一处的高度能否和前后组成接雨水的桶,取决于前后最大高度中的小的那个,所以求出对于每一个 height[i] 它的前面最大值 preMax[i] (0~i) 以及后面最大值 sufMax[i] (i~n-1) 就能知道这一处所能接的雨水量。比如 [1,2,0,3,5],对于 height[2] 的 0 来说,preMax[2] = 2, sufMax[2] = 5,那么它能储存的雨水就是
min(preMax[2],sufMax[2]) - height[2] -
public int trap(int[] height) { int n = height.length; int[] preMax = new int[n]; preMax[0] = height[0]; for(int i = 1; i < n; i++){ preMax[i] = Math.max(preMax[i-1], height[i]); } int[] sufMax = new int[n]; sufMax[n-1] = height[n-1]; for(int i = n-2; i >= 0; i--){ sufMax[i] = Math.max(sufMax[i+1], height[i]); } int res = 0; for(int i = 0; i < n; i++){ res += Math.min(preMax[i], sufMax[i]) - height[i]; } return res; } - 相向双指针: 根据上个解法可以优化,由于我们对于 preMax 以及 sufMax 数组的每个值都只需要在遍历到对应下标时用到一次,所以我们可以尝试用双指针和两个变量代替数组。遍历时不断更新 left 对应的 preMax 以及 right 对应的 sufMax,哪个 max 更小我们就将哪一边可以接的雨水计算一遍,对于这一边来说,和使用数组是等效的,而另一边如果实际上的 max 更大,那我们依旧是取这一边,所以没有影响。比如 [1,0,20,1],当我们遍历到高度为 0 处时,我们的 preMax=1, sufMax = 1,然后实际上 preMax=1, sufMax = 20,但这并不影响我们最终的计算结果,因为可接雨水只和更小的最大值有关,所以我们都取了小于等于 sufMax 的 preMax。即我们计算高度的那一边的 max 是实际上的 max,而另一边的 max 只可能大于等于这一边的 max,大于或等于都对结果无法造成影响。
-
public int trap(int[] height) { int res = 0; int left = 0, right = height.length - 1; int preMax = 0, sufMax = 0; while(left < right){ preMax = Math.max(preMax, height[left]); sufMax = Math.max(sufMax, height[right]); res += preMax <= sufMax? preMax - height[left++] : sufMax - height[right--]; } return res; } - 单调栈:以上的解法为计算每一列的雨水相加,而单调栈则为计算每一行的雨水。令单调栈存储高度降低的趋势,比如 [2,1],当遇到上升趋势时(高度大于栈顶元素对应高度,此例为 1)就能计算该区间某一行的雨水,比如遇到了 3,那么 [2,1,3] 就组成一个高度降低又上升的图形,即形成了一个桶。
- 雨水的面积我们采用长乘宽的形式计算,高我们需要取短边,即 2 和 3 中的 2,但还需要减去底边的高度,即高为 min(2,3) - 1,而宽则为 2,3 间相差的距离,为了计算宽度我们的栈就不能存储高度了,需要改为存储对应下标。这样比如 height = [2,1,3],我们的栈会存储 [0,1],遍历到 2 时高还是一样为
min(height[0],height[2]) - height[1],而宽直接就是2 - 0 - 1 - 单调栈算法的执行过程可以参考官方题解示意图
-
public int trap(int[] height) { int res = 0; Stack<Integer> stack = new Stack<>(); for(int right = 0; right < height.length; right++){ // 遇到上升趋势表示可能有桶了,因为如果前面没有下降趋势就还是没有桶,所以说可能 while(!stack.isEmpty() && height[right] > height[stack.peek()]){ // 底边 int bottom = stack.pop(); // 如果前面没有高度了就没法组成桶了 if(stack.isEmpty())break; // 左高度 int left = stack.peek(); // 宽为右高度下标 - 左高度下标 - 1 int currentWidth = right - left - 1; // 高为小高度减底边高度 int currentHeight = Math.min(height[left], height[right]) - height[bottom]; res += currentWidth * currentHeight; } stack.push(right); } return res; }