方法
Java中的方法就是c语言中的函数。
方法的定义
定义格式如下
修饰符 返回值 方法名([参数列表]){
代码块
[return 返回值;]
}
//方括号[]括起来代表可以没有,不是必须有的
方法名采用小驼峰命名(就是有多个单词,第一个单词首字母小写其余单词首字母大写),
方法不能嵌套定义(就是不能在方法中在定义一个方法),
例如我们定义一个加法函数
public static int add(int a, int b){
return a + b;
}
方法的传参
方法的传参就是根据定义的方法传入对应的参数就行
例如调用上面的加法方法
int c = add(1,3);
在方法中对参数进行改变时,要注意如果参数是基本数据类型,那一般对行参改变并不会影响实参。
例如下面这个函数当传过来实参后实参并不会改变。
public static void change(int a){
a = 5;
}
方法的重载(一词多义)
在我们现实调用函数实现加法时,有可能是3个参数相加,那我们又要重新定义一个3个参数的方法并且还不能与上一个加法方法重名。那未免太过繁琐,调用也过于麻烦。
这时在Java中我们可以实行对方法的重载来解决这种情况。
先说重载规则:
函数名必须相同,
参数列表必须不同(参数的个数不同、参数的类型不同、类型的次序必须不同),
与返回值无关
那下面来实现加法方法的重载
public static int add(int a, int b){
return a + b;
}
public static int add(int a, int b,int c){
return a + b + c;
}
在调用加法方法时,会自己根据你传的参数来判断调用哪一个。
函数递归调用
函数递归调用就是在函数自己内部在调用自己。但是一定要写好结束条件不然就会一直调用下去,导致栈溢出。
我们举个简单的递归求阶乘
public static int fac(int n){
if( n == 1){
return 1;
}
return n * fac(n - 1);
}
数组
数组的定义
类型[] 数组名 = {};//在大括号中输入所有数据初始化
类型[] 数组名 = new 类型[]{};//在大括号中输入所有数据初始化
类型[] 数组名 = new 类型[];//在中括号中输入数组大小,这种定义会直接给赋值为类型对应‘0’值
类型对应‘0’值如下
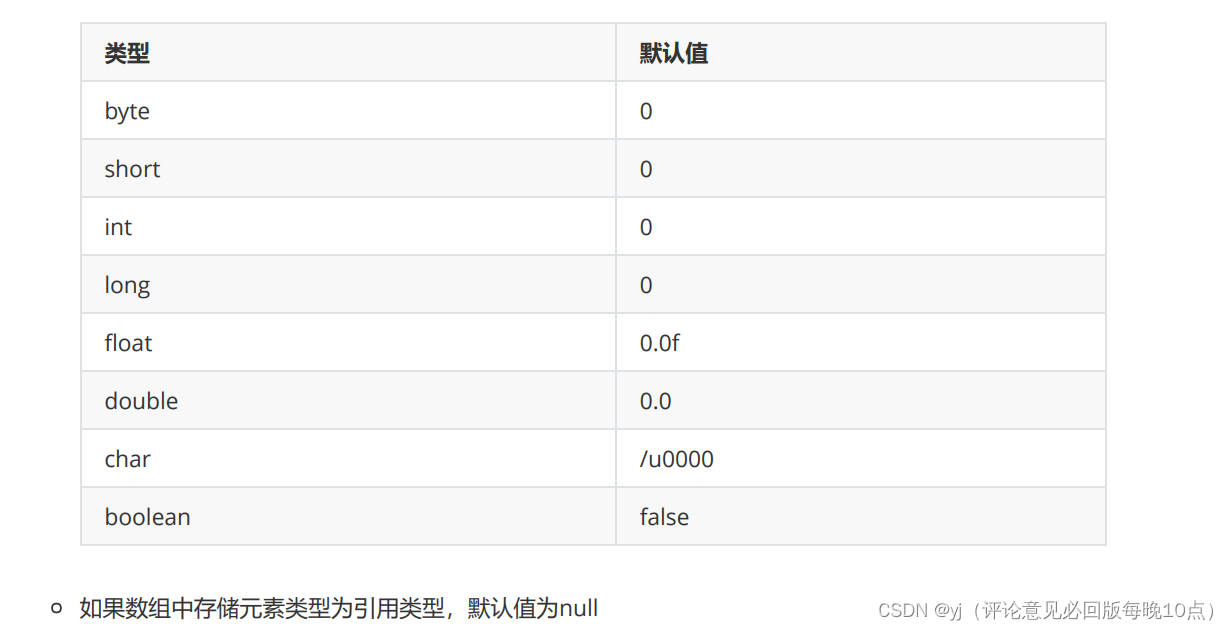
数组的使用
在c语言中我们要想获得数组长度需要进行计算,但在Java中只需要用数组名.length来就可以求得。
数组的for循环遍历方式有两种
int[] array = new int[10];
for(int i = 0; i < array.length; i++){
System.out.print("%d ", array[i]);
}
for (int x : array) {
System.out.println(x);
}
在前面的文章中介绍过数组是引用数据类型,那其实数组并不会像基本数据类型中直接变量在栈开辟一块空间来直接存储值,而是在栈上开辟空间之后存储地址,如下图
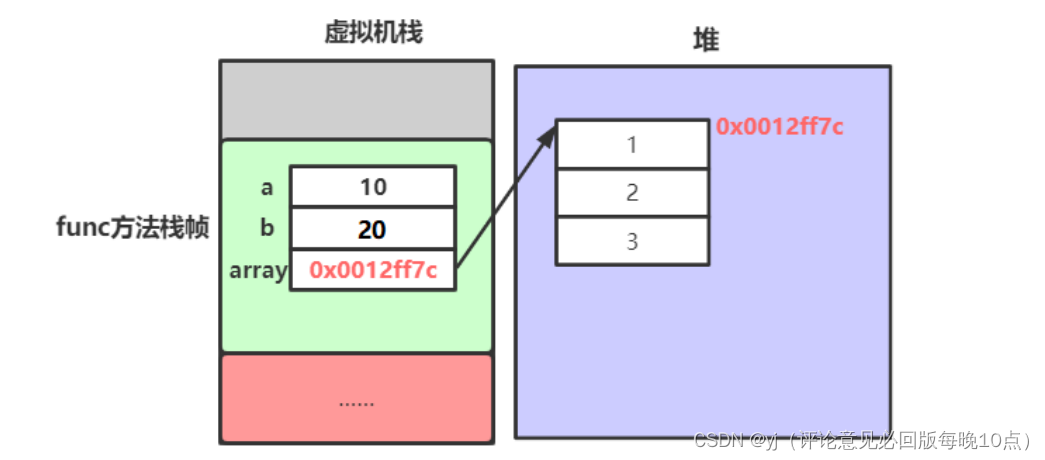
如此在数组作为参数传入方法时,那么实参和形参都指向堆上的同一片空间,对形参操作也会改变实参
二维数组
定义方式
类型[][] 数组名 = {{},{}};//中间的大括号不能省略在中间大括号中对对应行进行初始化
类型[][] 数组名 = new 类型[][]{{},{}};//中间的大括号不能省略在中间大括号中对对应行进行初始化
类型[][] 数组名 = new 类型[N][];//行数(N)不能省略,列可以省略
遍历方式
int[][] array = {{1,2,3},{4,5,6}};
for(int i = 0; i < array.length; i++){//array.length求出二维数组的行数
for(int j = 0; j < array[i].length; i++){//array[i].length求出二维数组当前行的列数
System.out.print("%d ", array[i][j]);
}
}
for(int[] ret : array){
for(int x : each){
System.out.print("%d ", array[i][j]);
}
}