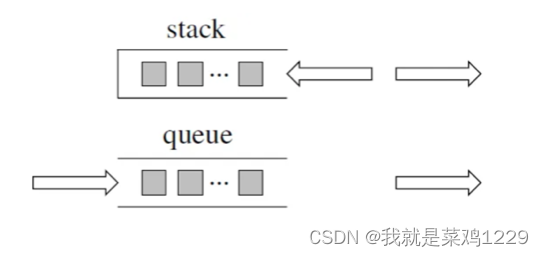
1.栈和队列理论基础

栈和队列的原理大家应该很熟悉了，队列是先进先出，栈是先进后出。

2.用栈实现队列

type MyQueue struct {
	head []int
	headSize int
	store []int
	storeSize int
}


func Constructor() MyQueue {
	return MyQueue{
		head : make([]int,100),
		headSize : 0,
		store : make([]int,100),
		storeSize : 0,
	}
}


func (this *MyQueue) Push(x int)  {
	this.store[this.storeSize] = x
	this.storeSize++
}


func (this *MyQueue) Pop() int {
	if this.headSize==0{
		//需要将store中的数倒过来
		for i:=this.storeSize;i>0;{
            i--
			this.head[this.headSize]=this.store[i]
            this.headSize++
		}
		this.storeSize = 0
	}
	if this.headSize>0{
		this.headSize--
		return  this.head[this.headSize]
	}
	return -1
}


func (this *MyQueue) Peek() int {
	if this.headSize==0{
		//需要将store中的数倒过来
		for i:=this.storeSize;i>0;{
            i--
			this.head[this.headSize]=this.store[i]
            this.headSize++
		}
		this.storeSize = 0
	}
	if this.headSize>0{
		return  this.head[this.headSize-1]
	}
	return -1
}


func (this *MyQueue) Empty() bool {
	return this.headSize==0&&this.storeSize==0
}

3.用队列实现栈

type MyStack struct {
    store []int
    size int
}

func remove(s []int, i int) []int {
    s[i] = s[len(s)-1]
    return s[:len(s)-1]
}

func Constructor() MyStack {
    return MyStack{make([]int,100),0}
}

func (this *MyStack) Push(x int)  {
    this.store[this.size]=x
    this.size++
}

func (this *MyStack) Pop() int {
    this.size--
    return this.store[this.size]
}

func (this *MyStack) Top() int {
    return this.store[this.size-1]
}

func (this *MyStack) Empty() bool {
    return this.size==0
}

4.有效的括号

func isValid(s string) bool {
	stack := Stack{}
	for i := 0; i < len(s); i++ {
		println(s[i])
		if s[i] == 40 || s[i] == 91 || s[i] == 123 {
			stack.Push(int(s[i]))
		} else {
			char, err := stack.Top()
			if err != nil {
				return false
			}
			if char == 40 && s[i] == 41 {
				stack.Pop()
				continue
			}
			if char == 91 && s[i] == 93 {
				stack.Pop()
				continue
			}
			if char == 123 && s[i] == 125 {
				stack.Pop()
				continue
			}
			return false
		}
	}
	if stack.Len() != 0 {
		return false
	}
	return true
}

type Stack []int

func (stack Stack) Len() int {
	return len(stack)
}

func (stack Stack) IsEmpty() bool {
	return len(stack) == 0
}

func (stack Stack) Cap() int {
	return cap(stack)
}

func (stack *Stack) Push(value int) {
	*stack = append(*stack, value)
}

func (stack Stack) Top() (int, error) {
	if len(stack) == 0 {
		return -1, errors.New("Out of index, len is 0")
	}
	return stack[len(stack)-1], nil
}

func (stack *Stack) Pop() (int, error) {
	theStack := *stack
	if len(theStack) == 0 {
		return -1, errors.New("Out of index, len is 0")
	}
	value := theStack[len(theStack)-1]
	*stack = theStack[:len(theStack)-1]
	return value, nil
}

5.删除字符串中的所有相邻重复项

func removeDuplicates(s string) string {
	chars := []byte(s)
	p1 := 0
	for i := 0; i < len(chars); i++ {
		if(p1>0 && chars[p1-1]==chars[i]){
			p1--
		}else{
			chars[p1] = chars[i]
			p1++
		}
	}
	return string(chars[:p1])
}

6.逆波兰表达式求值

func evalRPN(tokens []string) int {
    numIndex := -1
    numArr := make([]int,10000)
    for _,str := range(tokens){
        num, err := strconv.Atoi(str)
        if err==nil{
            //说明是数字
            numIndex++
            numArr[numIndex]=num
        }else{
            //说明是一个+-*/中的一种
            num1 := numArr[numIndex]
            numIndex--
            num2 := numArr[numIndex]
            switch str{
                case "+":
                    numArr[numIndex]=num1+num2
                case "-":
                    numArr[numIndex]=num2-num1
                case "*":
                    numArr[numIndex]=num1*num2
                case "/":
                    numArr[numIndex]=num2/num1
            }
        }
    }
    return numArr[0]
}

7.滑动窗口最大值

这道题目需要使用单调队列

// 封装单调队列的方式解题
// 那么这个维护元素单调递减的队列就叫做单调队列
// 即单调递减或单调递增的队列
type MyQueue struct {
	queue []int
}

func NewMyQueue() *MyQueue {
	return &MyQueue{
		queue: make([]int, 0),
	}
}

func (m *MyQueue) Front() int {
	return m.queue[0]
}

func (m *MyQueue) Back() int {
	return m.queue[len(m.queue)-1]
}

func (m *MyQueue) Empty() bool {
	return len(m.queue) == 0
}

// push(value)：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止
func (m *MyQueue) Push(val int) {
	for !m.Empty() && val > m.Back() {
		m.queue = m.queue[:len(m.queue)-1]
	}
	m.queue = append(m.queue, val)
}

// pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
func (m *MyQueue) Pop(val int) {
	if !m.Empty() && val == m.Front() {
		m.queue = m.queue[1:]
	}
}

func maxSlidingWindow(nums []int, k int) []int {
	queue := NewMyQueue()
	length := len(nums)
	res := make([]int, 0)
	// 先将前k个元素放入队列
	for i := 0; i < k; i++ {
		queue.Push(nums[i])
	}
	// 记录前k个元素的最大值
	res = append(res, queue.Front())
	for i := k; i < length; i++ {
		// 滑动窗口移除最前面的元素
		queue.Pop(nums[i-k])
		// 滑动窗口添加最后面的元素
		queue.Push(nums[i])
		// 记录最大值
		res = append(res, queue.Front())
	}
	return res
}

8.前K个高频元素

这题目需要实现go中提供的heap的接口。使用大顶堆即可完成任务。

func topKFrequent(nums []int, k int) []int {
	items := make(map[int]*Item, 0)
	for i := 0; i < len(nums); i++ {
		item, ok := items[nums[i]]
		if !ok {
			items[nums[i]] = &Item{key: nums[i], value: 1}
		} else {
			item.value++
		}
	}

	hp := &ItemHeap{}
	heap.Init(hp)
	for _, value := range items {
		heap.Push(hp, *value)
	}

	res := make([]int, k)
	for i := 0; i < k; i++ {
		item := heap.Pop(hp)
		res[i] = item.(Item).key
	}
	return res
}


//大顶堆
type Item struct {
	// 排序的关键词
	key int
	// value，用来记录出现的次数
	value int
}

type ItemHeap []Item

func (h ItemHeap) Len() int {
	return len(h)
}

func (h ItemHeap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}

func (h ItemHeap) Less(i, j int) bool {
	return h[i].value > h[j].value
}

// 实现heap.Interface接口定义的额外方法
func (h *ItemHeap) Push(item interface{}) {
	*h = append(*h, item.(Item))
}

// 这个方法不是给用户使用的
func (h *ItemHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}