模电·典型的静态工作点稳定电路

典型的静态工作点稳定电路

电路组成和Q点稳定原理
二、静态工作点估算
三、态参数的估算

电路组成和Q点稳定原理

典型的Q点稳定电路如下图1所示，图（a）为直接耦合方式，图（b）为阻容耦合方式，它们具有相同的直流通路，如图（c）所示。
静态工作点稳定电路

图1. 静态工作点稳定电路 （a）直接耦合电路（b）阻容耦合电路（c）图(a)、(b)所示电路的直流通路

在图1( c )所示电路中，节点B的电流方程为
$I{\tiny 2} = {I\tiny 1}+{I\tiny BQ}$
为了稳定Q点，通常使参数选取满足
${I\tiny 1}>>{I\tiny BQ}$
因此， ${I\tiny 2}≈{I\tiny 1}$ ，B点电位
${U\tiny BQ}≈\frac{R\tiny b1}{{R\tiny b1}+{R\tiny b2}}*{V\tiny CC}$
上式表明基极电位几乎仅决定于 $R\tiny b1$ 与 $R\tiny b2$ ，对 $V\tiny CC$ 的分压，而与环境温度无关，即当温度变化时 $U\tiny BQ$ 基本不变。
当温度升高时，集电极电流 $I\tiny C$ 增大，发射极电流 $I\tiny E$ 必然相应增大，因而发射极电阻 $R\tiny e$ 上的电压 $U\tiny E$ (即发射极的电位)随之增大；因为 $U\tiny BQ$ 基本不变，而 ${U\tiny BE}={U\tiny B}-{U\tiny E}$ ，所以 $U\tiny BE$ 势必减小，导致基极电流 $I\tiny B$ 减小， $I\tiny C$ 随之相应减小。结果， $I\tiny C$ 随温度升高而增大的部分几乎被由于 $I\tiny B$ 减小而减小的部分相抵消， $I\tiny C$ 将基本不变， $U\tiny CE$ 也将基本不变，从而Q点在晶体管输出特性坐标平面上的位置基本不变。可将上述过程简写为:
在这里插入图片描述
当温度降低时，各物理量向相反方向变化， $I\tiny C$ 和 $U\tiny CE$ 也将基本不变。
不难看出，在稳定的过程中， $R\tiny e$ 起着重要作用，当晶体管的输出回路电流 $I\tiny C$ 变化时，通过 $R\tiny e$ 上产生电压的变化来影响b - e间电压，从而使 $I\tiny B$ 向相反方向变化，达到稳定Q点的目的。这种将输出量（ $I\tiny C$ ）通过一定的方式（利用 $R\tiny e$ 将 $I\tiny C$ 的变化转化成电压的变化）引回到输入回路来影响输入量（ $U\tiny BE$ ）的措施称为反馈；由于反馈的结果使输出量的变化减小，故称为负反馈；又由于反馈出现在直流通路之中，故称为直流负反馈。 $R\tiny e$ 为直流负反馈电阻。
由此可见，上图1.（c）所示电路Q点稳定的原因是:
（1） $R\tiny e$ 的直流负反馈作用;
（2）在 ${I\tiny 1}>>{I\tiny BQ}$ 的情况下， ${U\tiny BQ}$ 在温度变化时基本不变。
所以也称这种电路为分压式电流负反馈Q点稳定电路。从理论上讲， $R\tiny e$ 越大，反馈越强，Q点越稳定。但是实际上，对于一定的集电极电流 $I\tiny C$ ，由于 $V\tiny CC$ 的限制， $R\tiny e$ 太大会使晶体管进入饱和区，电路将不能正常工作。

二、静态工作点估算

已知 ${I\tiny 1}>>{I\tiny BQ}$
${U\tiny BQ}≈\frac{R\tiny b1}{{R\tiny b1}+{R\tiny b2}}*{V\tiny CC}$
发射极电流
${I\tiny EQ}=\frac{{U\tiny BQ}-{U\tiny BEQ}}{R\tiny e}$
由于 ${I\tiny CQ}≈{I\tiny EQ}$ ，管压降
${U\tiny CEQ}≈{V\tiny CC}-{I\tiny CQ}({R\tiny c}+{R\tiny e})$
基极电流
${I\tiny BQ}=\frac{I\tiny EQ}{1+{\beta}}$
应当指出，不管电路参数是否满足 ${I\tiny 1}>>{I\tiny BQ}$ ， $R\tiny w$ 的负反馈作用都存在。利用戴维南定理，可将上图1.静态工作点稳定电路中（C）所示电路变换成下图2.所示电路
在这里插入图片描述

图2. 图1电路中(c)所示电路的等效电路

其中
${V\tiny BB}=\frac{R\tiny b1}{{R\tiny b1}+{R\tiny b2}}*{V\tiny CC}$ ${R\tiny b}={R\tiny b1}//{R\tiny b2}$
列输入回路方程
${V\tiny BB}={I\tiny BQ}{R\tiny b}+{U\tiny BEQ}+{I\tiny EQ}{R\tiny e}$
可得出 $I\tiny EQ$
${I\tiny EQ}=\frac{{V\tiny BB}-{U\tiny BEQ}}{{\frac{R\tiny b}{1+{\beta}}+{R\tiny e}}}$
当 ${R\tiny e}>>{\frac{R\tiny b}{1+{\beta}}}$ ，即 $(1+{\beta}){R\tiny e}>>{R\tiny b}$ 时， ${I\tiny EQ}$ 的表达式与 ${I\tiny EQ}=\frac{{U\tiny BQ}-{U\tiny BEQ}}{R\tiny e}$ 相同。因此，可用 $(1+{\beta}){R\tiny e}$ 与 ${R\tiny b1}//{R\tiny b2}$ 的大小关系来判断 ${I\tiny 1}>>{I\tiny BQ}$ 是否成立。

三、态参数的估算

静态工作点稳定电路

图1. 静态工作点稳定电路 （a）直接耦合电路（b）阻容耦合电路（c）图(a)、(b)所示电路的直流通路

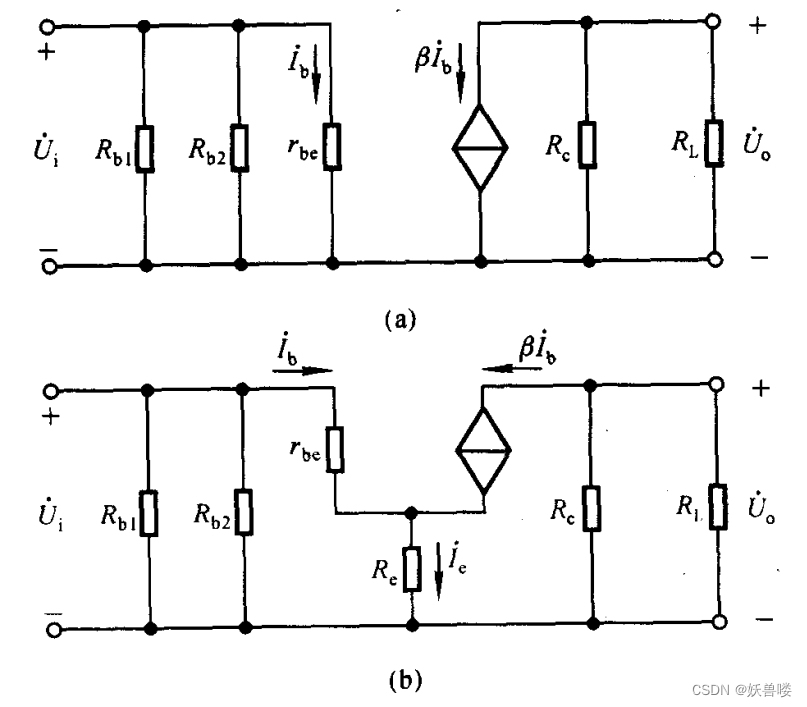
在这里插入图片描述

图3. 阻容耦合Q点稳定电路的交流等效电路 （a）有旁路电容时的交流等效电路（b）无旁路电容时的交流等效电路$

图1.静态工作点稳定电路中（b）所示的交流等效电路，如图3.阻容耦合Q点稳定电路的交流等效电路中（a）所示，电容 $C\tiny e$ 为旁路电容，容量很大，对交流信号可视为短路。若将 ${R\tiny b1}//{R\tiny b2}$ 看成一个电阻 $R\tiny b$ ，则图3.阻容耦合Q点稳定电路的交流等效电路所示电路（a）与阻容耦合共射放大电路的交流等效电路(见图4)完全相同，
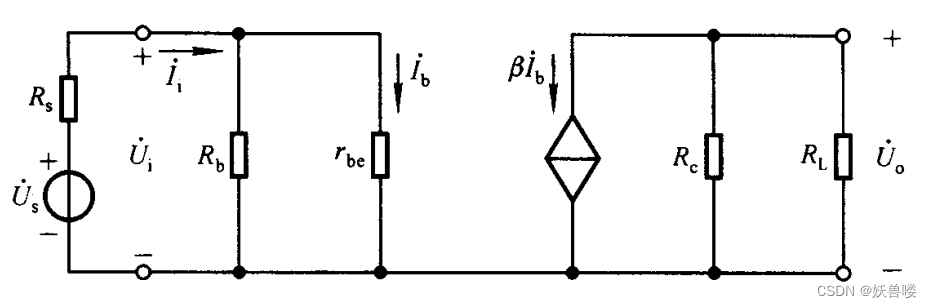
在这里插入图片描述

图4. 阻容耦合共射放大电路的交流等效电路

因此动态参数
$\begin{cases} \.{A}{\tiny u}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=-\frac{{\beta}{R'\tiny L}}{{\large r}{\tiny be}} （{R'\tiny L}={R\tiny c}//{R\tiny L}）\\ \\ {R\tiny i}=\frac{\.U\tiny i}{\.I\tiny i}={R\tiny b}//{\large r\tiny be}={R\tiny b1}//{R\tiny b2}//{\large r\tiny be}\\ \\ {R\tiny o}={R\tiny c} \end{cases}$
倘若没有旁路电容 $C\tiny e$ ，则图1.静态工作点稳定电路中图（b）所示电路的交流等效电路如图3.阻容耦合Q点稳定电路的交流等效电路中（b）所示。由图可知
$\.U{\tiny i}=\.I{\tiny b}{\large r}{\tiny be}+\.I{\tiny e}{R\tiny e}=\.I{\tiny b}{\large r}{\tiny e}+\.I{\tiny b}(1+\beta){R\tiny e}$ $\.U{\tiny o}=-\.I{\tiny c}R'{\tiny L}$
所以
$\begin{cases} \.{A}{\tiny u}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=-\frac{{\beta}{R'\tiny L}}{{\large r}{\tiny be}+(1+\beta){R \tiny e}} （{R'\tiny L}={R\tiny c}//{R\tiny L}）\\ \\ {R\tiny i}=\frac{\.U\tiny i}{\.I\tiny i}={R\tiny b1}//{R\tiny b2}//[{\large r\tiny be}+(1+\beta){R\tiny e}]\\ \\ {R\tiny o}={R\tiny c} \end{cases}$
在式 $\.{A}{\tiny u}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=-\frac{{\beta}{R'\tiny L}}{{\large r}{\tiny be}+(1+\beta){R \tiny e}} （{R'\tiny L}={R\tiny c}//{R\tiny L})$ 中
若 $(1+\beta){R\tiny e}>>{\large r}{\tiny be}$ ，且 $\beta >>1$ ，则
$\.A{\tiny u}=\frac{\.U{\tiny o}}{\.U{\tiny i}}≈-\frac{R'{\tiny L}}{R{\tiny e}}\ （R'{\tiny L}={R\tiny c}//{R\tiny L}）$
可见，虽然 $R\tiny e$ 使 $|\.A{\tiny u}|$ 减小了，但由于 $\.A{\tiny u}$ 仅决定于电阻取值，不受环境温度的影响，所以温度稳定性好。

【例】在图1. (b)所示电路中，已知 ${V\tiny CC}=12V$ ， ${R\tiny b1}=5kΩ$ ， ${R\tiny b2}=15kΩ$ ， ${R\tiny e}=2.3kΩ$ ， ${R\tiny e}=5.1kΩ$ ， ${R\tiny L}=5.1kΩ$ ；晶体管的 $\beta =50$ ， ${\large r\tiny be}=1.5kΩ$ ， ${U\tiny BEQ}=0.7 V$ 。
（1）估算静态工作点Q;
（2）分别求出有、无 $C\tiny e$ 两种情况下的 $\.A\tiny u$ 和 $R\tiny i$ 。
（3）若 $R\tiny b1$ 因虚焊而开路，则电路会产生什么现象?
解:
（1）求解Q点，因为 $(1+\beta){R\tiny e}>>{R\tiny b1}//{R\tiny b2}$ ，所以
${U\tiny BQ}≈\frac{R\tiny b1}{{R\tiny b1}+{R\tiny b2}}*{V\tiny CC}=(\frac{5}{5+15}*12)V=3V$

${I\tiny EQ}=\frac{{U\tiny BQ}-{U\tiny BEQ}}{{R\tiny e}}≈(\frac{3-0.7}{2.3})mA=1mA$

${U\tiny CEQ}≈{V\tiny CC}-{I\tiny CQ}({R\tiny c}+{R\tiny e})=[12-1*(5.1+2.3)]V=4.6V$

${I\tiny BQ}=\frac{{\small I\tiny EQ}}{{1+\beta}}=(\frac{1}{1+50})mA≈0.02=20μA$

(2）求解 $\.A\tiny u$ 和 $R\tiny i$ 。
当有 $C\tiny e$ 时:
$\.A{\tiny u}=-\frac{\small{\beta R'}{\tiny L}}{\large r{\tiny be}}=-\frac{50*\frac{5.1*5.1}{5.1+5.1}}{1.5}=-85$ ${R\tiny i}={R\tiny b1}//{R\tiny b2}//{r\tiny be}≈1.07kΩ$
当无 $C\tiny e$ 时，由于 $(1+\beta){R\tiny e}>>{r\tiny be}$ ，且 $\beta >>1$ ，所以
$\.A{\tiny u}≈-\frac{\small R'\tiny L}{R\tiny e}=-1.7$ ${R\tiny i}={R\tiny b1}//{R\tiny b2}//[{r\tiny be}+(1+\beta){R\tiny e}]≈3.75kΩ$
当无 $C\tiny e$ 时，电路的电压放大能力很差，因此在实用电路中常常将 $R\tiny e$ 分为两部分，只将其中一部分接旁路电容。
(3）若 $R\tiny b1$ 开路，则电路如下图5.所示。设电路中晶体管仍工作在放大状态，则基极电流和集电极电流(也约为发射极电流)分别为
${I\tiny BQ}=\frac{{V\tiny CC}-{U\tiny BEQ}}{{R\tiny b2}+(1+\beta){R\tiny e}}=[\frac{12-0.7}{15+(1+50)*2.3}]mA=0.09mA$ ${I\tiny CQ}={\beta I\tiny BQ}=(50*0.09)mA=4.5mA$
管压降
${U\tiny CEQ}≈{V\tiny CC}-{I\tiny CQ}({R\tiny c}+{R\tiny e})=[12-4.5*(5.1+2.3)]V=-21.3V$
上式表明，原假设不成立，管子已不工作在放大区，而进入饱和区，动态分析已无意义。
若晶体管的饱和管压降 ${U\tiny CES}={U\tiny BEQ}=0.7V$ ，则管子的发射极电位和集电极电位分别近似为
${U\tiny EQ}=\frac{{V\tiny CC}-{U\tiny CES}}{{R\tiny c}+{R\tiny e}}*{R\tiny e}=(\frac{12-0.7}{5.1+2.3}*2.3)V=3.52V$ ${U\tiny CQ}={U\tiny EQ}+{U\tiny CES}=(3.52+0.7)V=4.22V$
本题也可假设晶体管工作在饱和区，然后通过分析来判断假设的正确性。