🌈个人主页：努力学编程’
⛅个人推荐：基于java提供的ArrayList实现的扑克牌游戏 |C贪吃蛇详解
⚡学好数据结构，刷题刻不容缓：点击一起刷题
🌙心灵鸡汤：总有人要赢，为什么不能是我呢

🌈二叉搜索树

二叉搜索树又称二叉排序树，从节点的个数上又可分为两种，空树或者具有一定性质的树，这种具有特殊性质的树具有特点：

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

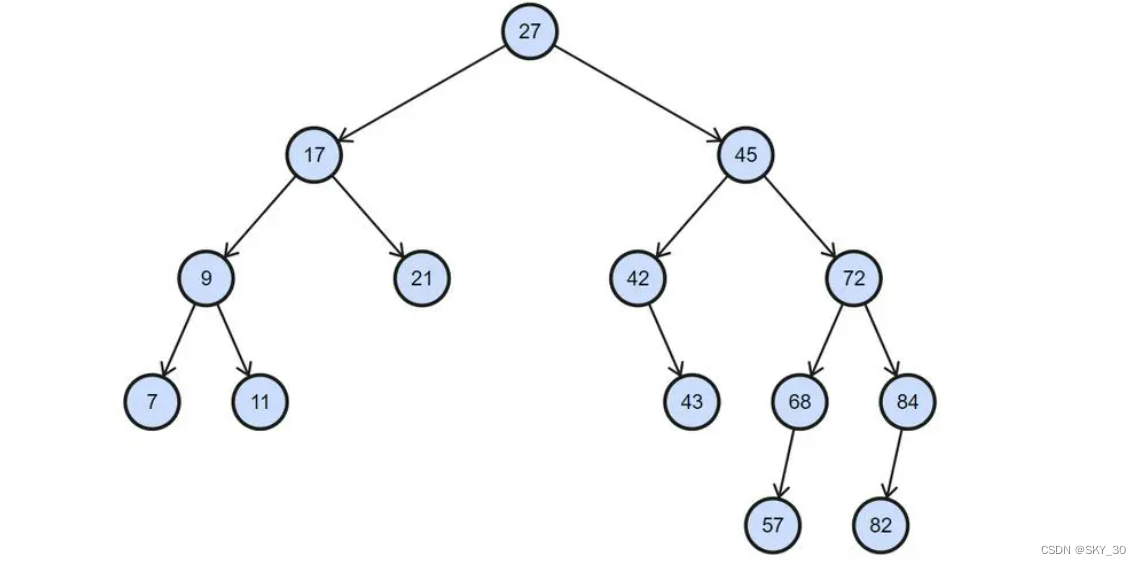
根节点27的左子树的所有的节点的值都小于27，右子树的所有节点的值都大于27，这也是为什么我们叫他二叉排序树的原因。当然他的每个子树也都满足这个性质。

⚡⚡⚡特别说明：当我们使用中序遍历搜索二叉树的时候，遍历所得的数组是一个有序数组。

🌈二叉搜索树-查找

如何在二叉搜索树中查找数值呢，他和普通二叉树有区别吗？

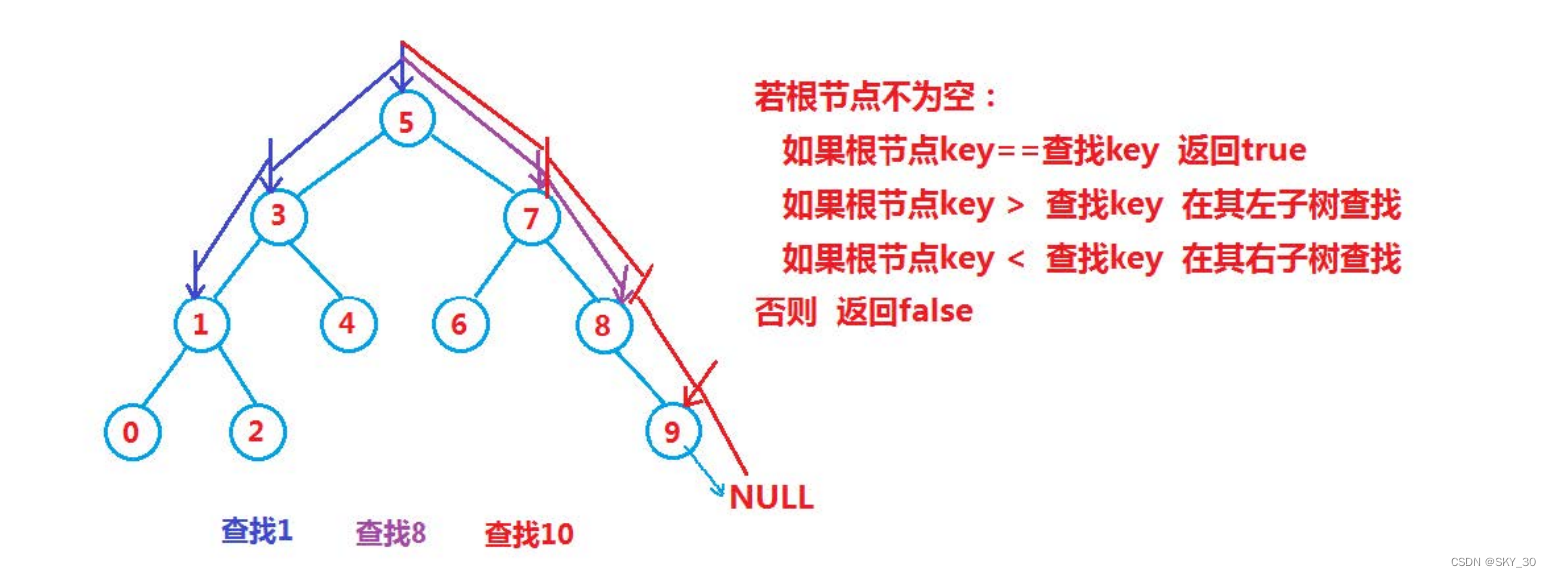
• 当然我们在查找索索二叉树数值的时候，我们理应利用它结构上的特点进行查找：
• 节点为空： 返回fasle；
• 节点不为空：Key>root.val 在根节点的右侧进行查找
• 节点不为空： Key<root.val 在根节点的左侧进行查找

🌈二叉搜索树-插入

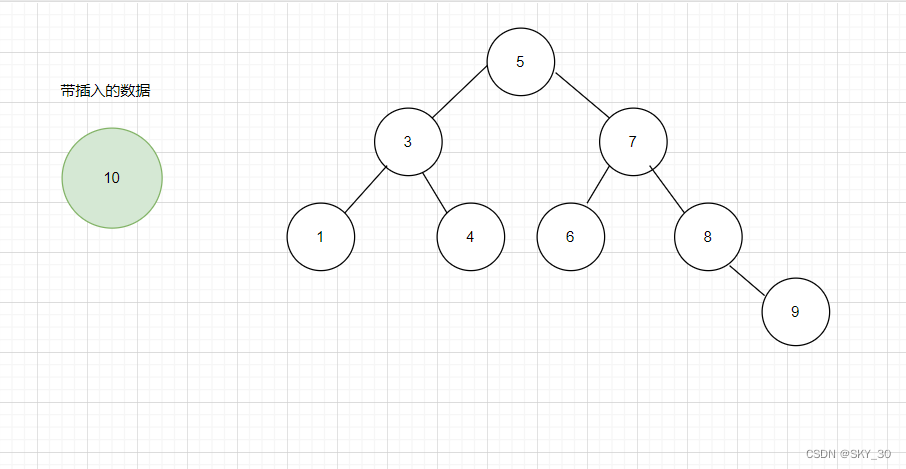
在二叉搜索树当中，插入数据分为两步：找到要插入数据的位置，插入数据。

• 如何找到插入数据的位置是最重要的一步，其实这步和查找有一定的相似度。我们将带插入数据与当前的根节点进行比较，根据大小关系，在树的左右子树进行查找。

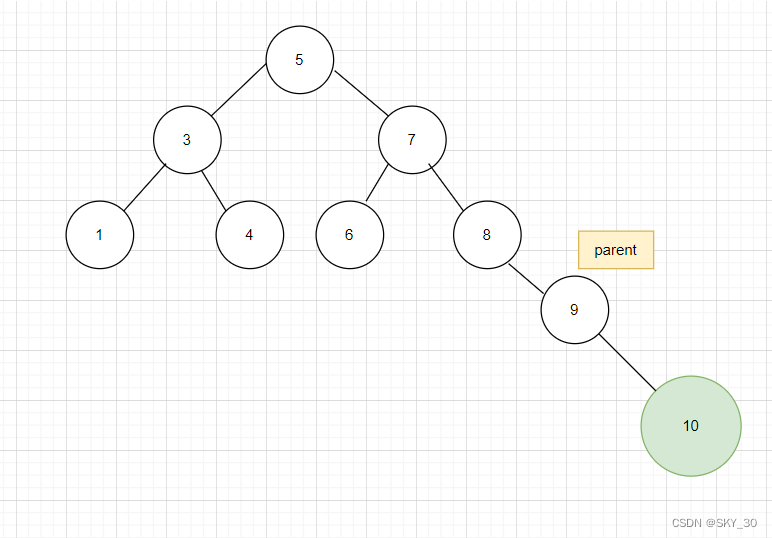
• 直到找到我们需要插入点的位置，但是只要你实际操作这个过程就会发现我们无法直接定位到需要插入数据的位置，只能定位到带插入位置的下个一位置，所以我们需要创建一个指针定位到插入数据指针的上一个位置，这样就找到了待插入的位置.

• 若节点为空，直接插入节点！！！

• 使用parent标记带插入的位置，直接进行插入：
  

🌈二叉搜索树-删除

对于删除操作，比较麻烦，需要分不同的几种情况进行讨论，待删除的节点cur，待删除的数据的父节点parent：

• cur.left == null:

• cur 是 root: 则 root = cur.right

• cur 不是 root，cur 是 parent.left: 则 parent.left = cur.right

• cur 不是 root，cur 是 parent.right 则 parent.left = cur.left

• cur.right==null:

• cur是root： 则 则 root = cur.left

• cur 不是 root，cur 是 parent.left，则 parent.left = cur.left

• cur 不是 root，cur 是 parent.right，则 parent.right = cur.left

• cur.left != null && cur.right != null:

• 需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被
  删除节点中，再来处理该结点的删除问题

🌈搜索二叉树-模拟实现：

针对于搜索二叉树的增删查改的基础操作代码的实现：

public class BinarySearchTree {
    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public TreeNode root = null;

    public TreeNode search(int key) {
        TreeNode cur = root;
        while (cur != null) {
            if(cur.val < key) {
                cur = cur.right;
            }else if(cur.val > key) {
                cur = cur.left;
            }else {
                return cur;
            }
        }
        return null;
    }

    public void insert(int val) {
        TreeNode node = new TreeNode(val);
        if(root == null) {
            root = node;
            return;
        }
        TreeNode cur = root;
        TreeNode parent = null;
        while (cur != null) {
            if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            }else if(cur.val > val) {
                parent = cur;
                cur = cur.left;
            }else {
                return;
            }
        }
        //parent 指向的节点 就是 需要插入的节点位置 的 父亲节点
        if(parent.val > val) {
            parent.left = node;
        }else {
            parent.right = node;
        }
    }
    //key = 10;
    public void remove(int key) {
        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {
            if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else if(cur.val > key) {
                parent = cur ;
                cur = cur.left;
            }else {
                removeNode(parent,cur);
                return;
            }
        }
    }
    private void removeNode(TreeNode parent,TreeNode cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            TreeNode target = cur.right;
            TreeNode targetP = cur;
            while (target.left != null) {
                targetP = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetP.left) {
                targetP.left = target.right;
            }else {
                targetP.right = target.right;
            }
        }
    }
}

🌈二叉搜索树-算法性能分析

针对我们上面的基础操作，插入和删除都需要查找操作，针对二叉树的查找，我们需要根据树的结构进行分析，不同的结构时间复杂度也会不同。

⚡⚡⚡完全二叉树
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：$logN$

💧💧💧右单支
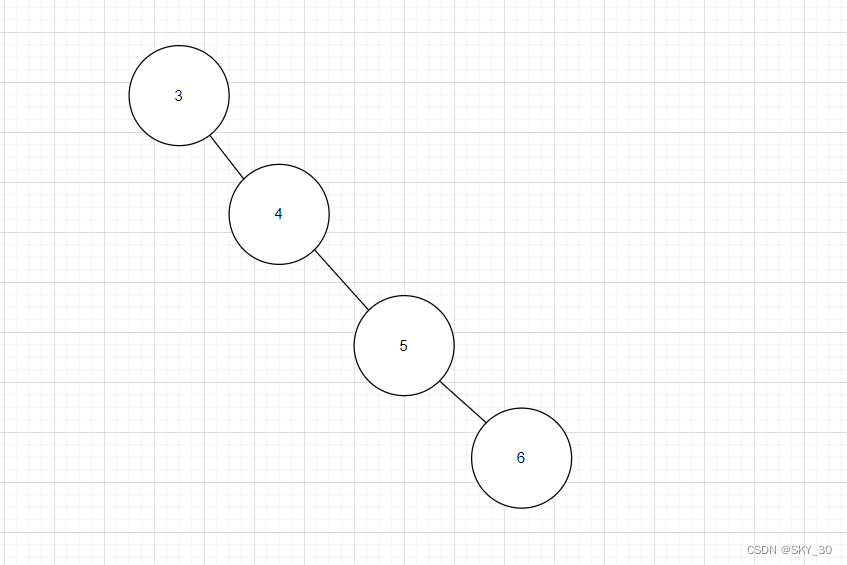
最差情况下，二叉搜索树退化为单支树，其平均比较次数为：2/N

🌈二叉搜索树-力扣刷题

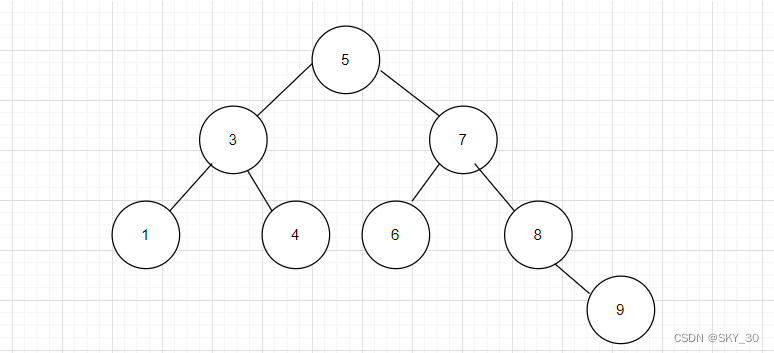
解题思路：我们解决二叉树问题，优先思考的是利用递归的套路解决问题，由于这是一颗搜索二叉树，我们也应当利用树的特点，解决这个问题：

递归的套路：

• 方法的返回值和参数
• 递归结束的条件
• 单层遍历
• 结合搜索二叉树的性质解决问题

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
         if(root==null||root.val==val) return root;
         TreeNode result=null;
         if(root.val>val) result=searchBST(root.left,val);
         if(root.val<val) result=searchBST(root.right,val);
         return result;
    }
}

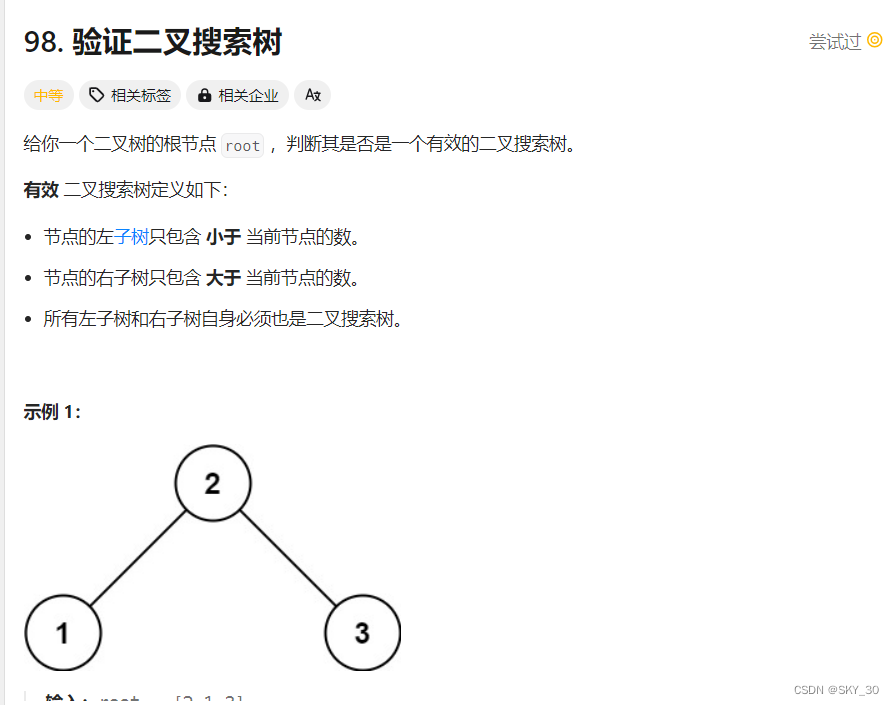
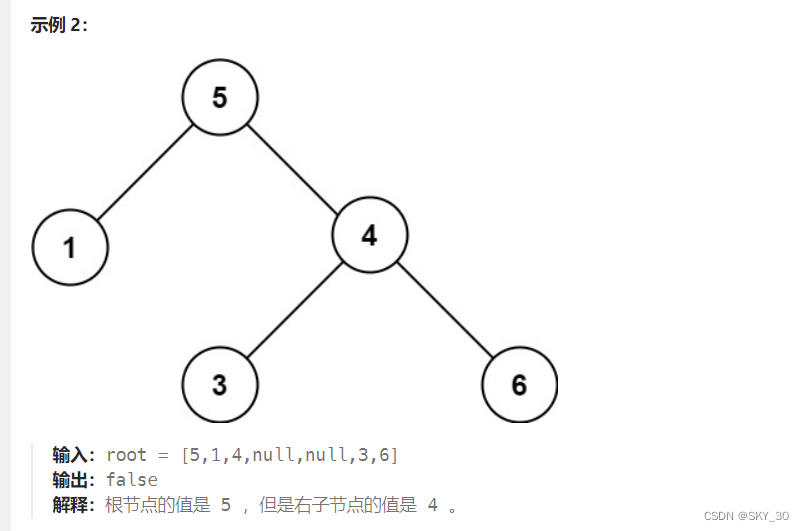
解题思路：是否是一颗搜索二叉树，应当使用其定义进行判断，左子树必须小于根节点的值，右子树所有的节点必须大于根节点的值。当然他的每一棵子树都必须满足这个特性。

那么我们就可以利用递归实现这个过程，
所以递归的方法的返回值:首先是boolean ，参数是根节点，左右节点，
结束条件：root==null return true;
if(node.val<=lower||node.val>=upper) return false;
单层遍历：validBST(lower, root.val, root.left) && validBST(root.val, upper, root.right);

class Solution {
    public boolean isValidBST(TreeNode root) {
        return validBST(Long.MIN_VALUE, Long.MAX_VALUE, root);
    }
    boolean validBST(long lower, long upper, TreeNode root) {
        if (root == null) return true;
        if (root.val <= lower || root.val >= upper) return false;
        return validBST(lower, root.val, root.left) && validBST(root.val, upper, root.right);
    }
}