Offer必备算法37_记忆化搜索_五道力扣题详解（由易到难）

news2024/11/19 0:48:35

目录

记忆化搜索概念和使用场景

①力扣509. 斐波那契数

解析代码1_循环

解析代码2_暴搜递归

解析代码3_记忆化搜索

解析代码4_动态规划

②力扣62. 不同路径

解析代码1_暴搜递归（超时）

解析代码2_记忆化搜索

解析代码3_动态规划

③力扣300. 最长递增子序列

解析代码1_爆搜递归（超时）

解析代码2_记忆化搜索

解析代码3_动态规划

④力扣375. 猜数字大小 II

解析代码1_爆搜递归（超时）

解析代码2_记忆化搜索

⑤力扣329. 矩阵中的最长递增路径

解析代码1_爆搜递归（超时）

解析代码2_记忆化搜索

本篇完。

记忆化搜索概念和使用场景

记忆化搜索是一种典型的空间换时间的思想，可以看成带备忘录的爆搜递归。

        搜索的低效在于没有能够很好地处理重叠子问题。在搜索过程中，会有很多重复计算，如果我们能记录一些状态的答案，就可以减少重复搜索量。动态规划虽然比较好地处理了重叠子问题，但是在有些拓扑关系比较复杂的题目面前，又显得无奈。记忆化搜索正是在这样的情况下产生的，它采用搜索的形式和动态规划中递推的思想将这两种方法有机地综合在一起，扬长避短，简单实用，在信息学中有着重要的作用。

        根据记忆化搜索的思想，它是解决重复计算，而不是重复生成，也就是说，这些搜索必须是在搜索扩展路径的过程中分步计算的题目，也就是“搜索答案与路径相关″的题目，而不能是搜索一个路径之后才能进行计算的题目，必须要分步计算，并且搜索过程中，一个搜索结果必须可以建立在同类型问题的结果上，也就是类似于动态规划解决的那种。

        记忆化搜索的典型应用场景是可能经过不同路径转移到相同状态的dfs问题。更明确地说，当我们需要在有层次结构的图（不是树，即当前层的不同节点可能转移到下一层的相同节点）中自上而下地进行dfs搜索时，大概率我们都可以通过记忆化搜索的技巧降低时间复杂度。

动态规划和记忆化搜索都是在爆搜的基础上优化。《算法导论》里也把记忆化搜索看成动态规划。

①力扣509. 斐波那契数

509. 斐波那契数

难度 简单

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

  • 0 <= n <= 30
class Solution {
public:
    int fib(int n) {

    }
};

解析代码1_循环

求斐波那契数是很经典的一道题，有多种解法。

        下面会从递归解法得出记忆化搜索解法，在得出动态规划解法，循环的解法也可以看作动态规划的状态压缩，完成闭环。

class Solution {
public:
    int fib(int n) {
        if (n < 2)
            return n;
        int fib1 = 0, fib2 = 0, ret = 1;
        for (int i = 2; i <= n; ++i)
        {
            fib1 = fib2;
            fib2 = ret;
            ret = fib1 + fib2;
        }
        return ret;
    }
};

解析代码2_暴搜递归

暴搜递归：

  • 递归含义：给 dfs 一个使命，给它一个数 n ，返回第 n 个斐波那契数的值。
  • 函数体：斐波那契数的递推公式。
  • 递归出口：当 n == 0 或者 n == 1 时，不用套公式。
class Solution {
public:
    int fib(int n) {
        return dfs(n);
    }

    int dfs(int n)
    {
        if(n <= 1)
            return n;
        return dfs(n - 1) + dfs(n - 2);
    }
};

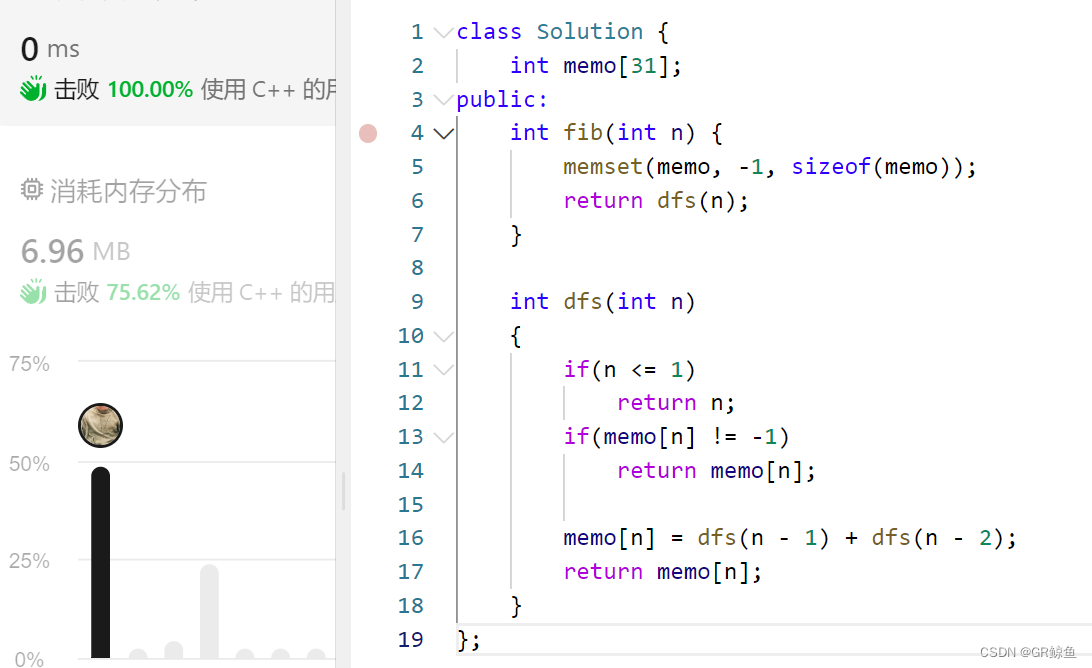
解析代码3_记忆化搜索

记忆化搜索：

  • 在递归的基础上加上一个备忘录（所以记忆化搜索也叫带备忘录的递归）。
  • 每次进入递归的时候，去备忘录里面看看。
  • 每次返回的时候，将结果加入到备忘录里面。
class Solution {
    int memo[31];
public:
    int fib(int n) {
        memset(memo, -1, sizeof(memo));
        return dfs(n);
    }

    int dfs(int n)
    {
        if(n <= 1)
            return n;
        if(memo[n] != -1)
            return memo[n];

        memo[n] = dfs(n - 1) + dfs(n - 2);
        return memo[n];
    }
};

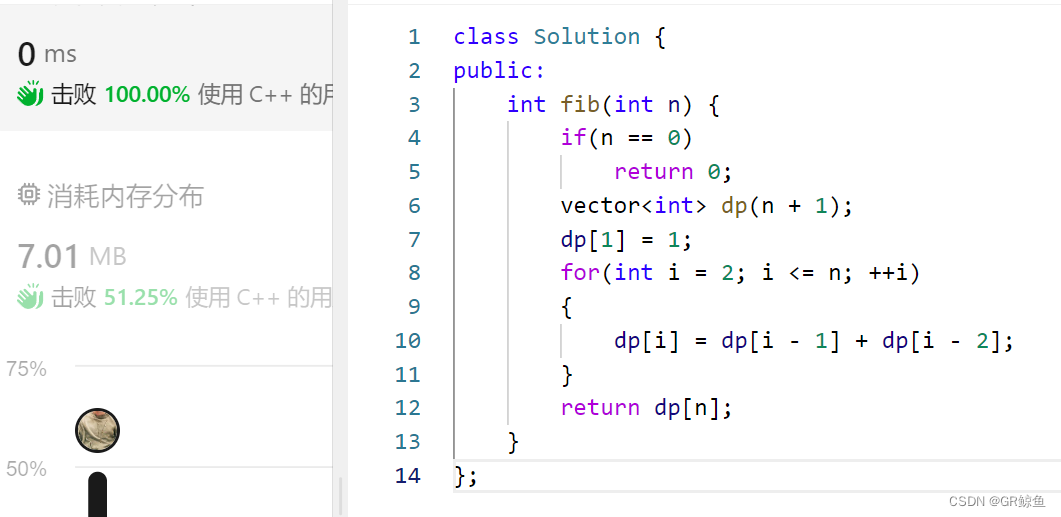
解析代码4_动态规划

动态规划已经写过很多题了，这里根据记忆化搜索得出动态规划的解法：

  • 递归含义：状态表示
  • 函数体：状态转移方程
  • 递归出口：初始化
  • 填表顺序：填备忘录的顺序
  • 返回值：备忘录的值

        可以看出都是类似的，因为两者本质都是一样的，都是在爆搜的基础上优化。《算法导论》里也把记忆化搜索看成动态规划。

        所以很多时候都可以把爆搜递归的代码改成记忆化搜索，再改成动态规划，不过爆搜改记忆化搜索已经完成时间的优化了，没太多必要改成动态规划了。

class Solution {
public:
    int fib(int n) {
        if(n == 0)
            return 0;
        vector<int> dp(n + 1);
        dp[1] = 1;
        for(int i = 2; i <= n; ++i)
        {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

②力扣62. 不同路径

62. 不同路径

难度 中等

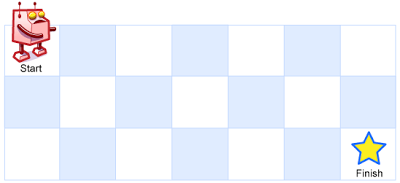
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

  • 1 <= m, n <= 100
  • 题目数据保证答案小于等于 2 * 10^9
class Solution {
public:
    int uniquePaths(int m, int n) {

    }
};

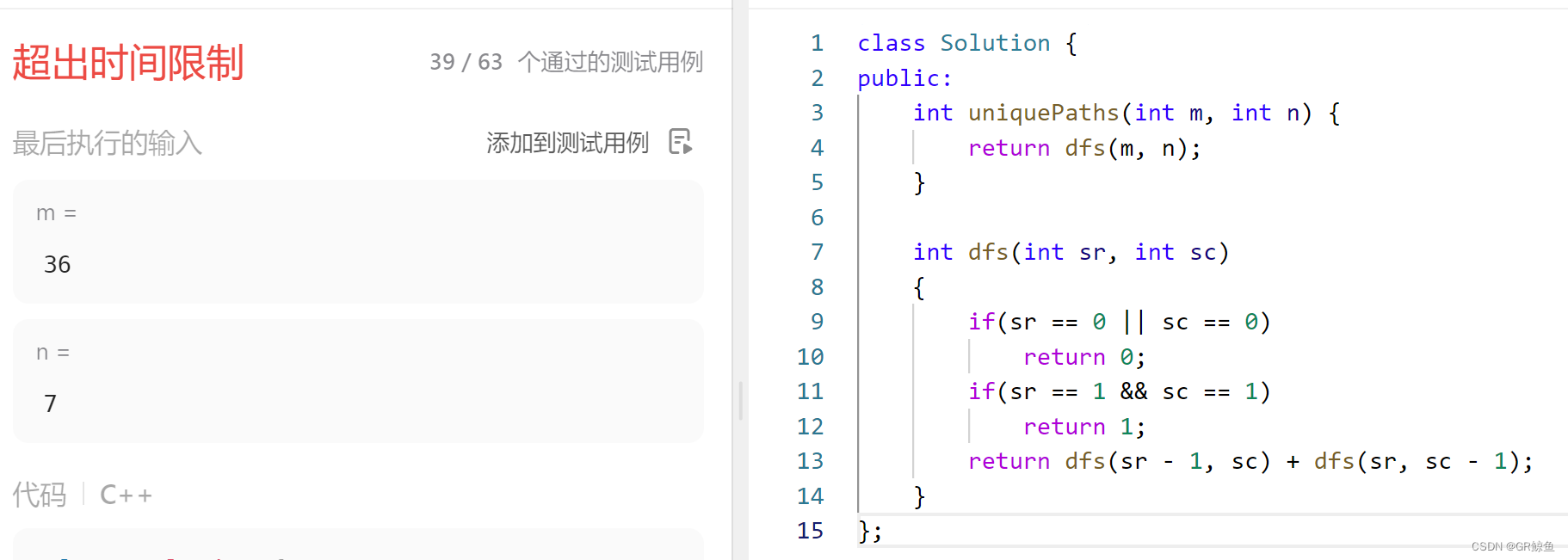
解析代码1_暴搜递归（超时）

  • 递归含义：给 dfs 一个下标，返回从 [0, 0] 位置走到 [i, j] 位置一共有多少种方法。
  • 函数体：只要知道到达上面位置的方法数以及到达左边位置的方法数，然后累加起来即可。
  • 递归出口：当下标越界的时候返回 0 ，当位于起点的时候，返回 1 。
class Solution {
public:
    int uniquePaths(int m, int n) {
        return dfs(m, n);
    }

    int dfs(int sr, int sc)
    {
        if(sr == 0 || sc == 0)
            return 0;
        if(sr == 1 && sc == 1)
            return 1;
        return dfs(sr - 1, sc) + dfs(sr, sc - 1);
    }
};

解析代码2_记忆化搜索

记忆化搜索解法：

  • 加上一个备忘录。
  • 每次进入递归的时候，去备忘录里面看看。
  • 每次返回的时候，将结果加入到备忘录里面。
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> memo(m + 1, vector<int>(n + 1));
        return dfs(m, n, memo);
    }

    int dfs(int sr, int sc, vector<vector<int>>& memo)
    {
        if(sr == 0 || sc == 0)
            return 0;
        if(sr == 1 && sc == 1)
            return 1;

        if(memo[sr][sc] != 0)
            return memo[sr][sc];
        
        memo[sr][sc] = dfs(sr - 1, sc, memo) + dfs(sr, sc - 1, memo);
        return memo[sr][sc];
    }
};

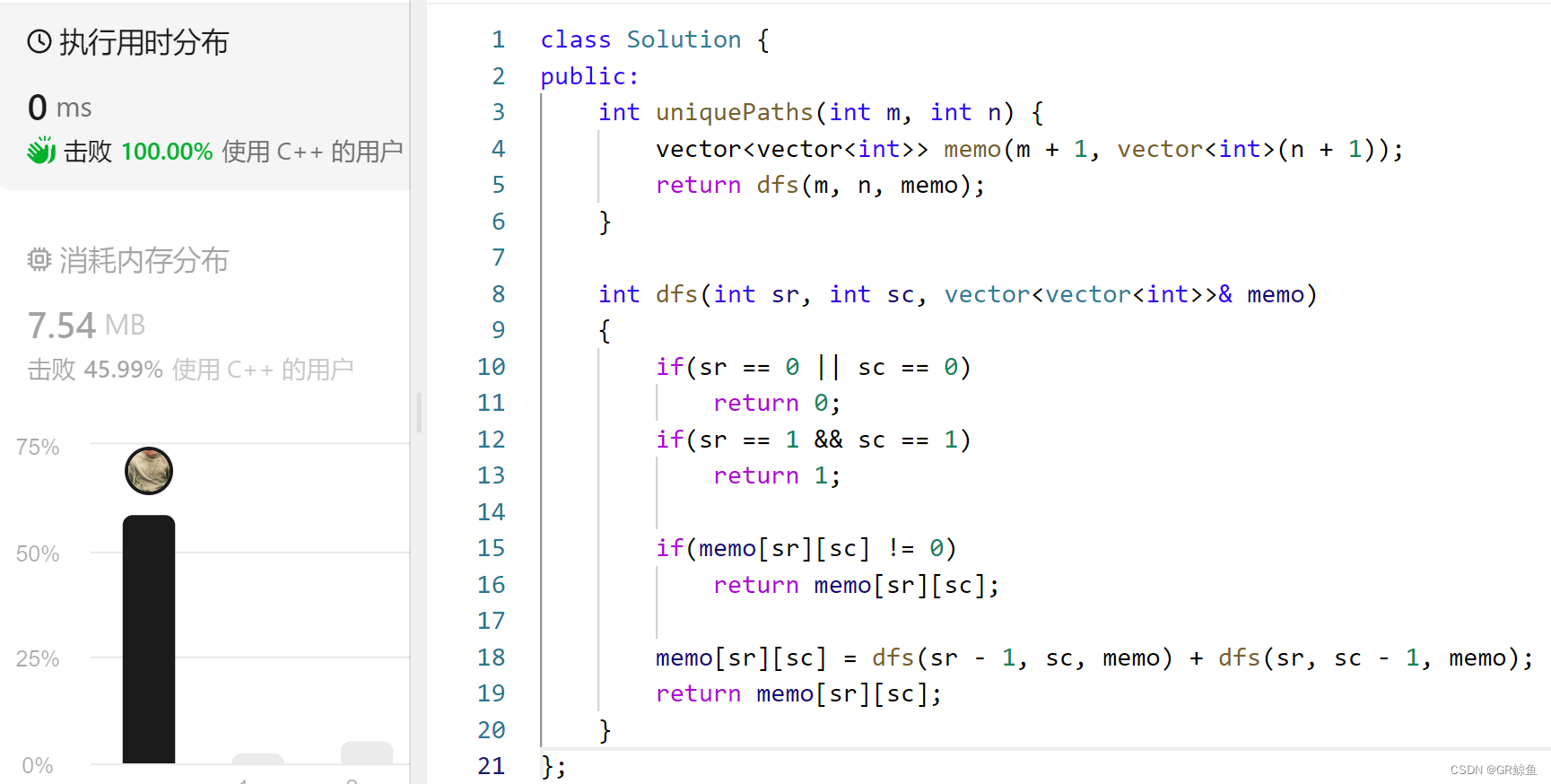
解析代码3_动态规划

根据记忆化搜索得出动态规划的解法：

  • 递归含义：状态表示
  • 函数体：状态转移方程
  • 递归出口：初始化
  • 填表顺序：填备忘录的顺序
  • 返回值：备忘录的值
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        dp[1][1] = 1;
        for(int i = 1; i <= m; ++i)
        {
            for(int j = 1; j <= n; ++j)
            {
                if(i == 1 && j == 1)
                    continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m][n];
    }
};

③力扣300. 最长递增子序列

300. 最长递增子序列

难度 中等

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

  • 1 <= nums.length <= 2500
  • -10^4 <= nums[i] <= 10^4

进阶：

  • 你能将算法的时间复杂度降低到 O(n log(n)) 吗?
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {

    }
};

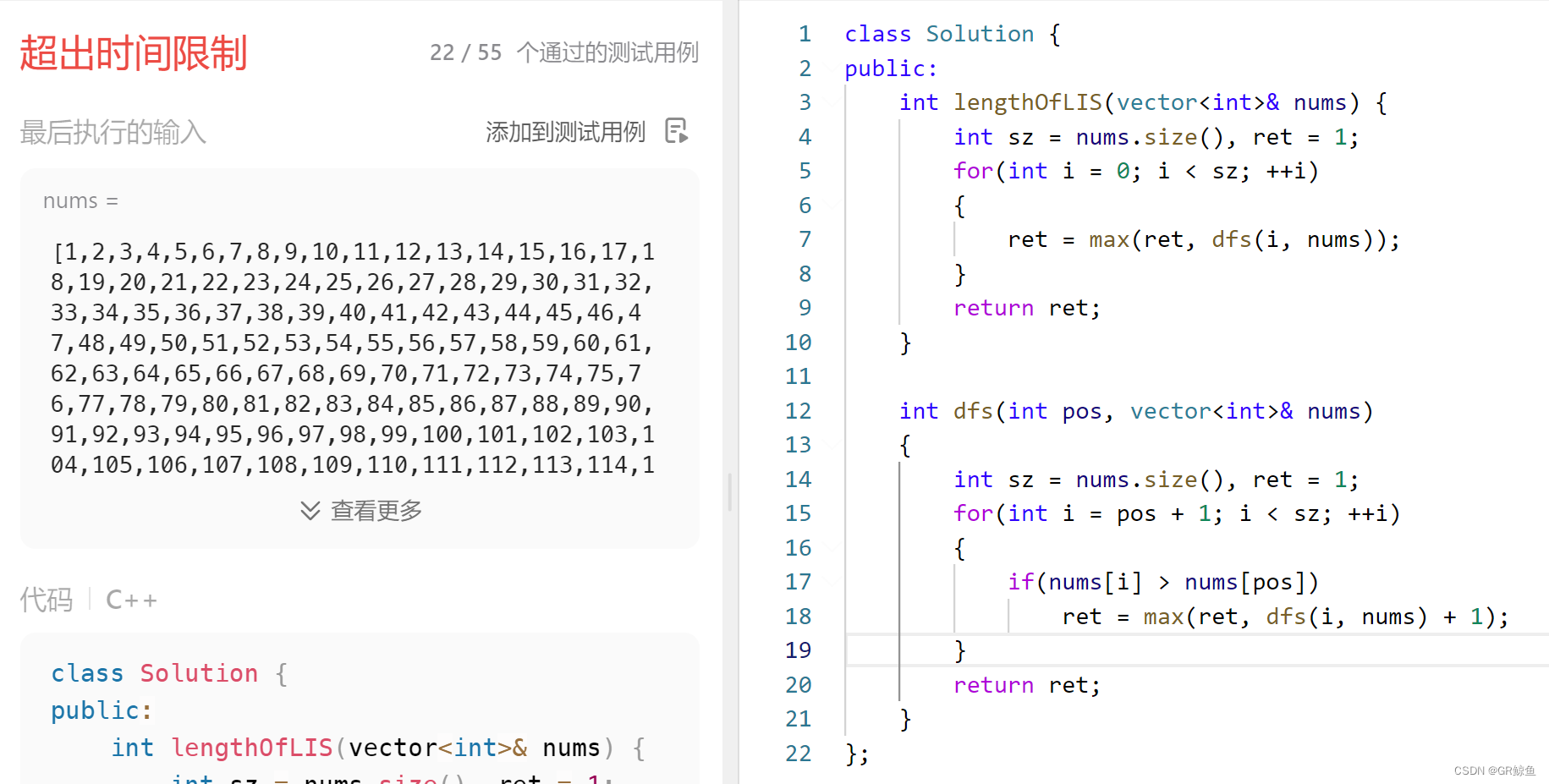
解析代码1_爆搜递归（超时）

  • 递归含义：给 dfs 一个数 i ，返回以 i 位置为起点的最长增子序列的长度。
  • 函数体：遍历 i 后面的所有位置，看谁能加到 i 这个元素的后面。统计所有情况下的最大值。
  • 递归出口：因为是判断之后再进入递归的，因此没有出口。
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int sz = nums.size(), ret = 1;
        for(int i = 0; i < sz; ++i)
        {
            ret = max(ret, dfs(i, nums));
        }
        return ret;
    }

    int dfs(int pos, vector<int>& nums)
    {
        int sz = nums.size(), ret = 1;
        for(int i = pos + 1; i < sz; ++i)
        {
            if(nums[i] > nums[pos])
                ret = max(ret, dfs(i, nums) + 1);
        }
        return ret;
    }
};

解析代码2_记忆化搜索

记忆化搜索解法：

  • 加上一个备忘录。
  • 每次进入递归的时候，去备忘录里面看看。
  • 每次返回的时候，将结果加入到备忘录里面。
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int sz = nums.size(), ret = 1;
        vector<int> memo(sz);
        for(int i = 0; i < sz; ++i)
        {
            ret = max(ret, dfs(i, nums, memo));
        }
        return ret;
    }

    int dfs(int pos, vector<int>& nums, vector<int>& memo)
    {
        if(memo[pos] != 0)
            return memo[pos];
        int sz = nums.size(), ret = 1;
        for(int i = pos + 1; i < sz; ++i)
        {
            if(nums[i] > nums[pos])
                ret = max(ret, dfs(i, nums, memo) + 1);
        }
        memo[pos] = ret;
        return ret;
    }
};

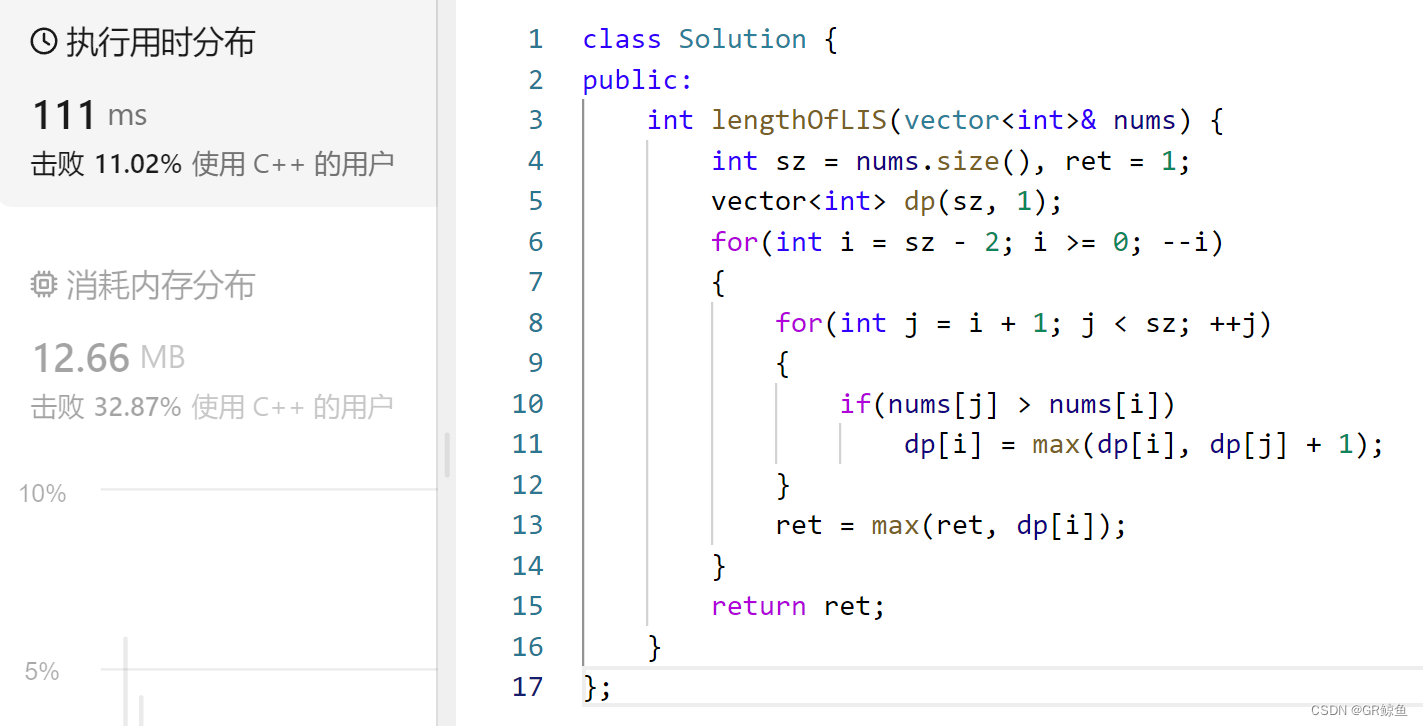
解析代码3_动态规划

根据记忆化搜索得出动态规划的解法：

  • 递归含义：状态表示
  • 函数体：状态转移方程
  • 递归出口：初始化
  • 填表顺序：填备忘录的顺序
  • 返回值：备忘录的值

        注意这里填表顺序有点不一样，因为记忆化搜索填pos位置的值的时候，依赖的是pos后面的值，所以动态规划解法的代码，填表顺序是从后往前填表。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int sz = nums.size(), ret = 1;
        vector<int> dp(sz, 1);
        for(int i = sz - 2; i >= 0; --i)
        {
            for(int j = i + 1; j < sz; ++j)
            {
                if(nums[j] > nums[i])
                    dp[i] = max(dp[i], dp[j] + 1);
            }
            ret = max(ret, dp[i]);
        }
        return ret;
    }
};

④力扣375. 猜数字大小 II

375. 猜数字大小 II

难度 中等

我们正在玩一个猜数游戏，游戏规则如下：

  1. 我从 1 到 n 之间选择一个数字。
  2. 你来猜我选了哪个数字。
  3. 如果你猜到正确的数字，就会 赢得游戏 。
  4. 如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
  5. 每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。

给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数，不管我选择那个数字 。

示例 1：

输入：n = 10
输出：16
解释：制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
        - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
        - 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
        - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
            - 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
            - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
        - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
            - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

示例 2：

输入：n = 1
输出：0
解释：只有一个可能的数字，所以你可以直接猜 1 并赢得游戏，无需支付任何费用。

示例 3：

输入：n = 2
输出：1
解释：有两个可能的数字 1 和 2 。
- 你可以先猜 1 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $1 。
    - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $1 。
最糟糕的情况下，你需要支付 $1 。

提示：

  • 1 <= n <= 200
class Solution {
public:
    int getMoneyAmount(int n) {

    }
};

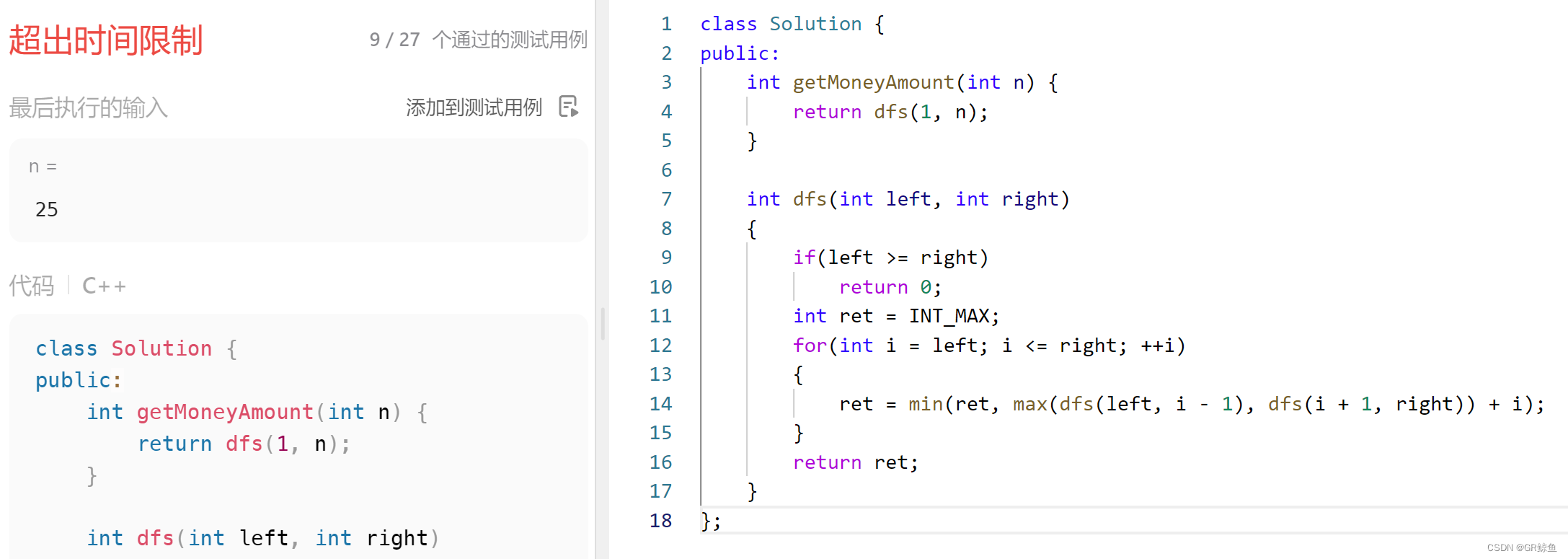
解析代码1_爆搜递归（超时）

  • 递归含义：给 dfs 一个区间 [left, right] ，返回在这个区间上能完胜的最小费用。
  • 函数体：选择 [left, right] 区间上的任意一个数作为头结点，然后递归分析左右子树。 求出所有情况下的最小值。因为要得到这个区间上能完胜的最小费用，所以选择左右子树时要求最大值。
  • 递归出口：当 left >= right 的时候，直接返回 0 。
class Solution {
public:
    int getMoneyAmount(int n) {
        return dfs(1, n);
    }

    int dfs(int left, int right)
    {
        if(left >= right)
            return 0;
        int ret = INT_MAX;
        for(int i = left; i <= right; ++i)
        {
            ret = min(ret, max(dfs(left, i - 1), dfs(i + 1, right)) + i);
        }
        return ret;
    }
};

解析代码2_记忆化搜索

记忆化搜索解法：

  • 加上一个备忘录。
  • 每次进入递归的时候，去备忘录里面看看。
  • 每次返回的时候，将结果加入到备忘录里面。
class Solution {
    int memo[201][201];
public:
    int getMoneyAmount(int n) {
        return dfs(1, n);
    }

    int dfs(int left, int right)
    {
        if(left >= right)
            return 0;
        if(memo[left][right] != 0)
            return memo[left][right];
        int ret = INT_MAX;
        for(int i = left; i <= right; ++i)
        {
            ret = min(ret, max(dfs(left, i - 1), dfs(i + 1, right)) + i);
        }
        memo[left][right] =ret;
        return ret;
    }
};

⑤力扣329. 矩阵中的最长递增路径

329. 矩阵中的最长递增路径

难度 困难

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

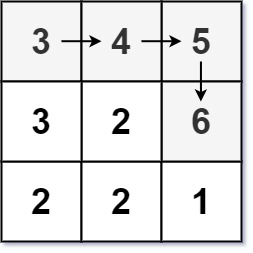
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 200
  • 0 <= matrix[i][j] <= 2^31 - 1
class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {

    }
};

解析代码1_爆搜递归（超时）

  • 递归含义：给 dfs 一个下标 [i, j] ，返回从这个位置开始的最长递增路径的长度。
  • 函数体：上下左右四个方向看一看，哪里能过去就过去，统计四个方向上的最大长度。
  • 递归出口：因为是先判断再进入递归，因此没有出口。
class Solution {
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {1, -1, 0, 0};
    int m = 0, n = 0;
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        m = matrix.size(), n = matrix[0].size();
        int ret = 0;
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                ret = max(ret, dfs(i, j, matrix));
            }
        }
        return ret + 1; // 加上自己
    }

    int dfs(int sr, int sc, vector<vector<int>>& matrix)
    {
        int ret = 0;
        for(int i = 0; i < 4; ++i)
        {
            int x = sr + dx[i], y = sc + dy[i];
            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[sr][sc])
            {
                ret = max(ret, dfs(x, y, matrix) + 1);
            }
        }
        return ret;
    }
};

解析代码2_记忆化搜索

记忆化搜索解法：

  • 加上一个备忘录。
  • 每次进入递归的时候，去备忘录里面看看。
  • 每次返回的时候，将结果加入到备忘录里面。
class Solution {
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {1, -1, 0, 0};
    int m = 0, n = 0;
    int memo[201][201];
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        m = matrix.size(), n = matrix[0].size();
        int ret = 0;
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                ret = max(ret, dfs(i, j, matrix));
            }
        }
        return ret + 1; // 加上自己
    }

    int dfs(int sr, int sc, vector<vector<int>>& matrix)
    {
        if(memo[sr][sc] != 0)
            return memo[sr][sc];
        int ret = 0;
        for(int i = 0; i < 4; ++i)
        {
            int x = sr + dx[i], y = sc + dy[i];
            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[sr][sc])
            {
                ret = max(ret, dfs(x, y, matrix) + 1);
            }
        }
        memo[sr][sc] = ret;
        return ret;
    }
};

本篇完。

下一篇是贪心算法的第四部分。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1657619.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

对时间序列异常检测的严格评价

对时间序列异常检测的严格评价

论文地址&#xff1a;https://ojs.aaai.org/index.php/AAAI/article/view/20680 论文源码&#xff1a;无 会议&#xff1a;The Thirty-Sixth AAAI Conference on Artificial Intelligence 这篇论文名为《Towards a Rigorous Evaluation of Time-Series Anomaly Detection》&a…
阅读更多...
Java毕设之基于SpringBoot的在线拍卖系统

Java毕设之基于SpringBoot的在线拍卖系统

运行环境 开发语言:java 框架:springboot&#xff0c;vue JDK版本:JDK1.8 数据库:mysql5.7(推荐5.7&#xff0c;8.0也可以) 数据库工具:Navicat11 开发软件:idea/eclipse(推荐idea) 系统详细设计 管理员功能模块 管理员登录&#xff0c;管理员通过输入用户名、密码、角色等信…
阅读更多...
网络新手如何上手水牛社软件？我的建议与看法

网络新手如何上手水牛社软件？我的建议与看法

水牛社是一款专为电脑用户设计的软件&#xff0c;拥有明确的著作权&#xff0c;其核心功能在于发布和整合各类网络活动任务资源、教程等&#xff0c;内容多元且不设固定分类。其靠谱程度取决于你对软件的了解程度和个人需求的适配性。 软件内部包含五个主要栏目&#xff0c;大…
阅读更多...
前端开发攻略---打破Chrome的最小字号限制，设置任意字号大小

前端开发攻略---打破Chrome的最小字号限制，设置任意字号大小

目录 1、原因 2、解决方法 1、原因 由于Chrome浏览器的限制&#xff0c;在网页中的字号默认最小为12px&#xff0c;更改为12px以下的字号大小是无效的 2、解决方法 1、在Chrome浏览器中调整字号最小值 优点&#xff1a;快&#xff0c;方便&#xff0c; 缺点&#xff1a;只对自…
阅读更多...
【C++】详解STL容器之一的deque和适配器stack，queue

【C++】详解STL容器之一的deque和适配器stack，queue

目录 deque的概述 deque空间的结构 deque的迭代器 deque的数据设计 deque的优缺点 适配器的概念 ​编辑 stack的概述 stack的模拟实现 queue的概述 queue的模拟实现 deque的概述 deque的设计参考了另外两大容器vector和list。可参考下面两篇文章 详解vector&#x…
阅读更多...
python:画折线图

python:画折线图

import pandas as pd import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties# 设置新宋体字体的路径 font_path D:/reportlab/simsun/simsun.ttf# 加载新宋体字体 prop FontProperties(fnamefont_path)""" # 读取 xlsx 文件 d…
阅读更多...
API低代码平台介绍2-最基本的数据查询功能

API低代码平台介绍2-最基本的数据查询功能

最基本的数据查询功能 本篇文章我们将介绍如何使用ADI平台定义一个基本的数据查询接口。由于是介绍平台具体功能的第一篇文章&#xff0c;里面会涉及比较多的概念介绍&#xff0c;了解了这些概念有助于您阅读后续的文章。 ADI平台的首页面如下&#xff1a; 1.菜单介绍 1.1 O…
阅读更多...
交友软件源码-源码+搭建+售后,上线即可运营聊天交友源码 专业语聊交友app开发+源码搭建-快速上线

交友软件源码-源码+搭建+售后,上线即可运营聊天交友源码 专业语聊交友app开发+源码搭建-快速上线

交友小程序源码是一种可以帮助开发者快速搭建交友类小程序的代码模板。它通常包括用户注册、登录、个人信息编辑、匹配推荐、好友聊天等常见功能&#xff0c;以及与后台数据交互的接口。使用这种源码可以极大地缩短开发时间&#xff0c;同时也可以根据自己的需求进行二次开发和…
阅读更多...
代码随想录算法训练营DAY45|C++动态规划Part7|70.爬楼梯（进阶版）、322. 零钱兑换、279.完全平方数

代码随想录算法训练营DAY45|C++动态规划Part7|70.爬楼梯（进阶版）、322. 零钱兑换、279.完全平方数

文章目录 70.爬楼梯&#xff08;进阶版&#xff09;⭐️322. 零钱兑换思路CPP代码总结 279.完全平方数思路CPP代码 70.爬楼梯&#xff08;进阶版&#xff09; 卡码网&#xff1a;57. 爬楼梯 文章讲解&#xff1a;70.爬楼梯(进阶版) 本题就是典型了完全背包排列问题&#xff0c;…
阅读更多...
光峰科技2023年营收、净利润均双位数下滑，新一年延续？

光峰科技2023年营收、净利润均双位数下滑，新一年延续？

近日&#xff0c;深圳光峰科技股份有限公司&#xff08;688007.SH&#xff0c;下称“光峰科技”&#xff09;对外公布了2023年和2024年一季度的经营“成绩单”。 透视财报不难看出&#xff0c;虽然光峰科技在降低成本、提振销售等层面下足了功夫&#xff0c;但受制于市场需求式…
阅读更多...
交易复盘-20240509

交易复盘-20240509

仅用于记录当天的市场情况&#xff0c;用于统计交易策略的适用情况&#xff0c;以便程序回测 短线核心&#xff1a;不参与任何级别的调整&#xff0c;采用龙空龙模式 一支股票 10%的时候可以操作&#xff0c; 90%的时间适合空仓等待 百合花 (4)|[9:25]|[17717万]|1.93 时代万恒…
阅读更多...
【SpringBoot记录】自动配置原理（1）：依赖管理

【SpringBoot记录】自动配置原理（1）：依赖管理

前言 我们都知道SpringBoot能快速创建Spring应用&#xff0c;其核心优势就在于自动配置功能&#xff0c;它通过一系列的约定和内置的配置来减少开发者手动配置的工作。下面通过最简单的案例分析SpringBoot的功能特性&#xff0c;了解自动配置原理。 SpringBoot简单案例 根据S…
阅读更多...
5.9gunplot绘图堆叠柱状图

5.9gunplot绘图堆叠柱状图

gunplot绘图堆叠柱状图 plot"要用的数据&#xff08;后缀名是.dat)" using 2 t(或者title) 跟着是要命名的属性名称 这个名称可以用.dat里的每列列名&#xff0c;也可以直接在后面跟着定义 plot "data.dat" using 2 t columnheader(2), using 3 t column…
阅读更多...
【websocket-客户端可视化工具】

【websocket-客户端可视化工具】

postman 新版postman (版本v11以上) &#xff0c;除了http协议&#xff0c;还支持了Websocket&#xff0c;MQTT&#xff0c;gRPC等多种连接协议&#xff0c;可以作为多种协议的客户端&#xff0c;使用起来非常方便。 使用 服务端代码 这里以websocket协议举例&#xff0c;代…
阅读更多...
2023-2024年家电行业报告合集（精选51份）

2023-2024年家电行业报告合集（精选51份）

家电行业报告/方案&#xff08;精选51份&#xff09; 2023-2024年 报告来源&#xff1a;2023-2024年家电行业报告合集&#xff08;精选51份&#xff09; 【以下是资料目录】 空气炸锅出海品牌策划创意全案【家电出海】【品牌全案】 卡萨帝潮流消费品生活家电音乐节活动方案…
阅读更多...
【Python】了解卡方检验方法及其应用

【Python】了解卡方检验方法及其应用

是否幸福轻得太沉重 过度使用不痒不痛 烂熟透红空洞了的瞳孔 终于掏空终于有始无终 得不到的永远在骚动 被偏爱的都有恃无恐 玫瑰的红容易受伤的梦 握在手中却流失于指缝 又落空 &#x1f3b5; 陈奕迅《红玫瑰》 卡方检验&#xff08;Chi-square test&…
阅读更多...
大数据手册(Spark)--Spark 简介

大数据手册(Spark)--Spark 简介

Spark 简介 Apache Spark 是一种用于大数据工作负载的分布式开源处理系统。它使用内存中缓存和优化的查询执行方式&#xff0c;可针对任何规模的数据进行快速分析查询。Apache Spark 提供了简明、一致的 Java、Scala、Python 和 R 应用程序编程接口 (API)。 Apache Spark 是专…
阅读更多...
Java毕设之基于springboot的医护人员排班系统

Java毕设之基于springboot的医护人员排班系统

运行环境 开发语言:java 框架:springboot&#xff0c;vue JDK版本:JDK1.8 数据库:mysql5.7(推荐5.7&#xff0c;8.0也可以) 数据库工具:Navicat11 开发软件:idea/eclipse(推荐idea) 系统详细实现 医护类型管理 医护人员排班系统的系统管理员可以对医护类型添加修改删除以及…
阅读更多...
[Linux深度学习笔记5.9]

[Linux深度学习笔记5.9]

5.9笔记 DNS: 软硬链接&#xff1a; 软链接&#xff1a; 软链接&#xff1a;ln -s /源文件 /目标位置/链接名称》创建软链接1.既可以对目录使用&#xff0c;也可以对文件使用2.删除源文件&#xff0c;软链接不可用3.软链接可以跨文件系统使用4.源文件和软链接的inode号不同5.…
阅读更多...
Baidu Comate智能编码助手：大学生的代码编写助手

Baidu Comate智能编码助手：大学生的代码编写助手

Baidu Comate智能编码助手&#xff1a;大学生的代码编写助手 前言一、关于Baidu Comate智能编码助手1.1 Baidu Comate智能编码助手简介1.2 产品功能 二、安装使用&#xff08;本文以pycharm为例&#xff09;三、我的百度Comate之旅3.1智能推荐3.1.1 单行推荐3.1.2 多行推荐 3.2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023