【python】基于岭回归算法对学生成绩进行预测

news2024/11/20 22:39:03

前言

在数据分析和机器学习领域，回归分析是一种预测连续数值的监督学习技术。当数据特征与目标变量之间存在线性关系时，线性回归模型尤其有用。然而，当特征数量多于样本数量，或者特征之间存在多重共线性时，普通最小二乘法可能不是最佳选择。这时，岭回归（Ridge Regression）作为一种改进的线性回归方法，通过引入正则化项来防止模型过拟合，从而提高模型的泛化能力。

正文

数据加载与预处理

在本例中，我们使用pandas库加载了一个名为data.csv的数据集。数据集被分为特征集X和目标变量y。为了简化问题，我们只取前两列作为特征，并假设第三列是目标变量。

data = pd.read_csv('data.csv')
X = data.iloc[:, :2]  # 取前两列作为特征
y = data.iloc[:, 2]  # 取第三列作为目标变量

接下来，我们使用train_test_split函数将数据集分为训练集和测试集，其中测试集占20%。这样做的目的是为了在模型训练完成后，能够在未见过的数据上评估模型性能。

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

在进行模型训练之前，对特征进行标准化是很重要的。这可以通过StandardScaler实现，它将数据缩放到均值为0，标准差为1。

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

模型选择与超参数优化

岭回归是一种通过引入L2正则化项来防止模型过拟合的线性回归方法。正则化项的强度由超参数alpha控制。为了找到最佳的alpha值，我们使用GridSearchCV进行超参数优化。

alpha_candidates = [1e-15, 1e-10, 1e-5, 1e-2, 1, 5, 10, 20]
grid_search = GridSearchCV(estimator=ridge, param_grid={'alpha': alpha_candidates}, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(X_train_scaled, y_train)

GridSearchCV通过交叉验证的方式在给定的参数网格中寻找最佳的参数组合。我们选择了5折交叉验证，并使用负均方误差作为评分指标，因为GridSearchCV默认寻找评分指标的最大值，而均方误差越小越好。

模型训练与评估

在找到最佳的alpha值后，我们使用这个值来训练最终的岭回归模型，并在测试集上进行预测。

best_alpha = grid_search.best_params_['alpha']
ridge_best = Ridge(alpha=best_alpha)
ridge_best.fit(X_train_scaled, y_train)
y_pred = ridge_best.predict(X_test_scaled)

为了评估模型性能，我们计算了均方误差（MSE），这是一个常用的回归评估指标。

mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error with best alpha: {mse}')

结果可视化

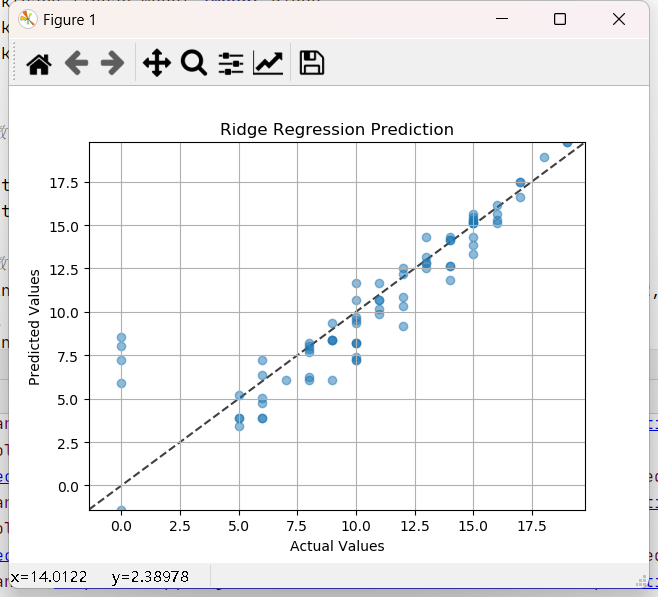
最后，我们通过绘制实际值与预测值的散点图来可视化模型的预测效果。理想情况下，预测值应该与实际值完全一致，即所有点都落在对角线上。

plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Ridge Regression Prediction')
plt.plot(lims, lims, 'k--', alpha=0.75, zorder=0)
plt.grid(True)
plt.show()

通过散点图，我们可以直观地看到模型的预测效果。如果大多数点都集中在对角线附近，那么模型的预测效果就比较好。
在这里插入图片描述

总结

本文介绍了如何使用岭回归模型对数据集进行分析，并展示了如何通过超参数优化来提高模型性能。其中使用了GridSearchCV来寻找最佳的alpha值，并使用均方误差作为评估指标。最后，我们通过可视化手段直观地展示了模型的预测效果。岭回归作为一种有效的正则化方法，在处理特征数量多或存在多重共线性的数据集时，能够提高模型的泛化能力。

整体代码

import pandas as pd
import numpy as np
from sklearn.model_se`在这里插入代码片`lection import train_test_split, GridSearchCV
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# 1. 数据加载
data = pd.read_csv('data.csv')
X = data.iloc[:, :2]  # 取前两列作为特征
y = data.iloc[:, 2]  # 取第三列作为目标变量

# 2. 数据预处理
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 3. 使用GridSearchCV来优化alpha值
# 定义alpha值的候选范围
alpha_candidates = [1e-15, 1e-10, 1e-5, 1e-2, 1, 5, 10, 20]

# 创建岭回归模型
ridge = Ridge()

# 创建GridSearchCV对象
grid_search = GridSearchCV(estimator=ridge, param_grid={'alpha': alpha_candidates}, cv=5,
                           scoring='neg_mean_squared_error')

# 执行网格搜索
grid_search.fit(X_train_scaled, y_train)

# 获取最佳alpha值
best_alpha = grid_search.best_params_['alpha']
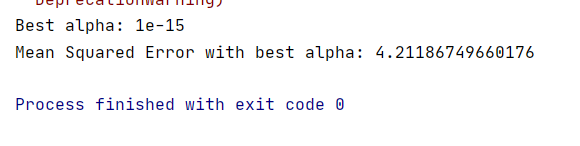
print(f"Best alpha: {best_alpha}")

# 使用最佳alpha值训练模型
ridge_best = Ridge(alpha=best_alpha)
ridge_best.fit(X_train_scaled, y_train)

# 进行预测
y_pred = ridge_best.predict(X_test_scaled)

# 评估模型
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error with best alpha: {mse}')

# 注意：这里使用的是负均方误差作为评分指标，因为GridSearchCV默认寻找最大值，而均方误差越小越好，所以取负值。

# 4. 可视化预测结果
plt.scatter(y_test, y_pred, alpha=0.5)  # 绘制实际值与预测值的散点图
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Ridge Regression Prediction')

# 绘制理想情况的对角线
lims = [
    np.min([y_test.min(), y_pred.min()]),  # x轴最小值
    np.max([y_test.max(), y_pred.max()]),  # x轴最大值
]
plt.plot(lims, lims, 'k--', alpha=0.75, zorder=0)
plt.xlim(lims)
plt.ylim(lims)

# 显示图形
plt.grid(True)
plt.show()