48. 旋转图像
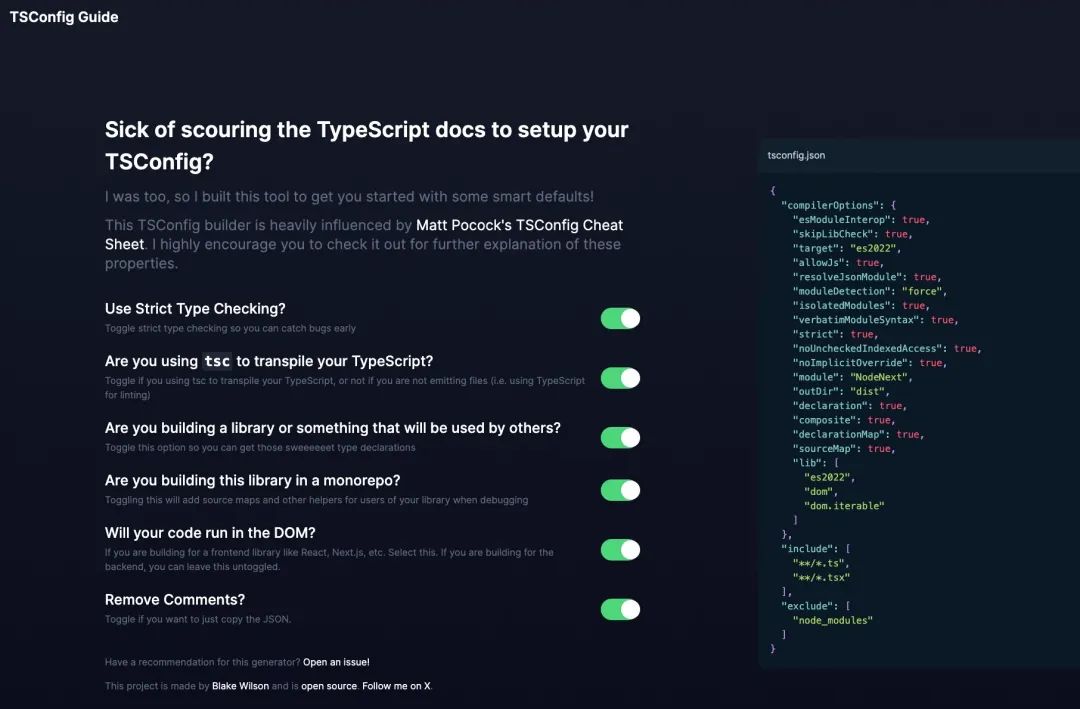
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 :
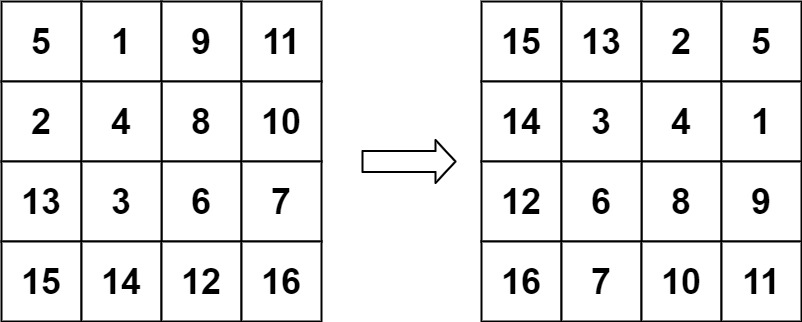
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
思路:
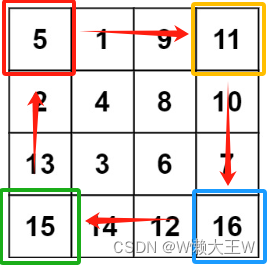
以i=0,j=0元素5开始,旋转过程中的交替顺序就是5->11->16->15->5
元素位置的行和列变化:[0][0]->[0][3]->[3][3]->[3][0]->[0][0]
以元素1为例:1->10->12->13->1
元素位置的行和列变化:[0][1]->[1][3]->[3][2]->[2][0]->[0][1]
以元素9为例:9->7->14->2->9
元素位置的行和列变化:[0][2]->[2][3]->[3][1]->[1][0]->[0][2]
抽象成i和j的变化:[i][j]->[j][n-1-i]->[n-1-i][n-1-j]->[n-1-j][i]->[i][j]
转换成核心代码:注意需要一个临时变量去存储起点的值,防止覆盖以后不知道旋转后的位置填入什么,当然这个临时变量也可以存储终点的值,最后填入起点也是可以的,就是代码顺序变一下
int temp=matrix[i][j];
matrix[i][j]=matrix[n-j-1][i];
matrix[n-j-1][i]=matrix[n-i-1][n-j-1];
matrix[n-i-1][n-j-1]=matrix[j][n-i-1];
matrix[j][n-i-1]=temp;到此最外圈已经处理完成,不妨确定一下终止条件:三个起点,5,1,9它们i=0,j递增,j一开始等于i,最后小于n-1-i。(可以通过6X6的矩阵验证,黄色是每圈的起点,红色是每圈的终点)

加上之前的核心代码:
for(int j=i;j<n-i-1;j++){
int temp=matrix[i][j];
matrix[i][j]=matrix[n-j-1][i];
matrix[n-j-1][i]=matrix[n-i-1][n-j-1];
matrix[n-i-1][n-j-1]=matrix[j][n-i-1];
matrix[j][n-i-1]=temp;
}最后就是处理圈由外向内收缩的过程,通过6X6的矩阵,可以看到圈数是3,5X5的矩阵圈数也是3,所以圈数=n/2,i从0开始,递增。
代码:
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n=matrix.size();
for(int i=0;i<n/2;i++){
for(int j=i;j<n-i-1;j++){
int temp=matrix[i][j];
matrix[i][j]=matrix[n-j-1][i];
matrix[n-j-1][i]=matrix[n-i-1][n-j-1];
matrix[n-i-1][n-j-1]=matrix[j][n-i-1];
matrix[j][n-i-1]=temp;
}
}
}
};240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
思路:暴力可以直接两层循环解出来,这里利用矩阵升序和降序的特点写出解法
我们可以模仿爬虫,对于目标数,如果当前处在的元素大于目标数,我们就向降序的方向移动;如果当前处在的元素小于目标数,我们就向升序的方向移动。这就是爬虫选择方向的规则。
我们现在确定爬虫的起点,左上,左下,右上,右下
左上向右,向下都是升序;右下向上,向左都是升序,不作为爬虫的起点。
左下向右升序,向上降序;右上向左降序,向下升序,可以作为爬虫起点。
我们以左下为起点,开始搜索目标值5,18>5向上爬,10>5向上爬,3<5向右爬,6>5向上爬,找到返回true。

代码:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int i=matrix.size()-1;
int j=0;
while(i>=0&&j<matrix[0].size()){
if(matrix[i][j]>target) i--;//向上爬
else if(matrix[i][j]<target) j++;//向右爬
else return true;
}
return false;
}
};
![[Kubernetes] sealos部署 K8s 集群](https://img-blog.csdnimg.cn/direct/485bb6dbead64719a9f011cbf56d07df.png)