💓博主CSDN主页:杭电码农-NEO💓
⏩专栏分类:高阶数据结构专栏⏪
🚚代码仓库:NEO的学习日记🚚
🌹关注我🫵带你学习更多Go语言知识
🔝🔝

高阶数据结构
- 1. 前言
- 2. 图的基本概念
- 3. 关于图的专业名词
- 4. 图的存储结构
- 4.1 邻接矩阵
- 4.2 邻接表
- 4.3 优缺点分析
- 5. 图的模拟实现
- 6. 总结以及拓展
1. 前言
相信在大学中学过离散数学这门课的同学一定对图比较熟悉. 为了照顾没有学习过图的同学,本系列文章会当作无基础来讲解
本章重点:
本篇文章着重讲解图的基本概念,关于图的一些专业名词,以及图的两个存储结构: 邻接矩阵和邻接表. 期间会带大家模拟实现邻接矩阵版本的图
2. 图的基本概念
图是由顶点集合,以及边集合组成的一种数据结构: G = (V,E).

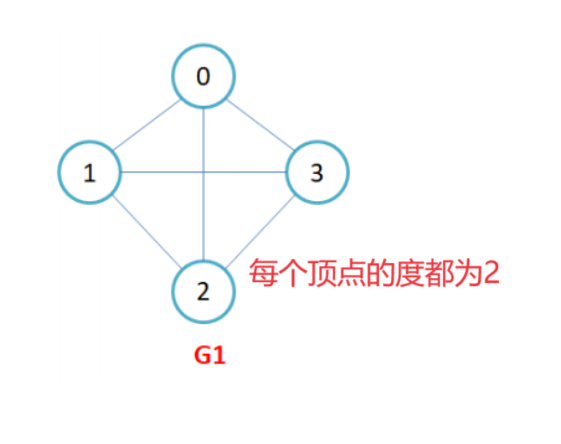
概念很抽象,可以简化为下图:
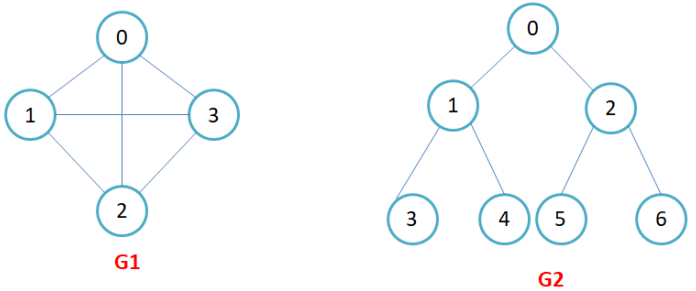
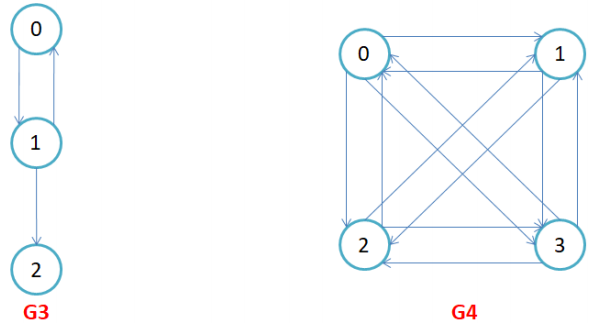
G1中的顶点就是结点0,1,2,3.记作v1,v2…,两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边,图中的第k条边记作ek,ek = (vi,vj)或<vi,vj>. 再看G2,这不是一颗二叉树吗?是的,可以将二叉想象为图的一种表现形式. 除此之外, 图还分为有向图和无向图, 有向图代表顶点之间的边是有方向的, 无向图代表边是无方向的,如下图所示:
3. 关于图的专业名词
完全图:在有n个顶点的无向图中,若有n * (n-1)/2条边,即任意两个顶点之间有且仅有一条边,则称此图为无向完全图. 上图的G1就是无向完全图, G4为有向完全图邻接顶点:若顶点u和v有直接的边相连, 那么它们这两个顶点就称为邻接顶点顶点的度:顶点v的度是它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。注意:对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。
路径:若顶点A可以到达顶点B, 则从A到B经过的所有顶点就是A到B的路径. 对于不带权图,路径长度等于边数之和,带权图则是权值之和
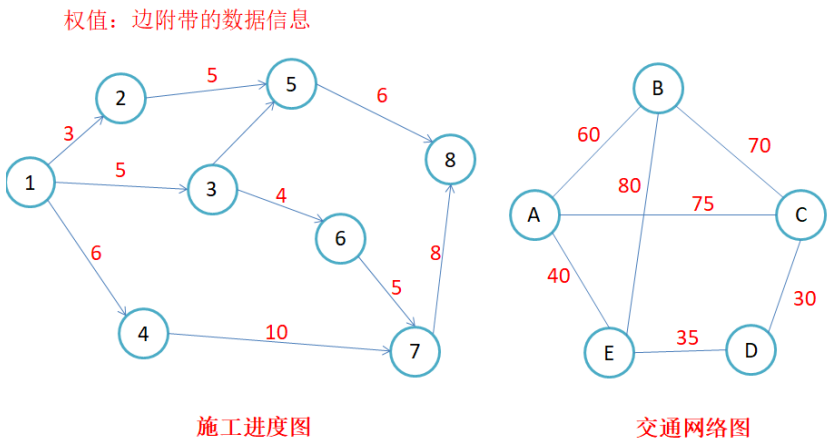
简单路径与回路:一条路径中如果没有重复的点,那么就是简单路径,有重复的点证明有回路连通图:连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图
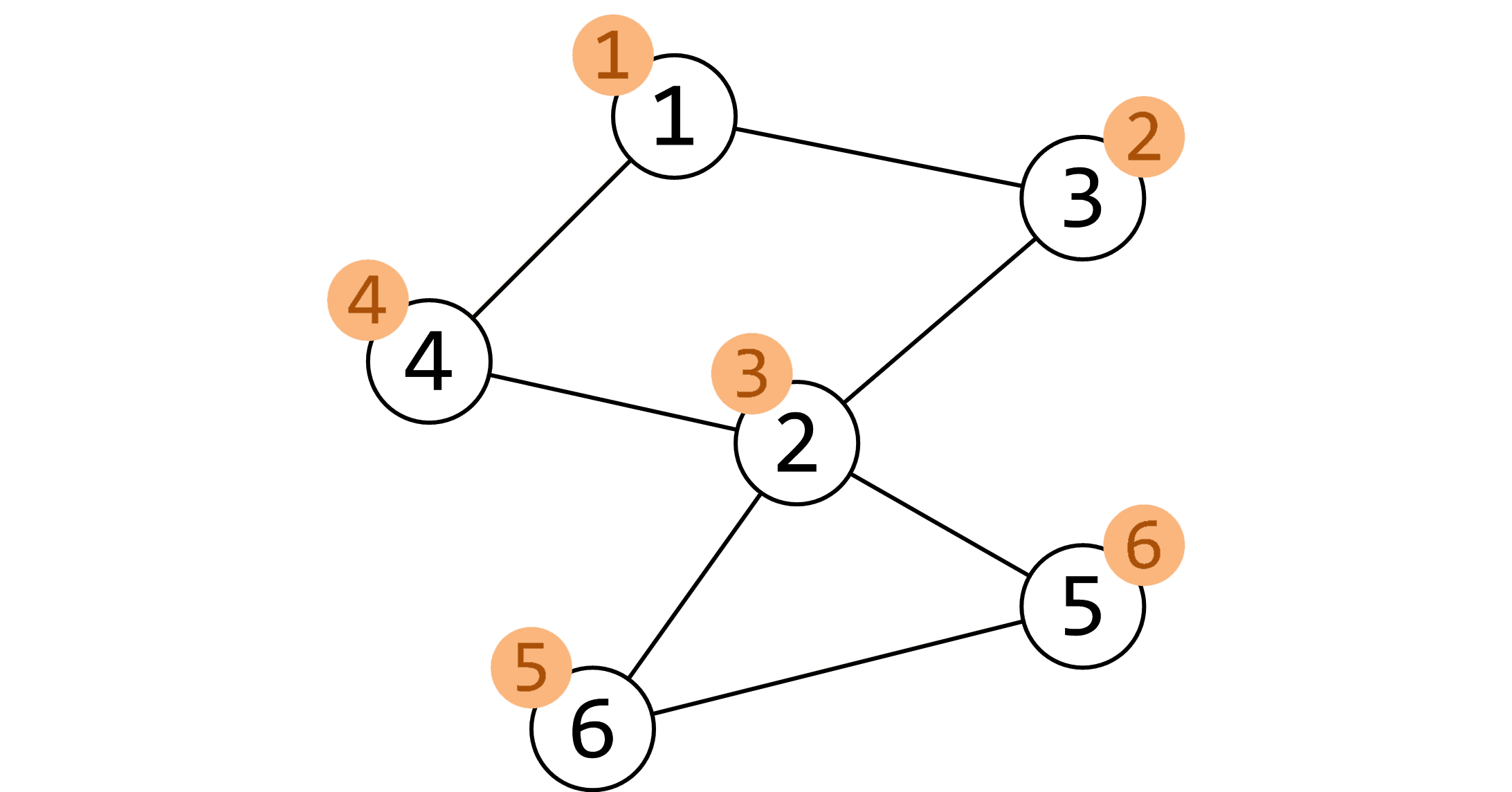
这些概念很多,很杂,不用全部背下来, 有个印象,后面使用时不至于听不懂就好了.可以联想到, 微信,QQ等社交平台一定是无向图,因为我是你好友的同时你必须也得是我好友.像抖音,快手,微博这种弱社交平台, 用的是有向图, 因为我关注了一个博主并不代表这个博主也要关注我
4. 图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边关系即可。节点保存比较简单,只需要一个数组存储即可,那边关系该怎么保存呢?
图的存储结构分为:
- 邻接矩阵
- 邻接表
4.1 邻接矩阵
因为节点与节点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系. 如一个图有n个顶点, 那么就开辟一个n×n的二维数组. 数组下标(i,j)位置存储的值代表,顶点i到j是否有边,用0/1表示.
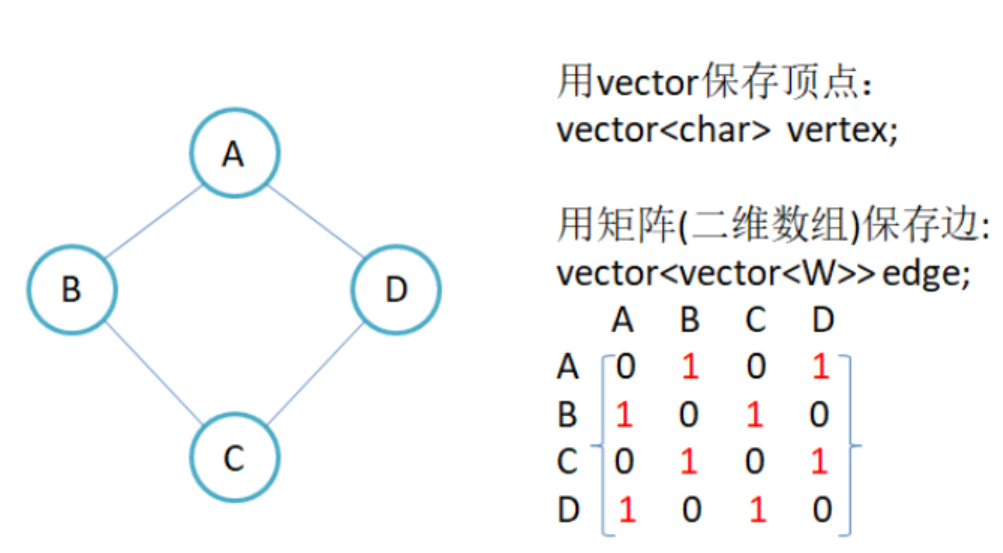
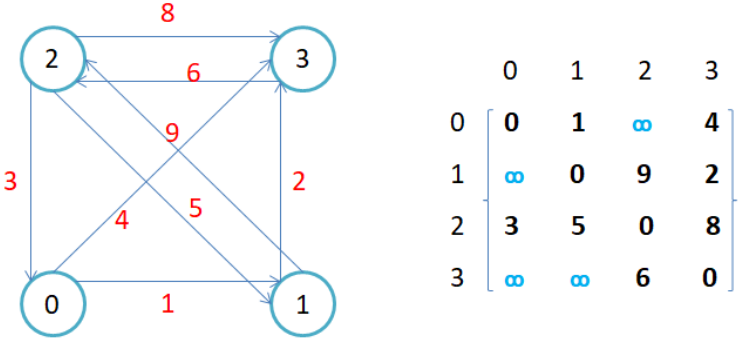
对于无向图而言, 邻接矩阵是对称的,因为我有边到你的同时,你也一定有边到我. 但是对于有向图而言,就不是这么简单了,下面来看看

如果边带有权值,并且两个节点之间是连通的,上图中的边的关系就用权值代替,如果两个顶点不通,则使用无穷大代替
4.2 邻接表
邻接表: 用数组表示顶点的集合,用链表表示边的关系
无向图邻接表存储:
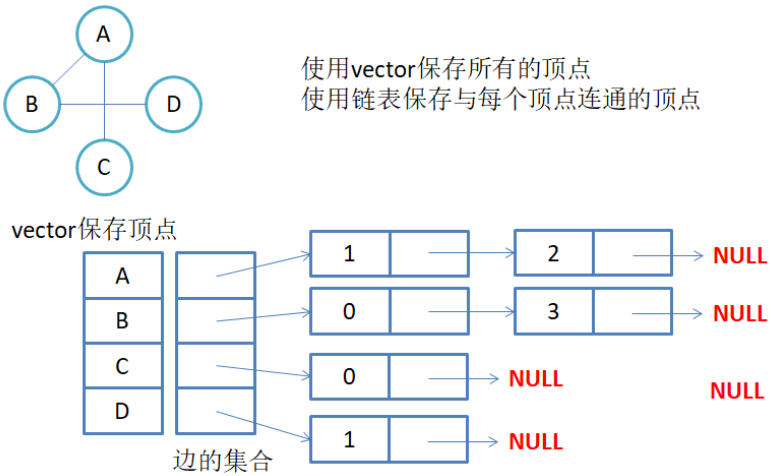
A,B,C,D的下标分别是0,1,2,3.所以A顶点有两个相邻的顶点B和C. 链表中存的就是1,2
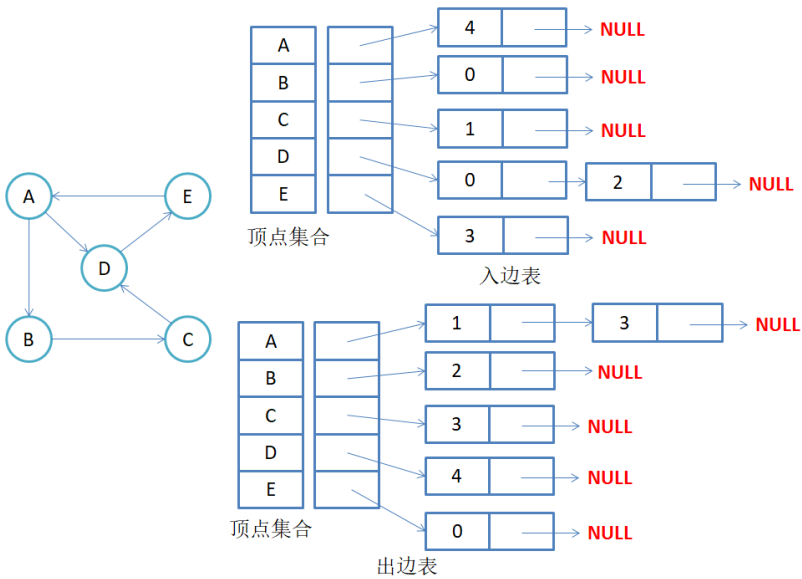
有向图邻接表存储:
4.3 优缺点分析
用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通,缺陷是如果顶点比较多,边比较少时,矩阵中存储了大量的0成为系数矩阵,比较浪费空间,并且要求两个节点之间的路径不是很好求。
而邻接表的优点是很快能判断出一个顶点与哪些顶点直接相连. 而邻接表想要知道两个顶点是否连通,要比邻接矩阵要麻烦
5. 图的模拟实现
首先, 使用邻接矩阵版本的图, 需要一个一维数组来存储顶点的集合, 需要一个二维数组来存储边的集合. 除此之外, 由于我们全程使用的是顶点的下标, 所以还需要一个map来存储顶点下标和顶点的值的对应关系.
框架代码:
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
//图的创建方法: 1. IO输入(不方便测试) 2. 样例写在文件中,读取文件 3. 手动添加边
Graph(const V* a,size_t n)
{
_vertex.reserve(n);
for (int i = 0; i < n; i++)
{
_vertex.push_back(a[i]);
_index[a[i]] = i;
}
_edge.resize(n);
for (int i = 0; i < n; i++)
_edge[i].resize(n, MAX_W);
}
private:
vector<V> _vertex; //图的顶点集合
vector<vector<W>> _edge;//图的边的集合
unordered_map<V, int> _index;//存储顶点和它映射到vector的下标的关系
};
代码中的模板参数V代表顶点的类型,W代表边的类型(可能是整数,bool甚至是字符串),而MAX_W将作为边集合,二维数组的初始值. 最后一个代表,是否为有向图. 除此之外,图中还应该实现几个基本的函数: 添加边, 打印图的内容
完整的代码:
//邻接矩阵版本
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
//图的创建方法: 1. IO输入(不方便测试) 2. 样例写在文件中,读取文件 3. 手动添加边
Graph(const V* a,size_t n)
{
_vertex.reserve(n);
for (int i = 0; i < n; i++)
{
_vertex.push_back(a[i]);
_index[a[i]] = i;
}
_edge.resize(n);
for (int i = 0; i < n; i++)
_edge[i].resize(n, MAX_W);
}
//找到顶点对应的下标
size_t GetIndex(const V& v)
{
if (_index.find(v) == _index.end())
{
cout << "要添加的边的顶点不存在" << endl;
return -1;
}
return _index[v];
}
void AddEdge(const V& src, const V& dest, const W& w)//向图中添加边(源点,目标点,以及权值)
{
size_t srci = GetIndex(src);
size_t desti = GetIndex(dest);
_edge[srci][desti] = w;
if (Direction == false)
_edge[desti][srci] = w;
}
void Print()
{
//打印顶点
for (int i = 0; i < _edge[0].size(); i++)
cout << "[" << i << "]" << "->" << _vertex[i] << endl;
cout << endl;
//打印矩阵
for (int i = 0; i < _edge[0].size(); i++)
{
for (int j = 0; j < _edge[0].size(); j++)
{
if (_edge[i][j] == MAX_W)
cout << "* ";
else cout << _edge[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
private:
vector<V> _vertex; //图的顶点集合
vector<vector<W>> _edge;//图的边的集合
unordered_map<V, int> _index;//存储顶点和它映射到vector的下标的关系
};
void TestGraph()
{
Graph<char, int, -1, true> g("0123", 4);
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
g.Print();
}
6. 总结以及拓展
其实模拟实现图的意义并不是简单的实现添加边的函数. 而是为了后面关于图的各种算法做铺垫. 图的学习难度会越来越大, 加油吧, 少年.