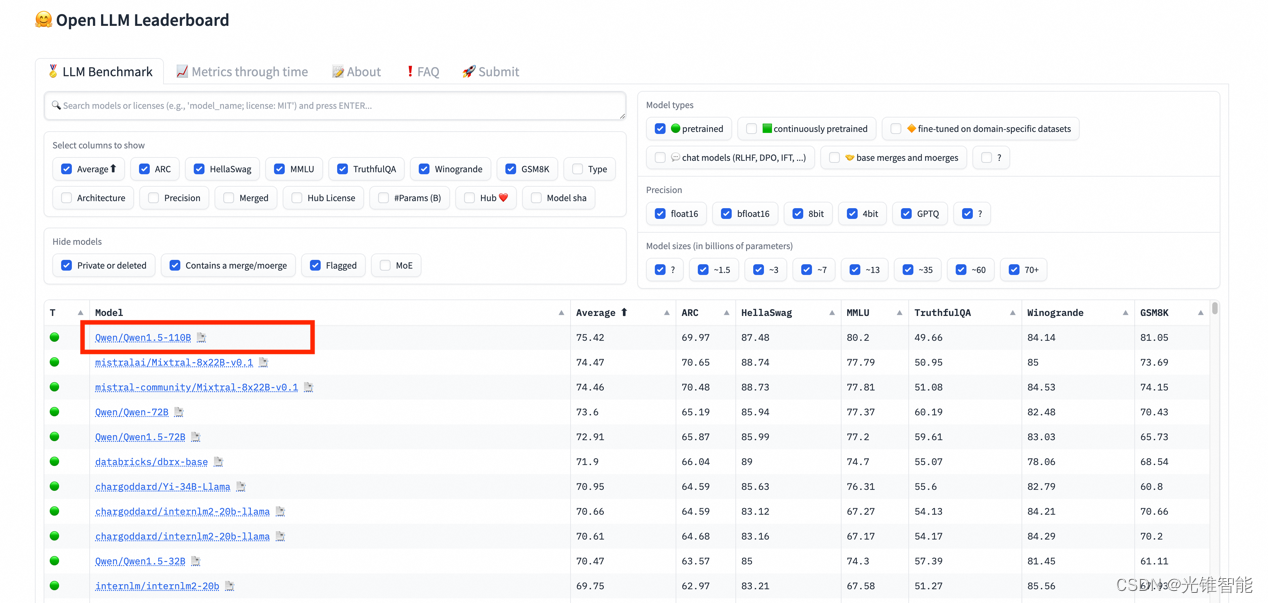
在OpenCV中处理从表格切割下来的图片,并去掉单元格的边框线,以提升Tesseract的识别准确率,确实是一个具有挑战性的任务。在这种情况下,我们需要采取一种策略来预处理图像,使得数字与背景之间的对比度增强,同时减少或消除边框线的影响。
一种可能的方法是尝试结合图像处理和机器视觉技术,通过以下步骤来实现:
1. **图像预处理**:首先,对图像进行预处理,以减少噪声和增强对比度。这可能包括灰度化、二值化、去噪等操作。使用`cv2.cvtColor`函数将图像转换为灰度图像,然后可以使用`cv2.threshold`或`cv2.adaptiveThreshold`进行二值化处理。此外,`cv2.medianBlur`或`cv2.GaussianBlur`可用于去除噪声。
2. **边缘检测**:虽然Canny边缘检测算法在一般情况下表现良好,但在处理表格边框时可能会遇到困难。可以尝试调整Canny算法的阈值参数(`threshold1`和`threshold2`),或者尝试使用其他边缘检测算法,如Sobel、Laplacian或Scharr,看看是否能得到更好的结果。
3. **轮廓查找和筛选**:使用`cv2.findContours`函数找到图像中的轮廓。然后,根据轮廓的大小、形状或其他特征来筛选掉表格边框的轮廓。这可能需要一些实验和调整,以找到最佳的筛选条件。
4. **填充轮廓**:对于筛选后保留的轮廓(即认为是数字部分的轮廓),可以使用`cv2.drawContours`函数和`cv2.fillPoly`函数来填充这些轮廓,从而去除边框线的影响。
5. **后处理**:在填充轮廓后,可能还需要进行一些后处理操作,如形态学操作(腐蚀、膨胀)、连通域分析等,以进一步改进数字与背景之间的对比度。
6. **Tesseract识别**:在完成上述预处理步骤后,将处理后的图像输入给Tesseract进行识别。此时,由于已经去除了边框线的影响,并增强了数字与背景之间的对比度,Tesseract的识别准确率应该会有所提升。
需要注意的是,这个过程可能需要根据具体的图像和识别需求进行调整和优化。此外,由于表格边框和数字可能具有相似的颜色或纹理特征,完全去除边框线而不影响数字识别可能是一个具有挑战性的任务。因此,可能需要尝试不同的方法和技术,以找到最适合的解决方案。
发布于:广东省